Метод прямоугольников

Пусть требуется определить значение интеграла функции на отрезке 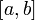. Этот отрезок делится точками 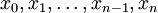на 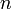равных отрезков длиной 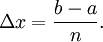Обозначим через 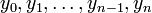значение функции 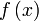в точках 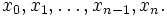Далее составляем суммы 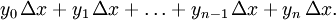Каждая из сумм — интегральная сумма для 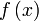на 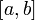и поэтому приближённо выражает интеграл

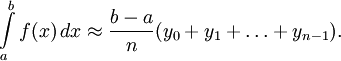
Если заданная функция — положительная и возрастающая, то эта формула выражает площадь ступенчатой фигуры, составленной из «входящих» прямоугольников, также называемая формулой левых прямоугольников, а формула

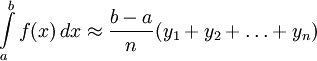
выражает площадь ступенчатой фигуры, состоящей из «выходящих» прямоугольников, также называемая формулой правых прямоугольников. Чем меньше длина отрезков, на которые делится отрезок 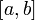, тем точнее значение, вычисляемое по этой формуле, искомого интеграла.

Очевидно, стоит рассчитывать на бо́льшую точность если брать в качестве опорной точки для нахождения высоты точку посередине промежутка. В результате получаем формулу средних прямоугольников: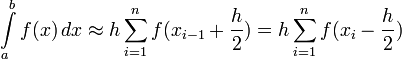

где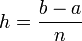

Учитывая априорно бо́льшую точность последней формулы при том же объеме и характере вычислений её называют формулой прямоугольников