Множественная регрессия

Изучение связи между тремя и более связанными между собой признаками носит название множественной (многофакторной) регрессии. При исследовании зависимостей методами множественной регрессии требуется определить аналитическое выражение связи между результативным признаков (Y) и множеством факторных признаков (x₁, x₂, x₃,…x_n).

Построение моделей множественной регрессии включает несколько этапов:

· выбор формы связи (уравнения регрессии);

· отбор факторных признаков;

· обеспечение достаточного объема совокупности для получения реальных оценок.

Практика построения многофакторных моделей показывает, что все реально существующие зависимости между социально-экономическими явлениями можно описать, используя пять типов моделей:

· линейная;

· степенная;

· показательная;

· параболическая;

· гиперболическая.

Качество уравнения регрессии зависит от степени достоверности и надежности исходных данных и объема совокупности.

Немаловажное значение имеет процедура отбора факторов в уравнение. Наиболее приемлемым способом отбора факторных признаков является шаговая регрессия. Сущность метода шаговой регрессии заключается в последовательном включении факторов в уравнение регрессии и последующей проверке их значимости.

Если при включении нового фактора в модель, коэффициенты регрессии меняют не только свои значения, но и знаки, а множественный коэффициент корреляции не возрастает, то данный факторный признак признается нецелесообразным для включения в модель связи.

Сложность и взаимно переплетение отдельных факторов, обуславливающих исследуемое экономическое явление, могу проявляться в так называемой мультиколлинеарности. Под мультиколлинеарностью понимается тесная зависимость между факторными признаками, включенными в модель. Одним из индикаторов определения мультиколлинеарности между признаками является превышение парным коэффициентом корреляции величины 0,8.

При наличии линейной связи между результативным и несколькими факторными признака, а также между парой факторных признаков определяется множественный коэффициент корреляции:

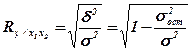
Множественный коэффициент корреляции изменяется в пределах от 0 до 1. Чем ближе R к единице свидетельствует о сильной зависимости между признаками.

Рекомендуемая литература

Основная литература:

Рекомендовано Министерством образования РФ

1. Ефимова М.Р. Общая теория статистики. – М.: Финансы и статистика, 2006.

2. Ефимова М.Р. Сборник задач по общей теории статистики. – М.: Финансы и статистика, 2005.

3. Практикум по теории статистики / Под ред. Шмойловой Р.А., – М.: Финансы и статистика, 2006.

4. Теория статистики / Под ред. Шмойловой Р.А., – М.: Финансы и статистика, 2006.

Дополнительная литература:

1. Сборник задач по общей теории статистики / Под ред. Глинского Н.Н. – М.: Инфра-М, 2000.

2. Статистика. Курс лекций / Под ред. Ионина И.Г.- М.: Инфра-М, Новосибирск: изд-во НГУ,2003.

[1] Теория статистики / Под ред. Р.А. Шмойловой. М.: Финансы и статистика, 2006.