В случае линейной зависимости между двумя коррелируемыми величинами тесноту связи измеряют линейным коэффициентом корреляции (r), который может быть рассчитан по нескольким формулам:
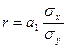
| (10.5) |
где а1- коэффициент регрессии в уравнении связи;
σх- среднее квадратическое отклонение факторного признака;
σу- среднее квадратическое отклонение результативного признака.
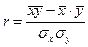
| (10.6) |
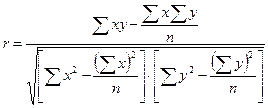
| (10.7) |
Линейный коэффициент корреляции может принимать значения от -1 до +1.
Если r отрицательна – это обратная зависимость между х и у, т.е. с увеличением х уменьшается у и наоборот.
Если r =0 – связь между х и у отсутствует.
Если 0 < r < 1 – связь функциональная.
Следовательно в рассмотренном примере связь между валовой продукцией и основными производственными фондами функциональная.
Коэффициент эластичности. В экономическом анализе часто используют рассчитываемые на основе уравнений регрессии коэффициенты эластичности результативного признака относительно факторного.
Коэффициент эластичности (Э) показывает, на сколько процентов изменяется в среднем результативный признак (y) при изменении факторного признака (х) на 1%.
Коэффициент эластичности для большинства форм связи величина переменная, т.е. изменяется с изменением фактора (х).
Так, для линейной зависимости (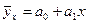 ) коэффициент эластичности рассчитывается по формуле
) коэффициент эластичности рассчитывается по формуле
Э=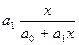
| (10.8) |
Непараметрические методы оценки корреляционной связи показателей. При исследовании степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, возможно использование следующих расчетных таблиц.
| a | b | a+b |
| c | d | c+d |
| a+c | b+d | a+b+c+d |
Теснота связи между качественными показателями рассчитывается по следующим коэффициентам:
а) коэффициент ассоциации Д.Юла
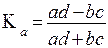
| (10.9) |
Связь имеется если коэффициент больше или равен 0,5.
б) коэффициент контингенции К.Пирсона
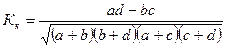
| (10.10) |
Связь имеется если коэффициент больше или равен 0,3.
 2014-02-18
2014-02-18 369
369








