Таким образом, если разбить плоское движение тела на поступательное со

Просуммировав по всем материальным точкам, получим

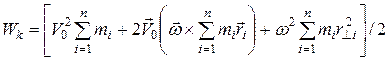
или 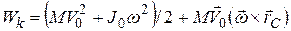, (12)

где М – полная масса тела, 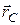– радиус-вектор центра масс, 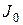- момент инерции тела относительно оси, проходящей через точку О.

Если в качестве точки О взять центр масс тела С, то 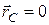и формула (12) упрощается: 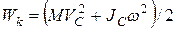. (13)

скоростью центра масс V _c и вращательное с угловой скоростью w вокруг оси, проходящей через центр масс тела, то кинетическая энергия распадается на два независимых слагаемых, одно из которых определяется только скоростью центра масс V _c, а другое – угловой скоростью w.

Из (13) следует, что при вращении тела относительно оси z, проходящей через центр масс С, его кинетическая энергия 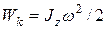. (14)