Обмен через дисперсионную среду

Рассмотрим основные кинетические закономерности межмицеллярного обмена солюбилизированными молекулами, происходящего через дисперсионную среду. Возмем для примера водный мицеллярный раствор, в котором кроме молекул ПАВ, образующих мицеллы, находятся гидрофобные молекулы Q, солюбилизированные в этих мицеллах.

Пусть М - полное число мицелл, Q - полное число молекул в единице объема мицеллярного раствора. Обозначим через М_n число мицелл, содержащих n солюбилизированных молекул, и соответственно

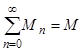(5)

Молекулы могут находиться не только в мицеллах, но и частично растворяться в водной среде. Поэтому полная их концентрация будет равна

Q = Q_s + m M (6)

где Q_s - значение растворимости молекул в воде. Как правило, Q_s << Q.

Величина m = (Q-Q_s)/M - есть среднее число солюбилизированных молекул на одну мицеллу. Чаще всего, m» 1 и в редких случаях может превышать значение 10¹. Это означает, что величины Dm» m» 1. Можно ввести функцию распределения молекул по мицеллам P_n = M_n/M, которая удовлетворяет условию нормировки

(7)

и ее первый момент есть среднее число солюбилизированных молекул на мицеллу:

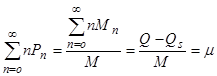(8)

Конкретный вид функции распределения P_n определяется характером межмолекулярного взаимодействия данной системы и способом приготовления системы. Простейший случай независимого случайного распределения молекул приводит к распределению Пуассона

P_n = 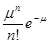(9)

которое можно получить на основе рассмотрения динамического равновесия молекул Q между мицеллярной фазой и водной средой. Предположим, что вероятность в единицу времени входа молекулы из раствора в данную мицеллу M_n не зависит от n, т.е. от того, сколько молекул находится в мицелле, и равна k ₊ Q_s, а вероятность выхода молекулы из мицеллы M_n равна k_n, где k ₊ - константа скорости второго порядка процесса Q_s + M, а k _ - вероятность в единицу времени выхода из мицеллы отдельно взятой молекулы. Тогда динамика процессов обмена молекул определяется следующей схемой

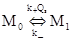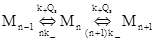, ……. ,… (10)

следуя которой, можно записать бесконечную систему кинетических уравнений:

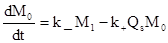
………………………….. (11)

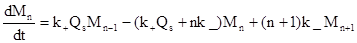
В условии динамического равновесия (производные по времени равны нулю) получается следующая система алгебраических уравнений, решение которой легко получить

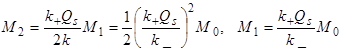
………………………………………………………. (12)

M_n =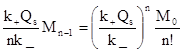

Суммируя уравнения (12), получим

M = 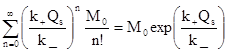(13)

и, следовательно, искомая равновесная функция распределения

P_n=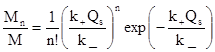 (14)

является функцией распределения Пуассона, где среднее число молекул на мицеллу m = k₊Q_s / k _.

Общее решение бесконечной системы уравнений, дающее временную зависимость P_n(t), можно получить методом производящей функции, который уже был рассмотрен в лекции 3. Напомним, что производящая функция (или более правильно ее называют производящей функцией факториальных моментов функции распределения), определяется следующей формулой:

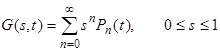(15)

Основное свойство производящей функции состоит в том, что функция распределения P_n находится простым n-кратным дифференцированием в соответствии со следующей формулой:

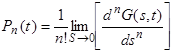(16)

Разделив почленно уравнение (6) на k_M, получим

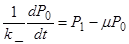
……………………………………………………. (17)

Умножив каждое из уравнений (12) почленно на sⁿ и просуммировав все уравнения, получим дифференциальное уравнение для производящей функции

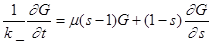(18)

Стационарное решение уравнения (13) находится элементарно. Приравнивая правую часть (13) к нулю и принимая во внимание, что

G (1,¥) = 1

получаем

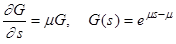(19)

Отсюда стационарная функция распределения

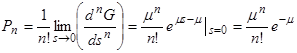(20)

Общее решение уравнения (13) имеет вид:

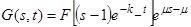(21)

где F(y) - произвольная функция, такая что F (0) = 1. Конкретное решение временной задачи будет зависеть от начального условия, то есть конкретного вида начальной функции распределения.

В качестве примера рассмотрим эволюцию функции распределения системы, получаемой мгновенным смешением двух мицеллярных растворов, содержащих одинаковое число мицелл, при этом один из них не содержит солюбилизированных молекул, а в другом среднее число солюбилизированных молекул равно 2 m, и их распределение определяется функцией распределения Пуассона. Таким образом, общая начальная функция распределения всей рассматриваемой системы имеет вид:

P_n(0) = 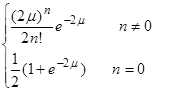(22)

Из формул (15) и (21) при t = 0 следует уравнение:

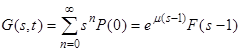(23)

Вид функции F(y) можно найти из начального условия (22), т.е. подставив в (23) выражение (22) и сделав соответствующие преобразования, получим

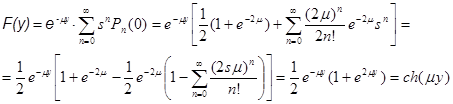(24)

Следовательно

G(s,t) = e^-m(s-1) ch [ m(s-1) e^-k_t ] (25)

и подставляя (19) в (11), после преобразований получаем:

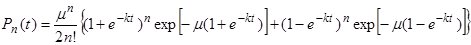(26)

Таким образом, функция распределения (20) представляет собой сумму двух пуассоновских распределений. Одно отражает временную эволюцию той части мицеллярного раствора, в которой до смешения находились солюбилизированные молекулы, и среднее число молекул в нем со временем уменьшается по экспоненциальному закону, стремясь в пределе при t®¥ к значению m.

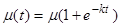(27)

и аналогично другое распределение отвечает за временную эволюцию второй части мицеллярного раствора, в котором до смешения не было солюбилизированных молекул, и среднее число молекул в этих мицеллах увеличивается в соответствии с формулой

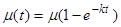. (28)