Найдем 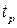 для случаев разных законов распределения.
для случаев разных законов распределения.
1. Нормальное распределение. Его плотность, как известно, равна:
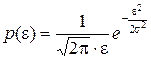 (17)
(17)
Подставим (17) в (15), получим:
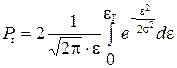 (18)
(18)
После замены: 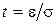 ;
; 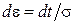 ;
; 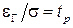 , (18) примет вид:
, (18) примет вид:
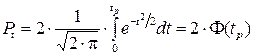 (19)
(19)
Функция 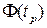 называется интегралом вероятностей. Его значения приводятся в виде таблицы в математических справочниках. На основе этих данных составлена следующая таблица:
называется интегралом вероятностей. Его значения приводятся в виде таблицы в математических справочниках. На основе этих данных составлена следующая таблица:
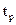
| 2/3 | 0,95 | 0,997 | |
| Pt | 0,5 | 0,68 |
Из этой таблицы следует, что при нормальном распределении доверительная вероятность нахождения случайной погрешности в интервале от 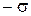 до
до 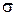 (
(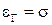 ) равна всего 0,68. В то же время
) равна всего 0,68. В то же время
при 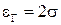 , Pt = 0,95,
, Pt = 0,95,
при 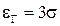 , Pt = 0,997. (20)
, Pt = 0,997. (20)
Кстати Чебышевым доказано, что при 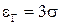 , Pt > 0,9 при любых законах распределения. Данное неравенство называется неравенством Чебышева.
, Pt > 0,9 при любых законах распределения. Данное неравенство называется неравенством Чебышева.
2. 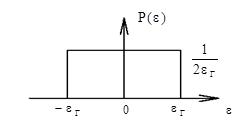 Равномерный закон распределения, как известно, имеет вид рис. 3:
Равномерный закон распределения, как известно, имеет вид рис. 3:
Подставив его 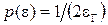 в (13), получим
в (13), получим
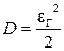 , т. е.
, т. е. 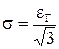
 Как видим, в этом случае доверительная вероятность равна
Как видим, в этом случае доверительная вероятность равна 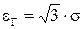 при
при 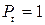 . (21)
. (21)
3.  Треугольный закон распределения (рис. 4). Аналогичным способом
Треугольный закон распределения (рис. 4). Аналогичным способом 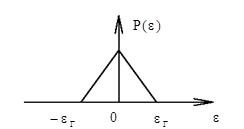 можно найти, что для него
можно найти, что для него 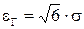 при
при 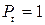 .
.
 2014-02-18
2014-02-18 429
429







