Как известно результат измерения равен сумме:
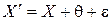 (8)
(8)
Случайная погрешность на практике обычно существенно превышает систематическую. При многократном измерении средний результат измерении 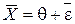 , среднее граничное значение
, среднее граничное значение 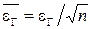 , выбирая число измерений
, выбирая число измерений 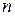 , можно добиться, чтобы
, можно добиться, чтобы 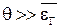 , тогда результат измерения
, тогда результат измерения
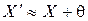 (9)
(9)
Отсюда систематическая погрешность
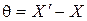 (10)
(10)
Для исключения систематической погрешности нужно вычесть 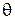 из полученного результата измерения
из полученного результата измерения
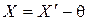 (11)
(11)
Это можно произвести введением поправки к результату измерения 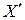 равной
равной 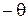 , тогда поправку прибавляют к
, тогда поправку прибавляют к 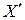
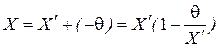 (12)
(12)
 В (12) последний множитель
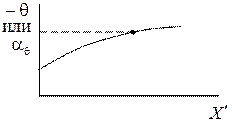
В (12) последний множитель 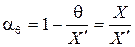 называется поправочным коэффициентом. Поправочный коэффициент или поправка может быть представлена в виде графика (рис. 2), либо в виде таблицы.
называется поправочным коэффициентом. Поправочный коэффициент или поправка может быть представлена в виде графика (рис. 2), либо в виде таблицы.
Выявление и исключение 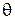 может выполняться теоретически или экспериментально; до, в процессе или после измерения, автоматически или вручную. Однако, теоретическое определение
может выполняться теоретически или экспериментально; до, в процессе или после измерения, автоматически или вручную. Однако, теоретическое определение 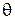 возможно редко.
возможно редко.
Рассмотрим следующий пример (рис.3):
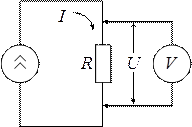
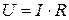
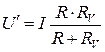 , где
, где 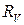 — это сопротивление вольтметра, которое вводит в измерение
— это сопротивление вольтметра, которое вводит в измерение 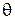
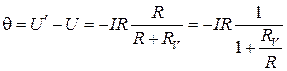
Так как нам не известен ток 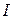 , то в данном случае необходимо использовать поправочный коэффициент, он равен:
, то в данном случае необходимо использовать поправочный коэффициент, он равен:
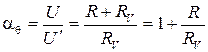 ,
,
отсюда следует, что при измерении нужно стремиться, чтобы 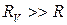 .
.
 2014-02-18
2014-02-18 317
317







