2014-02-18
1334
Допустим, что в каждом эксперименте проверяется, какое произошло событие из некоторого разбиения пространства элементарных исходов W -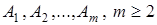 
. Когда число m равнялось двум, то в качестве полной группы брались события 
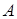и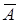 
- “успех” и “неудача”. Если всего проводится n независимых экспериментов, то элементарный исход можно описать перестановкой с повторениями из чисел 1, 2,…, m; в перестановке n элементов, число l (1£ l £ m) на i- м месте (1£ i £ n) означает, что в i- м эксперименте произошло событие 
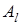. Если в n независимых испытаниях событие 
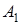произошло 
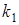раз, событие 
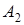произошло 
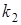раз, …, событие 
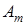произошло 
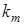раз,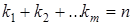 
, то вероятность всякого такого элементарного исхода равна по определению произведению 
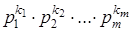. Здесь 
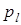- вероятность события 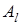, причем 
.
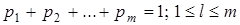Всего же подобных элементарных исходов столько, сколько перестановок с повторениями, т.е.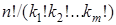 
.
Следовательно, вероятность того, что в n независимых испытаниях Событие 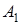появится 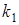раз, 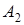появится 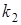раз, …, событие 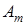появится 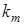раз, 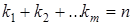, равна:
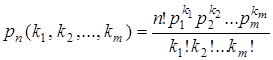. (6.4)
