В гидродинамике жидкость или газ рассматривается как сплошная среда. Это значит, что всякий малый элемент объема жидкости считается все-таки настолько большим, что содержит еще очень большое число молекул. Поэтому, когда мы будем говорить о бесконечно малых элементах объема, то всегда при этом будет подразумеваться объем достаточно малый по сравнению с объемом тела, но большой по сравнению с молекулярными расстояниями. В таком же смысле надо понимать в гидродинамике выражения «жидкая частица», «точка жидкости». Если, например, говорят о смещении некоторой частицы жидкости, то при этом речь идет не о смещении отдельной молекулы, а о смещении целого элемента объема, содержащего много молекул, но рассматриваемого в гидродинамике как точка.
Пусть жидкость движется со скоростью v (х, у, z, t), проекции которой на оси координат обозначим v х(х, у, z, t), v y (х, у, z, t), v z(х, у, z, t).
Подчеркнем, что v (х, у, z, t) есть скорость жидкости в каждой данной точке (х, у, z, t) пространства в момент времени t, т. е. относится к определенным точкам пространства, а не к определенным частицам жидкости, передвигающимся со временем в пространстве; то же самое относится к термодинамическим величинам р(х, у, z, t), ρ(х, у, z, t).
Если поле вектора скорости v (х, у, z, t) известно, то траектории отдельных частиц жидкости будут определяться, уравнениями

Отсюда легко можно найти ускорение частицы жидкости:
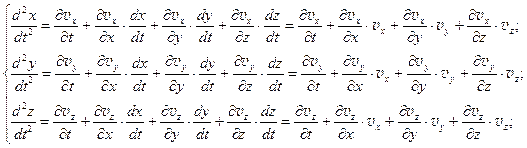 (12.15)
(12.15)
В каждый момент времени и в каждой точке жидкость находится в некотором состоянии термодинамического равновесия, определяемого давлением р(х, у, z, t), плотностью ρ(х, у, z, t), температурой Т(х, у, z, t), энтропией s(х, у, z, t) и внутренней энергией Е(х, у, z, t). Из термодинамики известно, что для каждой данной среды независимы только два из параметров р, ρ, T, s и Е. Величины р, Т и Е можно рассматривать как функции от ρ и s.
Начнем вывод основных гидродинамических уравнений с вывода уравнения, выражающего собой закон сохранения вещества в гидродинамике. Рассмотрим некоторый объем жидкости V, ограниченный поверхностью S. Если внутри объема V нет источников и стоков, то изменение в единицу времени массы жидкости, заключенной внутри V, равно потоку жидкости через поверхность S:

где vп — проекция v (х, у, z, t) на внешнюю нормаль к поверхности S. Преобразуя правую часть по формуле Остроградского и дифференцируя по t под знаком интеграла в левой части, получим:
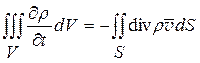 ,
,
или
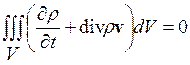 ,
,
где
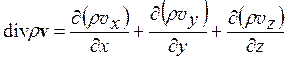
Так как последнее равенство справедливо для любого объема внутри жидкости, то отсюда следует, что
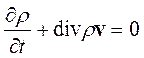 . (12.16)
. (12.16)
Это уравнение называется уравнением неразрывности.
Перейдем теперь к выводу уравнений движения идеальной жидкости.
Под идеальной жидкостью будем понимать такую сплошную среду, в которой внутренние силы — находится ли среда в состоянии равновесия или движения — приводятся к давлению, так что если выделить в этой жидкости некоторый объем V, ограниченный поверхностью S, то действие на него остальной части жидкости приводится к силе, направленной в каждой точке поверхности S по внутренней нормали. Обозначим величину этой силы, отнесенную на единицу площади (давление), через р(х, у, z, t).
Таким образом, равнодействующая сил давления, приложенных к поверхности S, равна
 ,
,
где n —единичный вектор внешней нормали к поверхности S. На основании формулы Остроградского имеем
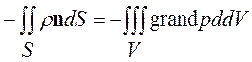
Пусть далее на жидкость действует внешняя сила F (Fх, Fy, Fz) рассчитанная на единицу массы, так что равнодействующая этих сил, приложенных к объему V, равна

Наконец, равнодействующая сил инерции, действующих на жидкость в объеме V, будет
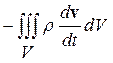 ,
,
где 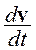 — вектор ускорения частицы жидкости. Здесь производная
— вектор ускорения частицы жидкости. Здесь производная 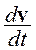 определяет не изменение скорости жидкости в данной неподвижной точке пространства, а изменение скорости определенной передвигающейся в пространстве частицы жидкости. Это подчеркивается обозначением
определяет не изменение скорости жидкости в данной неподвижной точке пространства, а изменение скорости определенной передвигающейся в пространстве частицы жидкости. Это подчеркивается обозначением 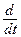 вместо
вместо 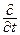 .
.
Применяя принцип Даламбера, получим
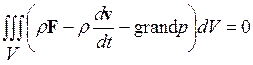
Отсюда в силу произвольности объема V следует, что
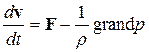 (12.17)
(12.17)
или в скалярной форме
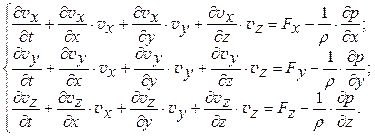 (12.18)
(12.18)
Это есть уравнения движения идеальной жидкости в форме Эйлера. Итак, для пяти неизвестных функций vx, vу, v z, ρ и р мы имеем всего четыре уравнения (12.16) и (12.18). Чтобы получить еще одно уравнение, будем считать, что движение жидкости происходит адиабатически. При адиабатическом движении энтропия каждой частицы жидкости остается постоянной (хотя может меняться от частицы к частице при перемещении последней в пространстве, т. е. 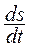 = 0, где полная производная по времени означает, как и в (12.17), изменение энтропии определенной передвигающейся в пространстве частицы жидкости. Эту производную можно записать в виде
= 0, где полная производная по времени означает, как и в (12.17), изменение энтропии определенной передвигающейся в пространстве частицы жидкости. Эту производную можно записать в виде
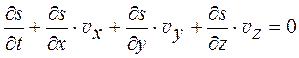
Это есть уравнение, выражающее собой адиабатичность движения идеальной жидкости. В частном случае может оказаться, что и некоторый начальный момент времени энтропия одинакова во всех точках жидкости, тогда она останется везде одинаковой и неизменной со временем и при дальнейшем движении жидкости. В этом случае уравнение адиабатичности можно писать просто в виде
s = s 0 = const.
Такое движение жидкости называют изэнтропческим. При этом
p = f (ρ, s 0) = f (ρ) (12.19)
Таким образом, мы имеем пять уравнений: уравнение неразрывности (12.16), три уравнения движения идеальной жидкости (12.18) и уравнение (12.19). Эти уравнения содержат как раз пять неизвестных функций: vx, vу, v z, ρ и р.
2. Колебательное движение с малыми амплитудами в сжимаемой жидкости или газе называют звуковыми волнами. В каждом месте жидкости в звуковой волне происходят попеременные сжатия и разрежения.
В силу малости колебаний в звуковой волне скорость v в ней мала, так что в уравнениях Эйлера (12.18) можно пренебречь членами 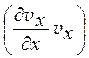 и т.д. По той же причине относительные изменения плотности и давления в жидкости тоже малы. Положим
и т.д. По той же причине относительные изменения плотности и давления в жидкости тоже малы. Положим
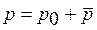 ,
, 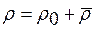 , (12.20)
, (12.20)
где р 0, ρ 0— постоянные равновесные плотность и давление жид кости, а р и ρ — их изменения в звуковой волне (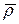 << ρ 0,
<< ρ 0, 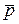 << р — называют звуковым давлением.
<< р — называют звуковым давлением.
Уравнение непрерывности (12.16) при подстановке в него (12.20) и пренебрежении малыми величинами второго порядка (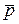 ,
,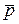 , v,
, v, 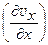 ,
,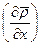 ,
, 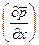 ,и т. д. надо при этом считать малыми величинами первого порядка) примет вид
,и т. д. надо при этом считать малыми величинами первого порядка) примет вид
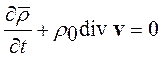
или, полагая
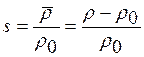
получим
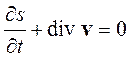 . (12.21)
. (12.21)
Уравнения Эйлера (12.18), считая, что внешние силы отсутствуют, в том же приближении сводятся к уравнениям
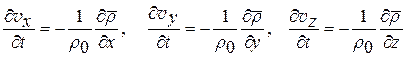
или, в векторной форме,
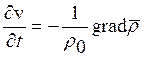 . (12.22)
. (12.22)
Уравнения (12.21) и (12.22) содержат неизвестные функции 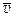 , s и
, s и 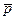 . Для исключения одной из них обратимся к уравнению: p = f (ρ, s 0) = f (ρ), которое в том же приближении можно записать в виде
. Для исключения одной из них обратимся к уравнению: p = f (ρ, s 0) = f (ρ), которое в том же приближении можно записать в виде
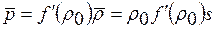 . (12.23)
. (12.23)
Подставляя (12.23) в уравнение (12.22), получим
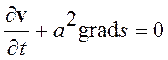 , (12.24)
, (12.24)
где положено а 2 = 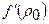 , так как для всех жидкостей и газов, встречающихся в природе, при постоянной энтропии, давление возрастает при возрастании плотности, т. е.
, так как для всех жидкостей и газов, встречающихся в природе, при постоянной энтропии, давление возрастает при возрастании плотности, т. е. 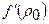 >0.
>0.
Применяя к уравнению (12.24) операцию дивергенции и переставши дифференцирование по I с операцией дивергенции, будем иметь
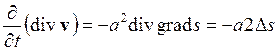 , (12.25)
, (12.25)
где 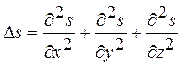
Принимая во внимание уравнение (12.25), получим
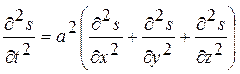 (12.26)
(12.26)
Для давления 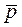 и скорости v также можно получить волновое уравнение вида (12.26).
и скорости v также можно получить волновое уравнение вида (12.26).
Предположим теперь, что в начальный момент существует потенциал скоростей и 0 (х, у, z), т. е.
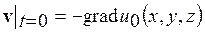 (12.27)
(12.27)
Из уравнения (12.24) следует, что
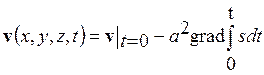
или, в силу (12.27),
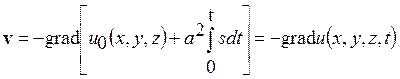 (12.28)
(12.28)
которое означает, что существует потенциал скоростей и(х, у, z, t) в любой момент времени t:
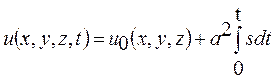 . (12.29)
. (12.29)
Покажем, что потенциал скоростей и(х, у, z, t) удовлетворяет волновому уравнению. В самом деле, дифференцируя выражение (12.29) два раза по t, получим
 (12.30)
(12.30)
С другой стороны,
 . (12.31)
. (12.31)
Сравнивая (12.30) и (17), получим
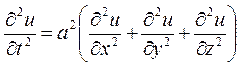 (12.32)
(12.32)
Отметим, что знание потенциала скоростей и(х, у, z, t) достаточно для определения всего процесса движения жидкости или газа, так как
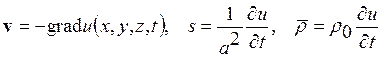 .
.
 2014-02-18
2014-02-18 1098
1098