Пример
Доказательство
§ НОД(0, r) = r для любого ненулевого r (т.к. 0 делится на любое целое число, кроме нуля).
Проще сформулировать алгоритм Евклида так: если даны натуральные числа a и b и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.
Для иллюстрации, алгоритм Евклида будет использован, чтобы найти НОД a = 1071 и b = 462. Для начала, от 1071 отнимем кратное значение 462, пока не получим знаменатель меньше чем 462. Мы должны дважды отнять 462, (q 0 = 2), оставаясь с остатком 147
1071 = 2 × 462 + 147.
Затем от 462 отнимем кратное значение 147, пока не получим знаменатель меньше чем 147. Мы должны трижды отнять 147 (q 1 = 3), оставаясь с остатком 21.
462 = 3 × 147 + 21.
Затем от 147 отнимем кратное значение 21, пока не получим знаменатель меньше чем 21. Мы должны семь раз отнять 21 (q 2 = 7), оставаясь без остатка.
147 = 7 × 21 + 0.
Таким образом последовательность a>b>R1>R2>R3>R4>...>Rn в данном конкретном случае будет выглядеть так:
1071>462>147>21
Так как последний остаток равен нулю, алгоритм заканчивается числом 21 и НОД(1071, 462)=21.
В табличной форме, шаги были следующие
| Шаг k | Равенство | Частное и остаток |
| 1071 = q 0 462 + r 0 | q 0 = 2 и r 0 = 147 | |
| 462 = q 1 147 + r 1 | q 1 = 3 и r 1 = 21 | |
| 147 = q 2 21 + r 2 | q 2 = 7 и r 2 = 0; алгоритм заканчивается |
Расширенный алгоритм Евклида
a = bq 0 + r 1
Основная статья: Соотношение Безу
Формулы для ri могут быть переписаны следующим образом:
r 1 = a + b (− q 0)
r 2 = b − r 1 q 1 = a (− q 1) + b (1 + q 1 q 0)
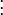
НОД (a, b) = rn = as + bt
здесь s и t целые. Это представление наибольшего общего делителя называется соотношением Безу, а числа s и t — коэффициентами Безу. Соотношение Безу является ключевым в доказательстве леммы Евклида и основной теоремы арифметики.
 2014-02-18
2014-02-18 8381
8381
