Свойства. Число a делится нацело на b тогда и только тогда, когда остаток от деления a на b равен нулю

Число a делится нацело на b тогда и только тогда, когда остаток от деления a на b равен нулю.

§ Всякое число, делящее как a, так и b, называется их общим делителем; максимальное из таких чисел называется наибольшим общим делителем. У всякой пары целых чисел есть по крайней мере два общих делителя: +1 и -1. Если других общих делителей нет, то эти числа называются взаимно простыми.

§ Два целых числа a и b называются равноделимыми на целое число m, если либо и a, и b делится на m, либо ни a, ни b не делится на него.

Замечание: во всех формулах этого раздела предполагается, что 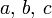— целые числа.

§ Любое целое число является делителем нуля, и частное равно нулю:

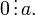
§ Любое целое число делится на единицу:

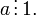
§ На ноль делится только ноль:

,

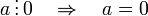причём частное в этом случае не определено.

§ Единица делится только на единицу:

§ Для любого целого числа 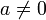найдётся такое целое число 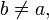для которого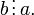

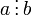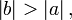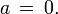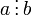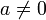§ Если и то Отсюда же следует, что если и то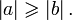

§ Для того чтобы 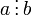необходимо и достаточно, чтобы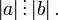

§ Если 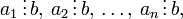то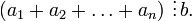

§ Свойство делимости является отношением нестрогого порядка и, в частности, оно:

§ рефлексивно, т.е. любое целое число делится на себя же: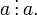

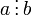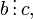§ транзитивно, т.е. если и то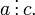

§ антисимметрично, т.е. есл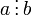и и 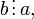то л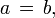ибо либо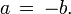

Теорема Эйлера

Теоре́ма Э́йлера в теории чисел гласит: Если a и m взаимно просты, то 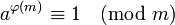, где φ(m) — функция Эйлера