Основна́я теоре́ма арифме́тики утверждает:
Каждое натуральное число n > 1 представляется в виде 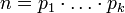 , где
, где 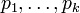 — простые числа, причём такое представление единственно с точностью до порядка следования сомножителей
— простые числа, причём такое представление единственно с точностью до порядка следования сомножителей
Единицу можно также считать произведением нулевого количества простых чисел, «пустым произведением».
Как следствие, каждое натуральное число n единственным образом представимо в виде
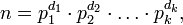 где
где 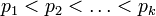 — простые числа, и
— простые числа, и 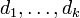 — некоторые натуральные числа.
— некоторые натуральные числа.
Такое представление числа n называется его каноническим разложением на простые сомножители.
Если простое число p делит без остатка произведение двух целых чисел 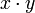 , то p делит x или y например 5*6=30,допустим р=3, если 30/3=10- без остатка, то 6 тоже делится на 3 или
, то p делит x или y например 5*6=30,допустим р=3, если 30/3=10- без остатка, то 6 тоже делится на 3 или
Коммутативность сложения. 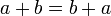
1. Коммутативность умножения. 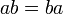
2. Ассоциативность сложения. 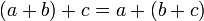
3. Ассоциативность умножения. 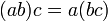
4. Дистрибутивность умножения относительно сложения. 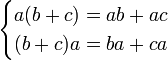
 2014-02-18
2014-02-18 578
578








