Задание для самостоятельной работы.
ГЛАВА 4. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ
ГЛАВА 3. ВРЕМЕННЫЕ РЯДЫ. ГЕТЕРОСКЕДАСТИЧНОСТЬ И АВТОКОРРЕЛИРОВАННОСТЬ
.
Вероятности оптических переходов. Дипольно- разрешенные переходы. Переходы, запрещенные по симметрии. Приближение Герцберга –Теллера. Поглощение фотонов, излучение фотонов. Спин-орбитальное взаимодействие и вероятности запрещенных по мультиплетности переходов
Оператор взаимодействия молекулярной системы с электромагнитным полем имеет вид:
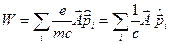 атомные единицы
атомные единицы
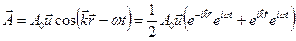
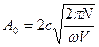
векторный потенциал 
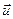 -вектор поляризации света (направление электрического вектора)
-вектор поляризации света (направление электрического вектора)
Дипольное приближение: 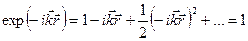
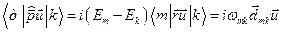 с точностью до заряда дипольный момент перехода. Синглет-синглетный
с точностью до заряда дипольный момент перехода. Синглет-синглетный 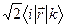
Сила осциллятора перехода:
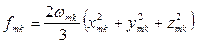
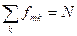
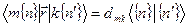 Приближение Кондона. Колебательная структура.
Приближение Кондона. Колебательная структура.
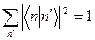
Эксперимент.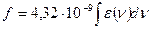 , где ε- молярный коэффициент экстинции в
, где ε- молярный коэффициент экстинции в 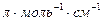 , ν - частата перехода в
, ν - частата перехода в 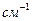 .
.
π-π* разрешены в дипольном приближении, поляризованы в плоскости молекулы, 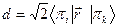 d ~ 1, f ~ 0,1-1
d ~ 1, f ~ 0,1-1
n-π* разрешены в дипольном приближении в плоских молекулах только,если n -орбиталь содержит вклад s - орбитали. Азаароматические молекулы (пиридин и др.) Гибридизация n - sp2
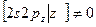 , f~ 10-2-510-2 Поляризованы перпендикулярно плоскости молекулы
, f~ 10-2-510-2 Поляризованы перпендикулярно плоскости молекулы
σ-π*, π-σ* Поляризованы перпендикулярно плоскости молекулы
Переходы, запрещенные по симметрии. n-π* в плоских карбонилсодержащих молекулах
Теория Герцберга –Теллера. Разложение по функциям грубого(!) адиабатического приближения.
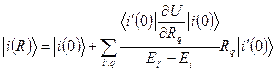
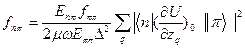
fnπ*~ 10-4 fσπ *~10-4
Переходы запрещенные по мультиплетности.
Спин-орбитальное взаимодействие.
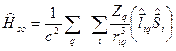
Учитывая правила действия операторов проекций спинового момента на спиновые функции
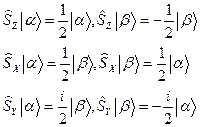
Тогда можно записать:
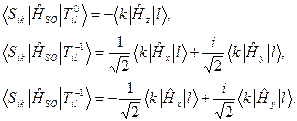
 Здесь
Здесь
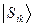 волновая функция возбужденного синглетного состояния в одно конфигурационном приближении,получающаяся из конфигурации основного состояния при переходе электрона с орбитали
волновая функция возбужденного синглетного состояния в одно конфигурационном приближении,получающаяся из конфигурации основного состояния при переходе электрона с орбитали 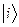 на
на 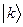 ,
, 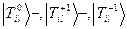 - волновые функции триплетных состояний с проекцией спинового момента на ось равными 0,+1 и –1.
- волновые функции триплетных состояний с проекцией спинового момента на ось равными 0,+1 и –1.  ,
,
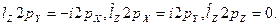

ππ*- ππ* Только трехцентровые: 0,3-1 см-1
nπ*-ππ* (ππ*-σπ*)
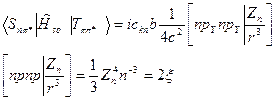
ξ -константа сверхтонкого расщепления атома.
~10-50см-1 атомы N, O, S. ~100-1000 см-1 атомы Br, J
Неплоские молекулы.
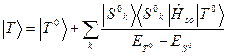
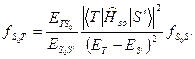

f Tnπ* (Sππ*) ~ 10-6-10-7 в плоскости молекулы
f Tππ* (Snπ* , Sπσ, S σπ*)~ 10-9-10-10 имеет внеплоскостную составляющую
Излучательные переходы
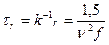 В сек, если ν измеряется в см-1.
В сек, если ν измеряется в см-1.
Синглет- синглетные (флуоресценция)
ππ* 10-8-10-9 с
nπ* 10-5-10-6 с
Триплет-синглетные (фосфоресценция)
ππ* 0,1-10 с
nπ* 10-2-10-3 с
Колебательная структура
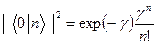
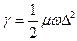
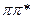 Валентные С-С (1400см-1), деформационные С-С-С (600см-1)
Валентные С-С (1400см-1), деформационные С-С-С (600см-1)
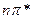 Валентные С=О деформационные C-N-C (1700см-1; 500см)
Валентные С=О деформационные C-N-C (1700см-1; 500см)
В качестве примера модели множественной линейной регрессии рассмотрим обобщение предыдущей задачи. Имеются следующие данные (условные) о сменной добыче угля на одного рабочего 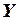 (т), мощности пласта
(т), мощности пласта 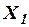 (ранее обозначалась
(ранее обозначалась 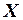 ) и уровне механизации работ
) и уровне механизации работ 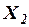 (%), характеризующие процесс добычи угля в 10 шахтах:
(%), характеризующие процесс добычи угля в 10 шахтах:
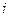
| ||||||||||
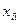
| ||||||||||
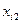
| ||||||||||
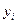
|
В предположении, что между переменными 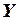 ,
, 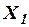 и
и 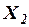 существует линейная регрессионная зависимость:
существует линейная регрессионная зависимость:
1) найти ее аналитическое выражение (уравнение регрессии 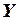 по
по 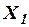 и
и 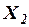 ),
),
2) найти 95%-ные доверительные интервалы для индивидуального и среднего значений сменной добычи угля на 1 рабочего для таких же шахт,
3) проверить значимость коэффициентов регрессии и построить для них 95%-ные доверительные интервалы,
4) найти интервальную оценку для дисперсии 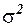 .
.
1) Модель множественной линейной регрессии можно представить в виде:
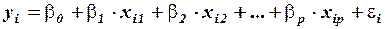 ,
,
где
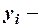
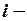 е наблюдение зависимой переменной
е наблюдение зависимой переменной 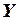 (
(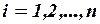 ),
),
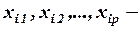 объясняющие переменные,
объясняющие переменные,
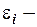
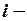 я случайная составляющая, характеризующая отклонение от функции регрессии.
я случайная составляющая, характеризующая отклонение от функции регрессии.
Введем обозначения: 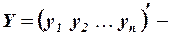 матрица-столбец, или вектор, значений зависимой переменной размера
матрица-столбец, или вектор, значений зависимой переменной размера 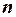 ;
; 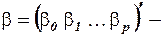 матрица-столбец, или вектор,параметров размера
матрица-столбец, или вектор,параметров размера 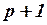 ;
; 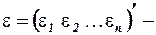 матрица-столбец, или вектор, возмущений (случайных ошибок, остатков) размера
матрица-столбец, или вектор, возмущений (случайных ошибок, остатков) размера 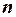 ;
;
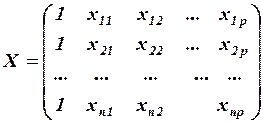
- матрица-столбец, или вектор, значений объясняющих переменных размера 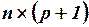 ; в матрицу
; в матрицу 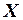 дополнительно введен столбец, все элементы которого равны 1, т.е. предполагается, что свободный член
дополнительно введен столбец, все элементы которого равны 1, т.е. предполагается, что свободный член 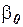 умножается на фиктивную переменную
умножается на фиктивную переменную 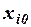 , принимающую значение 1 для всех
, принимающую значение 1 для всех 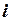 :
: 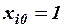
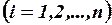 .
.
Тогда в матричной форме модель множественной линейной регрессии примет вид:
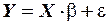 .
.
Оценкой этой модели по выборке является уравнение
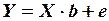 ,
,
где 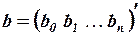 ,
, 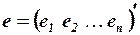 .
.
Для оценки вектора неизвестных параметров 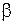 применим метод наименьших квадратов, согласно которому вектор неизвестных параметров
применим метод наименьших квадратов, согласно которому вектор неизвестных параметров 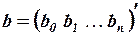 выбирается таким образом, чтобы сумма квадратов отклонений эмпирических значений
выбирается таким образом, чтобы сумма квадратов отклонений эмпирических значений 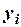 от значений
от значений 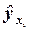 , найденных по уравнению регрессии, была минимальной:
, найденных по уравнению регрессии, была минимальной:

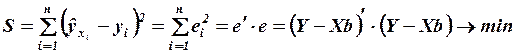 ,
,
при этом используется свойство произведения 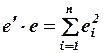 . С учетом свойства транспонирования произведения матриц
. С учетом свойства транспонирования произведения матриц 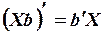 после раскрытия скобок условие минимизации примет вид:
после раскрытия скобок условие минимизации примет вид:
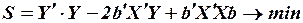 .
.
Можно доказать, что задача минимизации функции 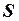 сводится к определению вектора
сводится к определению вектора 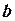 неизвестных параметровиз следующего матричного уравнения:
неизвестных параметровиз следующего матричного уравнения:
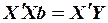 ,
,
при этом матрица 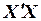 сумм первых степеней, квадратов и попарных произведений
сумм первых степеней, квадратов и попарных произведений 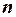 наблюдений и вектор
наблюдений и вектор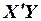 произведений
произведений 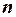 наблюдений объясняющих и зависимой переменных имеют вид:
наблюдений объясняющих и зависимой переменных имеют вид:
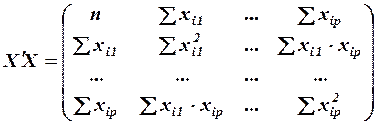 ,
, 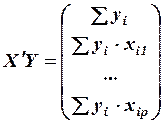 .
.
Решением матричного уравнения 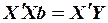 является вектор
является вектор
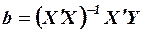 ,
,
где 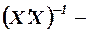 матрица, обратная матрице коэффициентов
матрица, обратная матрице коэффициентов 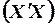 ,
, 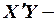 матрица-столбец, или вектор, ее свободных членов.
матрица-столбец, или вектор, ее свободных членов.
Зная вектор 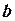 , выборочное уравнение множественной регрессии можно представить в виде:
, выборочное уравнение множественной регрессии можно представить в виде:
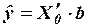 ,
,
где 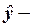 групповая (условная) средняя переменной
групповая (условная) средняя переменной 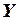 при заданном векторе значений объясняющей переменной
при заданном векторе значений объясняющей переменной 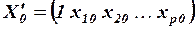 .
.
Для заданного примера
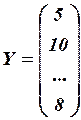 ,
, 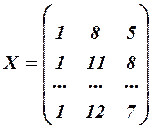 .
.
Для удобства вычислений составляем вспомогательную таблицу.
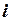
| 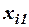
| 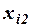
| 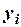
| 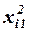
| 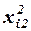
| 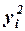
| 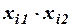
| 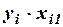
| 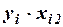
| 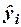
| 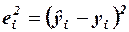
|
| 5,13 | 0,016 | ||||||||||
| 8,79 | 1,464 | ||||||||||
| 9,64 | 0,130 | ||||||||||
| 5,98 | 1,038 | ||||||||||
| 5,86 | 0,741 | ||||||||||
| 6,23 | 0,052 | ||||||||||
| 6,35 | 0,121 | ||||||||||
| 5,61 | 0,377 | ||||||||||
| 5,13 | 0,762 | ||||||||||
| 9,28 | 1,631 | ||||||||||
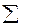
| − | 4,701 |
Вычислим матрицу 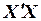 сумм первых степеней, квадратов и попарных произведений
сумм первых степеней, квадратов и попарных произведений 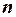 наблюдений и вектор
наблюдений и вектор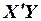 произведений
произведений 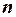 наблюдений объясняющих и зависимой переменных:
наблюдений объясняющих и зависимой переменных:
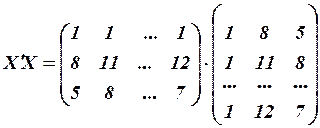 ,
, 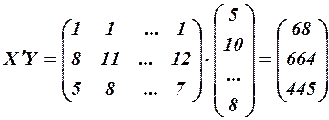 .
.
Матрицу 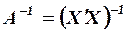 определим по формуле
определим по формуле 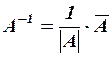 , где
, где 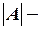 определитель матрицы
определитель матрицы 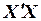 ;
; 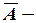 матрица, присоединенная к матрице
матрица, присоединенная к матрице 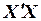 . В результате получим:
. В результате получим:
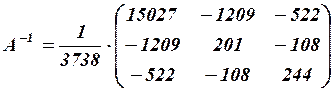 .
.
Умножая эту матрицу на вектор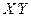 , получим:
, получим:
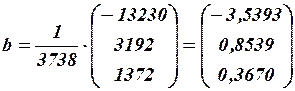 .
.
С учетом равенства 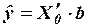 уравнение множественной регрессии имеет вид:
уравнение множественной регрессии имеет вид:
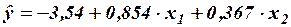 .
.
Оно показывает, что при увеличении только мощности пласта 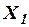 (при неизменном
(при неизменном 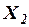 ) на 1 м добыча угля на одного рабочего
) на 1 м добыча угля на одного рабочего 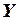 увеличивается в среднем на 0,854 т, а при увеличении только уровня механизации работ
увеличивается в среднем на 0,854 т, а при увеличении только уровня механизации работ 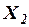 (при неизменном
(при неизменном 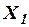 ) – в среднем на 0б367 т.
) – в среднем на 0б367 т.
Добавление в регрессионную модель объясняющей переменной 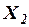 изменило коэффициент регрессии
изменило коэффициент регрессии 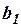 с 1,016 для парной регрессии до 0,854 – для множественной регрессии. Это объясняется тем, что во втором случае коэффициент регрессии позволяет оценить прирост зависимой переменной
с 1,016 для парной регрессии до 0,854 – для множественной регрессии. Это объясняется тем, что во втором случае коэффициент регрессии позволяет оценить прирост зависимой переменной 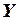 при изменении на единицу объясняющей переменной
при изменении на единицу объясняющей переменной 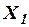 в чистом виде, независимо от
в чистом виде, независимо от 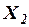 . В случае парной регрессии
. В случае парной регрессии 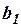 учитывает воздействие на
учитывает воздействие на 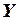 не только переменной
не только переменной 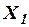 , но и косвенно корреляционно связанной с ней переменной
, но и косвенно корреляционно связанной с ней переменной 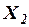 .
.
2) Формулы, используемые при построении доверительных интервалов для индивидуального и среднего значений, можно получить из аналогичных формул парной модели, изменив число степеней свободы 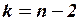 на
на 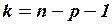 . Так, 95%-ный доверительный интервал для индивидуального значения
. Так, 95%-ный доверительный интервал для индивидуального значения 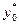 можно рассчитать по формуле:
можно рассчитать по формуле:
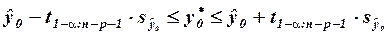 ,
,
где 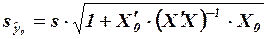 . С учетом того, что
. С учетом того, что 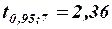 и
и 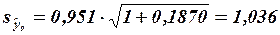 (т) окончательно получим:
(т) окончательно получим:
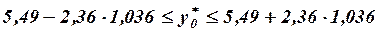 или
или 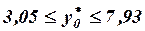 (т).
(т).
Итак, с надежностью 0,95 индивидуальная сменная добыча угля на одного рабочего в шахтах с мощностью пласта 8 м и уровнем механизации 6% находится в пределах от 3,05 до 7,93 т.
3) Проверим значимость коэффициентов регрессии 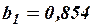 и
и 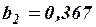 . Коэффициент
. Коэффициент 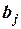 значимо отличается от нуля (иначе – гипотеза
значимо отличается от нуля (иначе – гипотеза 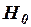 о равенстве параметра
о равенстве параметра 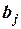 нулю, т.е.
нулю, т.е. 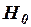 :
: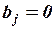 , отвергается) на уровне значимости
, отвергается) на уровне значимости 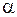 , если
, если
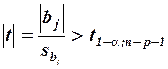 ,
,
где 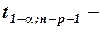 табличное значение
табличное значение 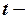 критерия Стьюдента, определенное на уровне значимости
критерия Стьюдента, определенное на уровне значимости 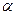 при числе степеней свободы
при числе степеней свободы 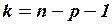 . Отсюда следует соотношение для построения доверительного интервала для параметра
. Отсюда следует соотношение для построения доверительного интервала для параметра 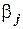 :
:
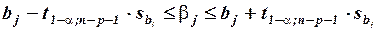 .
.
Итак, значимость коэффициентов регрессии 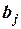 проверяется путем расчета средних квадратичных отклонений (стандартных ошибок) этих коэффициентов по формуле
проверяется путем расчета средних квадратичных отклонений (стандартных ошибок) этих коэффициентов по формуле
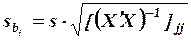
(где 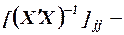 диагональный элемент матрицы
диагональный элемент матрицы 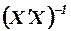 ) и использования табличного значения
) и использования табличного значения 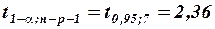 :
:
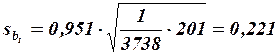 ,
, 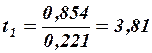 ;
;
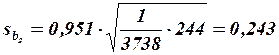 ,
, 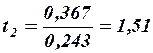 .
.
Из неравенств 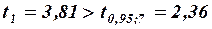 и
и 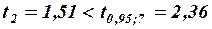 следует, что коэффициент
следует, что коэффициент 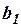 значим, а коэффициент
значим, а коэффициент 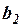 незначим.
незначим.
Доверительный интервал имеет смысл построить только для значимого коэффициента 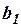 . Подстановка числовых данных в соотношение
. Подстановка числовых данных в соотношение
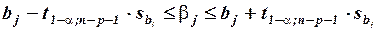
дает:
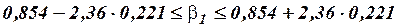 или
или 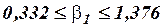 .
.
Итак, с надежностью 0,95 за счет изменения на 1 м мощности пласта 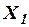 (при неизменном
(при неизменном 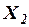 ) сменная добыча угля на одного рабочего
) сменная добыча угля на одного рабочего 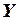 будет изменяться в пределах от 0,322 до 1,376 (т).
будет изменяться в пределах от 0,322 до 1,376 (т).
4) Найдем 95%-ный доверительный интервал для дисперсии 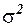 , который в множественной регрессии строится аналогично парной модели по формуле
, который в множественной регрессии строится аналогично парной модели по формуле
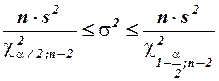
с соответствующим изменением числа степеней свободы критерия 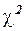 :
:
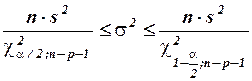 .
.
С учетом соотношения 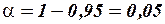 возьмем из таблицы
возьмем из таблицы 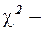 распределения
распределения 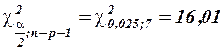 ,
, 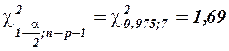 и по этой формуле найдем 95%-ный интервал для параметра
и по этой формуле найдем 95%-ный интервал для параметра 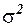 :
:
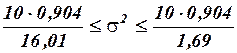 или
или 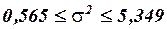 и
и 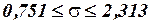 .
.
Таким образом, с надежностью 0,95 дисперсия возмущений заключена в пределах от 0,565 до 5,349, а их стандартное отклонение – от 0,751 до 2,313 (т).
2.2. Свойства оценок, полученных методом наименьших квадратов (МНК)
Зависимая переменная 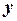 в теоретической модели регрессии
в теоретической модели регрессии
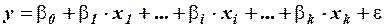
имеет две составляющие: неслучайную составляющую
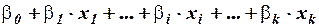
и случайную составляющую 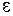 . Получаемые с помощью МНК оценки
. Получаемые с помощью МНК оценки 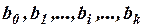 коэффициентов регрессии
коэффициентов регрессии 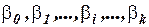 также можно представить в виде двух составляющих – неслучайной и случайной.
также можно представить в виде двух составляющих – неслучайной и случайной.
Неслучайные составляющие оценок 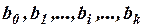 равны параметрам
равны параметрам 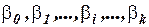 , тогда как случайные составляющие этих оценок зависят от случайной составляющей теоретической модели регрессии
, тогда как случайные составляющие этих оценок зависят от случайной составляющей теоретической модели регрессии 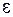 .
.
На практике разложить коэффициенты регрессии 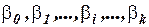 на составляющие довольно затруднительно, так как значения
на составляющие довольно затруднительно, так как значения 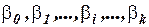 и
и 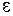 неизвестны.
неизвестны.
Регрессионный анализ, основанный на применении метода наименьших квадратов (МНК), дает наилучшие из всех возможных результаты, если выполняются следующие условия (называемые условиями Гаусса-Маркова):
1. Математическое ожидание случайного слагаемого в любом 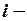 м наблюдении должно быть равно нулю –
м наблюдении должно быть равно нулю – 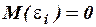 .
.
2. Дисперсия случайного слагаемого должна быть постоянной для всех наблюдений – 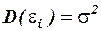 , где
, где 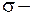 теоретическое значение среднеквадратической ошибки.
теоретическое значение среднеквадратической ошибки.
3. Случайные слагаемые должны быть статистически независимы, т.е. должно выполняться свойство некоррелированности их между собой.
4. Объясняющие переменные 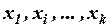 должны быть величинами неслучайными.
должны быть величинами неслучайными.
При выполнении условий Гаусса-Маркова модель
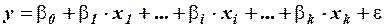
называется классической нормальной линейной регрессионной моделью. Наряду с условиями Гаусса-Маркова предполагается, что случайное слагаемое 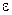 имеет нормальное распределение. При этом предположении требование некоррелированности значений случайного слагаемого эквивалентно их независимости.
имеет нормальное распределение. При этом предположении требование некоррелированности значений случайного слагаемого эквивалентно их независимости.
Первое условие означает, что нет постоянно действующего фактора, не включенного в модель, но оказывающего влияние на результативный фактор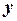 . Другими словами, случайное слагаемое не должно иметь систематического смещения. Если постоянное слагаемое включено в уравнение регрессии, то можно считать, что это условие выполняется автоматически, так как роль постоянного слагаемого как раз и заключается в том, чтобы учитывать постоянную тенденцию показателя
. Другими словами, случайное слагаемое не должно иметь систематического смещения. Если постоянное слагаемое включено в уравнение регрессии, то можно считать, что это условие выполняется автоматически, так как роль постоянного слагаемого как раз и заключается в том, чтобы учитывать постоянную тенденцию показателя 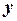 , не учтенную в уравнении регрессии.
, не учтенную в уравнении регрессии.
Если не выполнено это условие, то оценки параметров уравнения регрессии, поученное с помощью МНК, будут неэффективными и смещенными.
Второе условие означает, что дисперсия случайного слагаемого в каждом наблюдении имеет только одно значение. Другими словами, не должно быть априорной причины для того, чтобы в одних наблюдениях величина 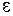 была больше, чем в других, хотя на практике величина остатков уравнения регрессии в разных наблюдениях будет разной. Но ее величина заранее неизвестна, и одна из первоочередных задач регрессионного анализа состоит в ее оценке.
была больше, чем в других, хотя на практике величина остатков уравнения регрессии в разных наблюдениях будет разной. Но ее величина заранее неизвестна, и одна из первоочередных задач регрессионного анализа состоит в ее оценке.
Если дисперсии случайного слагаемого зависят от номера наблюдения (т.е. выполняется условие гетероскедастичности), то оценки коэффициентов регрессии, полученные с помощью МНК, будут неэффективными и смещенными. Поэтому (по крайней мере, формально) можно получить более надежные оценки с использованием других методов.
Так как условия Гаусса-Маркова предполагают независимость дисперсии случайного слагаемого от номера наблюдения (т.е. предполагает выполнение условия гомоскедастичности), то разработаны специальные методы диагностирования и устранения гетероскедастичности. Характерная диаграмма рассеяния для одного из возможных вариантов гетероскедастичности показана на рис. 2.

Рис. 2. Случай гетероскедастичности остатков
Третье условие указывает, что между значениями случайного слагаемого в разных наблюдениях нет систематической связи, т.е. указывает на некоррелированность (на независимость) случайных слагаемых для разных наблюдений. Если это условие нарушается (например, для временных рядов), то имеет место автокорреляция остатков, оценки коэффициентов регрессии, полученные МНК, оказываются неэффективными. Существуют методы диагностирования и устранения автокорреляции.
Если четвертое условие (о том, что объясняющие переменные должны быть неслучайными) не выполняется, то оценки коэффициентов регрессии оказываются смещенными и несостоятельными.
Теорема Гаусса-Маркова
Если перечисленные четыре условия выполняются, то оценки, сделанные с помощью МНК, являются наилучшими оценками, так как они обладают свойствами:
1) несмещенности, что означает отсутствие систематической ошибки в положении линии регрессии;
2) эффективности – имеют наименьшую дисперсию в классе всех линейных несмещенных оценок;
3) состоятельности – при достаточно большом объеме данных оценки приближаются к истинным значениям.
Если условия Гаусса-Маркова не выполнены, то можно найти другие оценки параметров уравнения регрессии, которые будут более эффективными по сравнению с оценками, найденными методом МНК.
Кроме того, если не выполнены условия Гаусса-Маркова, то становятся неприменимы t-тесты и тест Фишера на качество оценивания и адекватность уравнения регрессии.
2.3. Анализ вариации зависимой переменной. Качество оценивания в модели множественной линейной регрессии
Пусть в уравнении регрессии содержится 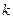 объясняющих переменных. Дисперсию зависимой переменной можно представить в виде суммы объясненной и необъясненной составляющих:
объясняющих переменных. Дисперсию зависимой переменной можно представить в виде суммы объясненной и необъясненной составляющих:
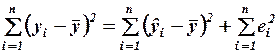 ,
,
где:
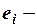 остаток в
остаток в 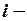 м варианте реализации событий;
м варианте реализации событий;
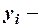 значение зависимой переменной в
значение зависимой переменной в 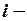 м варианте реализации событий;
м варианте реализации событий;
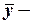 среднее значение зависимой переменной;
среднее значение зависимой переменной;
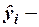 расчетное значение зависимой переменной в
расчетное значение зависимой переменной в 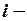 м варианте реализации событий, определяемое уравнением регрессии;
м варианте реализации событий, определяемое уравнением регрессии;
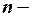 число реализации событий, в каждом из которых при сочетании значений независимых переменных было получено значение зависимой переменной.
число реализации событий, в каждом из которых при сочетании значений независимых переменных было получено значение зависимой переменной.
Каждая сумма в этом разложении имеет собственное название:
· 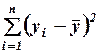 ― общий разброс зависимой переменной (обозначается
― общий разброс зависимой переменной (обозначается 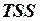 );
);
· 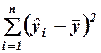 ― разброс, объясненный регрессией (обозначаетсяRSS);
― разброс, объясненный регрессией (обозначаетсяRSS);
· 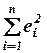 ― разброс, не объясненный регрессией (обозначаетсяESS).
― разброс, не объясненный регрессией (обозначаетсяESS).
Используя введенные обозначения, разложение дисперсии зависимой переменной можно записать в виде суммы:
TSS=RSS+ESS.
Мерой объясняющего качества уравнения регрессии по сравнению с оценкой в виде среднего значения 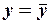 является коэффициент детерминации
является коэффициент детерминации 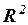 , который измеряет долю дисперсии, совместно объясненной всеми независимыми переменными:
, который измеряет долю дисперсии, совместно объясненной всеми независимыми переменными:
R2=RSS/TSS=1-ESS/TSS.
В случае коррелированности независимых переменных объясняющие способности этих переменных могут перекрываться. Для компенсации такого увеличения 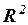 вводится приведенный (скорректированный) коэффициент детерминации с поправкой на число независимых переменных, которым можно варьировать (называемое иначе числом степеней свободы):
вводится приведенный (скорректированный) коэффициент детерминации с поправкой на число независимых переменных, которым можно варьировать (называемое иначе числом степеней свободы):
ВМЕСТО USS пишется ESS!!!!!
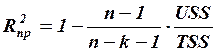 .
.
Если при добавлении новой переменной (при этом уменьшается на 1 число степеней свободы) увеличение доли объясненной регрессии мало, то скорректированный коэффициент детерминации 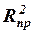 может уменьшаться, следовательно, добавлять новую переменную не следует.
может уменьшаться, следовательно, добавлять новую переменную не следует.
Качество оценок для модели множественной линейной регрессии предполагает определение статистической значимости полученных коэффициентов уравнения регрессии и коэффициента детерминации 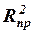 .
.
Значимость коэффициентов уравнения регрессии 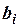 оценивается с помощью критерия
оценивается с помощью критерия 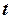 :
:
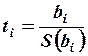 ,
,
где 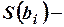 стандартные ошибки коэффициентов регрессии.
стандартные ошибки коэффициентов регрессии.
Величина 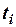 имеет распределение Стьюдента с
имеет распределение Стьюдента с 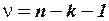 степенями свободы, где:
степенями свободы, где:
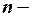 число пар данных в выборке, использованных для получения уравнения регрессии;
число пар данных в выборке, использованных для получения уравнения регрессии;
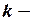 количество коэффициентов в уравнении регрессии.
количество коэффициентов в уравнении регрессии.
Алгоритм оценки значимости для коэффициентов уравнения регрессии состоит в следующем:
1) вычисляется наблюдаемое значение критерия 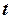 ;
;
2) по таблице распределения Стьюдента по заданному уровню значимости и числу степеней свободы 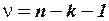 находится критическое значение
находится критическое значение 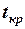 ;
;
3) вычисленные критерии 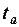 и
и 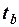 сравниваются с критическим значением
сравниваются с критическим значением 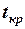 .
.
Если 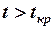 , то соответствующий коэффициент уравнения регрессии значим и принимается. Если
, то соответствующий коэффициент уравнения регрессии значим и принимается. Если 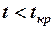 , то соответствующий коэффициент уравнения регрессии незначим, не отличается от нуля и не принимается.
, то соответствующий коэффициент уравнения регрессии незначим, не отличается от нуля и не принимается.
В эконометрике проверку гипотез осуществляют при 5%-м, реже на 10%-м уровне значимости. В первом случае стандартная ошибка оценки коэффициента регрессии составляет примерно до половины его величины. Последовательное исключение несущественных факторов (переменных), коэффициенты при которых оказались незначимы, составляют основу пошагового регрессионного анализа.
Для определения статистической значимости коэффициента детерминации 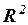 используется
используется 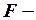 статистика:
статистика:
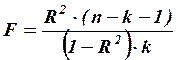 ,
,
где:
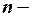 число пар данных в выборке, использованных для получения уравнения регрессии;
число пар данных в выборке, использованных для получения уравнения регрессии;
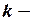 количество коэффициентов в уравнении регрессии.
количество коэффициентов в уравнении регрессии.
Величина 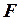 имеет распределение Фишера с
имеет распределение Фишера с 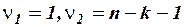 степенями свободы. Вычисленный критерий
степенями свободы. Вычисленный критерий 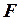 сравнивается с критической величиной
сравнивается с критической величиной 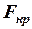 следующим образом:
следующим образом:
если 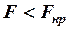 , то
, то 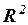 считается незначимым, он не отличим от нуля;
считается незначимым, он не отличим от нуля;
если 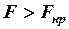 , то
, то 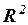 считается значимым, и уравнение регрессии может использоваться для объяснения изменения переменной
считается значимым, и уравнение регрессии может использоваться для объяснения изменения переменной 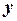 под влиянием изменения переменных
под влиянием изменения переменных 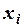 .
.
Величины критических значений критериев оценки значимости принимаются при 5%-м, реже при 10%-м уровне значимости. Указанные уровни значимости соответствуют 95%-му и 90%-му доверительным интервалам соответственно.
2.4. Дополнительные аспекты использования метода наименьших квадратов (МНК)
2.4.1. Влияние мультиколлинеарности
Мультиколлинеарность – это коррелированность двух или нескольких объясняющих переменных в уравнении множественной линейной регрессии. При наличии мультиколлинеарности оценки, формально полученные методом наименьших квадратов (МНК), обладают рядом недостатков:
1) небольшое изменение исходных данных приводит к существенному изменению оценок регрессии;
2) оценки имеют большие стандартные ошибки, малую значимость, в то время как модель в целом является значимой (при больших коэффициентах детерминации 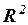 ).
).
Если при оценке уравнения регрессии несколько факторов оказались незначимыми, то нужно выяснить наличие среди них факторов, сильно коррелированных между собой. При наличии корреляции один из пары связанных между собой факторов исключается. Если статистически незначим лишь один фактор, то он должен быть исключен или заменен другим показателем. В модель регрессии включаются те факторы, которые более сильно связаны с зависимой переменной, но слабо связаны с другими факторами.
2.4.2. Спецификация переменных в уравнениях множественной линейной регрессии
Построение эконометрической модели включает в себя обоснование решения о том, какие объясняющие переменные необходимо включить в уравнение множественной линейной регрессии, т.е. как правильно составить спецификацию модели, от которой в значительной степени зависят свойства оценок коэффициентов регрессии. Здесь возможны две ситуации.
1) В модели отсутствует переменная, которая должна быть включена.
Предположим, что переменная 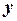 зависит от двух переменных. Однако в модель включена только одна независимая переменная
зависит от двух переменных. Однако в модель включена только одна независимая переменная 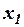 :
:
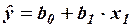 .
.
В этом случае оценка 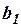 и ее дисперсия являются смещенными. Смещенность оценки связана с тем, что при отсутствии второй переменной
и ее дисперсия являются смещенными. Смещенность оценки связана с тем, что при отсутствии второй переменной 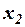 в регрессии переменная
в регрессии переменная 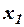 играет двойную роль: отражает свое прямое влияние и заменяет переменную
играет двойную роль: отражает свое прямое влияние и заменяет переменную 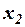 в описании ее влияния. Для данной регрессии коэффициент детерминации
в описании ее влияния. Для данной регрессии коэффициент детерминации 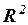 , отражающий общую объясняющую способность переменной
, отражающий общую объясняющую способность переменной 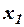 в обеих ролях, завышен.
в обеих ролях, завышен.
2) В модели включена переменная, которая не должна быть включена.
В этом случае оценки коэффициентов регрессии и их дисперсии являются несмещенными, но не эффективными. Если обнаруживается, что коэффициенты при излишних переменных статистически незначимы, то эти переменные исключаются из модели.
2.4.3. Фиктивные переменные
При исследовании влияния качественных признаков на объясняемую (зависимую) переменную 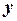 в модель множественной линейной регрессии следует вводить фиктивные переменные, принимающие, как правило, два значения: 1, если данный признак присутствует в наблюдении; 0 – при его отсутствии.
в модель множественной линейной регрессии следует вводить фиктивные переменные, принимающие, как правило, два значения: 1, если данный признак присутствует в наблюдении; 0 – при его отсутствии.
Если включаемый в рассмотрение качественный признак имеет не два, а несколько значений, то используют несколько фиктивных переменных, число которых должно быть на единицу меньше числа значений признака. При назначении фиктивных переменных исследуемая совокупность по числу значений качественного признака разбивается на группы. Одну из групп выбирают как эталонную и определяют фиктивные переменные для остальных.
Если качественный признак имеет два значения, то достаточно ввести одну фиктивную переменную. Например, строится модель, характеризующая показатели предприятий двух отраслей промышленности: электроэнергетики и газовой промышленности. Вводится фиктивная переменная, которой присваивается значение 0, если данные относятся к предприятиям электроэнергетики, и значение 1, если данные относятся к предприятиям газовой промышленности.
При трех значениях качественного признака следует вводить две фиктивные переменные. Например, строится модель, характеризующая показатели предприятий трех регионов. Вводится одна фиктивная переменная, которой присваивается значение 0, если данные относятся к предприятиям первого региона, и значение 1, если данные относятся к предприятиям двух других регионов. Второй фиктивной переменной присваивается значение 0, если данные относятся ко второму региону, и значение 1, если данные относятся к первому и третьему регионам.
Введение в регрессию фиктивных переменных существенно улучшает качество оценивания.
2.4.4. Сведение нелинейных регрессий к линейным моделям
Нелинейность регрессии может иметь место в части как переменных, так и параметров. Нелинейность по переменной можно устранить заменой переменных. Например, нелинейные уравнения
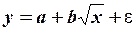 и
и 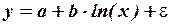
заменами переменных 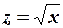 и
и 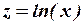 соответственно сводятся к линейным уравнениям:
соответственно сводятся к линейным уравнениям:
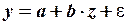 и
и 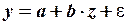 .
.
Нелинейность по параметру может устраняться различными способами. Наиболее часто нелинейность этого типа устраняется путем логарифмического преобразования уравнения. Например, нелинейные уравнения
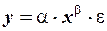 и
и 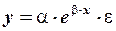
после логарифмирования сводится к линейным уравнениям относительно новых переменных и параметров 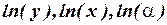 и
и 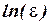 :
:
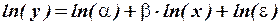 и
и 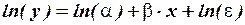 .
.
В общем случае параметры нелинейных уравнений регрессии оцениваются с использованием алгоритмов и программ, реализующих численные методы. Современные статистические пакеты программ для ПЭВМ позволяют оценивать параметры нелинейных уравнений регрессии любого типа.
2.5. Прогнозирование с помощью регрессионных уравнений
Прогнозирование – это получение оценок зависимой переменной для некоторого набора независимых переменных, отсутствующего в исходных данных. Различают точечное прогнозирование (с получением точечной оценки) и интервальное прогнозирование. В первом случае оценкой является некоторое число, во втором – интервал, в котором находится истинное значение зависимой переменной с заданным уровнем вероятности (значимости).
Точечная оценка может быть наиболее просто представлена в случае линейной модели парной регрессии:
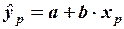 ,
,
где:
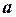 и
и 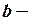 коэффициенты уравнения регрессии;
коэффициенты уравнения регрессии;
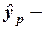 значение зависимой переменной
значение зависимой переменной 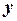 , предсказанное с использованием уравнения регрессии;
, предсказанное с использованием уравнения регрессии;
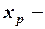 значение независимой переменной
значение независимой переменной 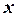 , для которого необходимо предсказать величину зависимой переменной.
, для которого необходимо предсказать величину зависимой переменной.
Ошибка предсказания представляет собой разность между предсказанным и действительным значениями. Для оценки этой ошибки определяется стандартная ошибка предсказания, которая для случая линейной регрессии определяется выражением:
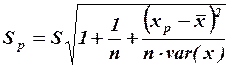 ,
,
где:
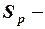 стандартная ошибка предсказания;
стандартная ошибка предсказания;
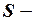 стандартная ошибка регрессии;
стандартная ошибка регрессии;
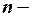 число пар данных, используемых для регрессионного анализа;
число пар данных, используемых для регрессионного анализа;
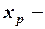 значение независимой переменной, для которого дается прогноз;
значение независимой переменной, для которого дается прогноз;
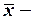 выборочное среднее переменной
выборочное среднее переменной 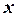 ;
;
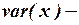 вариация переменной
вариация переменной 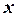 в выборке.
в выборке.
Чем больше значение 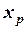 отклоняется от выборочного среднего
отклоняется от выборочного среднего 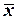 , тем больше дисперсия ошибки предсказания; чем больше объем выборки
, тем больше дисперсия ошибки предсказания; чем больше объем выборки 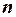 , тем меньше дисперсия этой ошибки.
, тем меньше дисперсия этой ошибки.
Доверительный интервал для прогнозируемого значения зависимой переменной 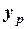 определяется по формуле:
определяется по формуле:

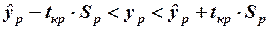 ,
,
где:
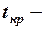 критическое значение
критическое значение 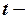 статистики Стьюдента при заданном уровне значимости и числе степеней свободы (для парной линейной регрессии
статистики Стьюдента при заданном уровне значимости и числе степеней свободы (для парной линейной регрессии 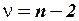 );
);
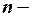 число пар данных в выборке, использованных для получения уравнения регрессии.
число пар данных в выборке, использованных для получения уравнения регрессии.
3.1. Временные ряды и их моделирование с применением фиктивных переменных
Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов времени. Значение 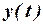 временного ряда формируется под влиянием сочетания длительных, кратковременных и случайных факторов. Факторы, действующие в течение длительного времени, оказывают определяющее влияние на изучаемое явление и формируют основную тенденцию ряда – тренд
временного ряда формируется под влиянием сочетания длительных, кратковременных и случайных факторов. Факторы, действующие в течение длительного времени, оказывают определяющее влияние на изучаемое явление и формируют основную тенденцию ряда – тренд 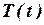 . Периодические факторы формируют сезонные колебания ряда
. Периодические факторы формируют сезонные колебания ряда 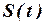 . Случайные факторы отражаются случайными изменениями уровней ряда
. Случайные факторы отражаются случайными изменениями уровней ряда 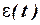 .
.
Аддитивная модель, в которой ряд представлен как сумма перечисленных компонент, имеет вид:
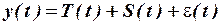 .
.
Модель, в которой ряд представлен как произведение перечисленных компонент, называется мультипликативной:
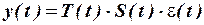 .
.
Из двух моделей указанного типа на основе анализа сезонных колебаний выбирается та, которая наиболее соответствует исходным статистическим данным.
Основная задача экономического исследования временного ряда состоит в том, чтобы выявить каждую из перечисленных компонент ряда. Так, при постоянной (или близкой к ней) амплитуде сезонных колебаний используется аддитивную модель; при существенно меняющейся (возрастающей или убывающей) амплитуде сезонных колебаний используется мультипликативную модель.
Для моделирования временных рядов используют модели парной линейной и нелинейной регрессии, множественной линейной и нелинейной регрессии и другие, специально разработанные модели.
3.2. Моделирование временных рядов с применением фиктивных переменных
Методические особенности построения модели временного ряда рассмотрим на примере ряда, учитывающую основную его тенденцию – тренд – и сезонные колебания с использованием фиктивных переменных.
Предположим, что сезонность можно учесть колебаниями моделируемой переменной по кварталам. Первый квартал каждого года будем считать эталонным кварталом, а для оценки различия между ним и другими кварталами будем использовать три фиктивные переменные. Тогда модель временного ряда представима в виде уравнения множественной линейной регрессии:
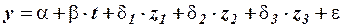 ,
,
где:
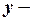 зависимая – объясняемая переменная;
зависимая – объясняемая переменная;
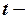 время;
время;
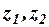 и
и 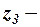 фиктивные переменные;
фиктивные переменные;
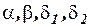 и
и 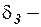 параметры уравнения регрессии;
параметры уравнения регрессии;
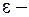 случайное слагаемое.
случайное слагаемое.
Фиктивные переменные, введенные в уравнение, определяются следующим образом:
| Переменная | 1 квартал | 2 квартал | 3 квартал | 4 квартал |
| z1 | ||||
| z2 | ||||
| z3 |
3.3. Автокорреляция уровней временного ряда
Между значениями временного ряда на отдельных его участках может иметь место корреляционная связь. Корреляционная зависимость между последовательными уровнями коэффициента автокорреляции временного ряда называется автокорреляцией уровней ряда.
Коэффициент автокорреляции порядка 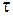 определяется как коэффициент корреляции между рядом
определяется как коэффициент корреляции между рядом 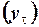 и рядом его смещенных значений
и рядом его смещенных значений 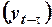 :
:
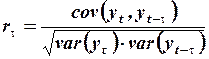 ,
,
где:
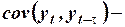 ковариация переменных
ковариация переменных 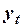 и
и 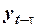 ;
;
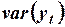 и
и 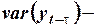 вариации переменных
вариации переменных 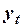 и
и 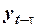 .
.
Число периодов 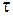 , для которого рассчитывается коэффициент автокорреляции, называется лагом. С увел
, для которого рассчитывается коэффициент автокорреляции, называется лагом. С увел
 2014-02-18
2014-02-18 403
403






