О.В.Громыко
Topic 12. Organizational Conflict and Negotiation
Organizational conflict is the discord that arises when the goals, interests, or values of different individuals or groups are incompatible and those individuals or groups block or thwart each other’s attempts to achieve their objectives.
Types of conflict:
- Interpersonal conflict is a conflict between individual members of an organization, occurring because of differences in their goals or values;
- Intragroup conflict is a conflict that arises within a group, team or department;
- Intergroup conflict is a conflict between groups and teams;
- Interorganizational conflict is a conflict that arises across organizations.
Sources of conflict:
- Incompatible goals and time horizons;
- Overlapping authority;
- Task interdependencies;
- Incompatible evaluation or reward system;
- Status inconsistencies.
Conflict management strategies:
Strategies focused on individuals:
- Increasing awareness of the sources of conflict;
- Increasing diversity awareness and skills;
- Practicing job rotation or temporary assignment;
- Using permanent transfers or dismissal when necessary.
Strategies focused on the whole organization:
- Changing an organization’s structure and culture;
- Altering the source of conflict.
Negotiation is a method of conflict resolution in which the 2 parties in conflict consider various alternative ways to allocate recourses to each other in order to come up with a solution acceptable to them both.
Distributive negotiation is adversarial negotiation in which the parties in conflict compete to win the most resources while conceding as little as possible.
Integrative negotiation is a cooperative negotiation in which the parties in conflict work together to achieve a resolution that is good for them both.
|
|
|
В настоящее время наиболее распространенным методом расчета сложных конструкций является метод конечных элементов (МКЭ). При его использовании конструкция, представляющая собой непрерывную среду, заменяется ее моделью, составленной из конечног
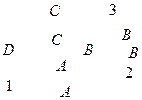 числа блоков – элементов, поведение каждого из которых может быть определено заранее. Взаимодействие элементов между собой позволяет описать общую картину деформирования системы.
числа блоков – элементов, поведение каждого из которых может быть определено заранее. Взаимодействие элементов между собой позволяет описать общую картину деформирования системы.
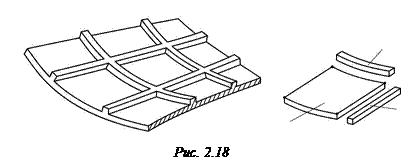
Например, оболочка, состоящая из гладкой панели и кольцевых и продольных подкреплений (рис. 2.18), может быть составлена из набора простых элементов: цилиндрической прямоугольной панели 1, прямого стержня 2, криволинейного стержня 3. Жесткости каждого из этих элементов должны быть определены заранее. На рисунке обозначены узловые точки А, В, С, D, по которым элементы собираются в общую систему. Напряженное состояние такой сложной конструкции может быть определено с помощью МКЭ с единых позиций.
С помощью МКЭ решено большое количество задач прочности, устойчивости и динамики конструкций. Он используется также для анализа нелинейных явлений, с его помощью удается решить сложные многомерные задачи оптимизации и т. п.
Основные достоинства МКЭ заключаются в его универсальности: возможности использовать элементы различных типов, произвольной геометрии рассматриваемой области, простоте приемов построения элементов высокой точности. В варианте метода, рассматриваемом ниже – методе перемещений, – при стыковке элементов требование удовлетворения естественных краевых условий необязательно.
Этот наиболее известный вариант МКЭ использует формулировку принципа возможных перемещений (см. главу 1).
|
|
|
В матричной форме для трехмерного тела принцип возможных перемещений можно записать следующим образом:
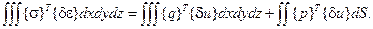
Перепишем это же соотношение иначе:
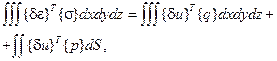 (2.77)
(2.77)
где векторы напряжений и деформаций соответственно равны:
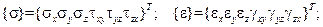 (2.78)
(2.78)
а векторы объемных, поверхностных сил и перемещений следующие:
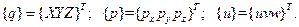 (2.79)
(2.79)
Соотношение (2.77) не зависит от свойств материала и справедливо как для линейной, так и для нелинейной системы. Если линейно-упругое тело имеет начальные деформации 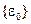 (например, температурные), то физические соотношения принимают вид
(например, температурные), то физические соотношения принимают вид
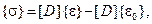 (2.80)
(2.80)
где [D] – матрица упругих констант, получаемая из (1.21) – (1.23).
Подставляя соотношения (2.80) в уравнение (2.77), получаем
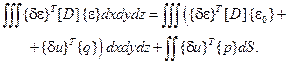 (2.81)
(2.81)
Выражение (2.81) справедливо как для отдельного элемента, так и для всей системы в целом. Будем полагать, что оно относится к каждому элементу и интегрирование ведется по объему и поверхности элемента. Формулировка принципа возможных перемещений для системы элементов в целом выглядит так:
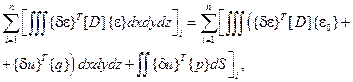 (2.82)
(2.82)
где n – число элементов, на которое разбито исследуемое тело.
МКЭ использует процедуры различных вариационных методов. В рассматриваемом варианте метода так же, как и в методе Рэлея – Ритца, необходимо задаться функцией перемещений, но не на всей области, а лишь в пределах элемента.
Функции перемещений задают в виде полиномов по степеням пространственных координат х, у, z:
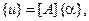 (2.83)
(2.83)
где [A] – матрица, зависящая от координат элемента; 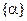 – вектор коэффициентов полиномиального разложения функций перемещений. Количество этих коэффициентов соответствует числу степеней свободы элемента, а сами коэффициенты связаны с узловыми перемещениями. Если обозначить вектор узловых перемещений элемента через
– вектор коэффициентов полиномиального разложения функций перемещений. Количество этих коэффициентов соответствует числу степеней свободы элемента, а сами коэффициенты связаны с узловыми перемещениями. Если обозначить вектор узловых перемещений элемента через 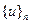 , то функцию перемещений можно описать выражением
, то функцию перемещений можно описать выражением
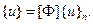 (2.84)
(2.84)
Воспользуемся соотношениями между деформациями и перемещениями (1.15). Подставляя в них зависимость (2.84), получим
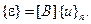 (2.85)
(2.85)
В дальнейших расчетах важное значение имеет матрица 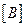 , которая устанавливает связь деформаций с узловыми перемещениями. Вектор напряжений определяют по физическим соотношениям (2.80), которые с учетом связи (2.85) принимают следующий вид:
, которая устанавливает связь деформаций с узловыми перемещениями. Вектор напряжений определяют по физическим соотношениям (2.80), которые с учетом связи (2.85) принимают следующий вид:
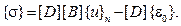 (2.86)
(2.86)
Правую и левую части условия равновесия (2.81) рассмотрим по отдельности. Подставляя вектор деформаций (2.85) в левую часть уравнения (2.81), выразим его через узловые перемещения и интеграл, который обозначим символом 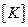 :
:
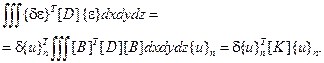 (2.87)
(2.87)
В этом соотношении 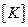 является матрицей, которая содержит информацию о поведении элементарного участка деформируемой системы. Это матрица жесткости элемента, являющаяся основной характеристикой системы в МКЭ.
является матрицей, которая содержит информацию о поведении элементарного участка деформируемой системы. Это матрица жесткости элемента, являющаяся основной характеристикой системы в МКЭ.
Интегралы по объему и по поверхности в правой части выражения (2.81) представим следующим образом:
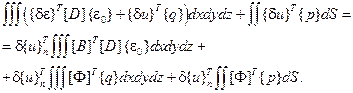 (2.88)
(2.88)
Так вычисляется вектор внешних сил 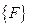 , приведенных к узлам.
, приведенных к узлам.
Если известны матрица 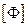 , которая связывает перемещения в любой точке элемента с узловыми перемещениями (2.84), и матрица
, которая связывает перемещения в любой точке элемента с узловыми перемещениями (2.84), и матрица 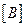 , входящая в соотношения между деформациями и перемещениями узлов элемента (2.85), то матрицу жесткости
, входящая в соотношения между деформациями и перемещениями узлов элемента (2.85), то матрицу жесткости 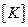 и вектор внешних узловых сил
и вектор внешних узловых сил 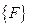 определяют по формулам:
определяют по формулам:
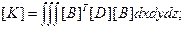 (2.89)
(2.89)
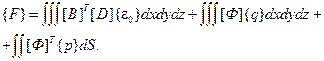 (2.90)
(2.90)
Таким образом, условие равновесия каждого элемента имеет вид
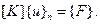 (2.91)
(2.91)
Соотношения для всей системы приводятся к аналогичной форме, но вместо вектора узловых перемещений 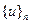 и матрицы жесткости
и матрицы жесткости 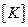 элемента следует подставить вектор узловых перемещений всей системы
элемента следует подставить вектор узловых перемещений всей системы 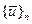 (глобальный вектор перемещений) и соответствующую матрицу
(глобальный вектор перемещений) и соответствующую матрицу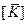 (общая или глобальная матрица жесткости):
(общая или глобальная матрица жесткости):
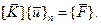 (2.91')
(2.91')
При расчете конструкций с помощью МКЭ уравнение (2.91') является основным, позволяющим определить перемещения (и, воспользовавшись соотношением (2.86)), напряженное состояние в каждом элементе системы. Основная задача расчета конструкций методом ко-
 нечных элементов заключается в определении матриц жесткости элементов, общей матрицы жесткости
нечных элементов заключается в определении матриц жесткости элементов, общей матрицы жесткости 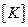 и вектора узловых сил
и вектора узловых сил 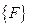 .
.
|
|
|
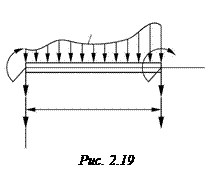 Пример. Рассмотрим элемент стержня (рис. 2.19), который нагружен поперечной распределенной нагрузкой
Пример. Рассмотрим элемент стержня (рис. 2.19), который нагружен поперечной распределенной нагрузкой 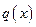 . Для этого элемента введем вектор
. Для этого элемента введем вектор 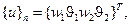 (2.92)
(2.92)
который состоит из двух узловых перемещений 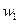 ,
, 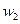 и двух углов поворота
и двух углов поворота 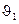 ,
, 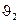 .
.
Функцию перемещений в элементе выразим алгебраическим полиномом, имеющим четыре коэффициента:
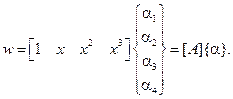 (2.93)
(2.93)
Учитывая, что сечение х поворачивается на угол 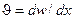 , и условия на границах (при
, и условия на границах (при 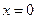 имеем
имеем 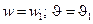 , а при
, а при 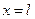 имеем
имеем 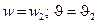 ), определим вектор узловых перемещений
), определим вектор узловых перемещений
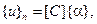 (2.94)
(2.94)
где матрица 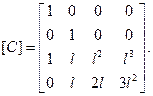
Очевидно, связь вектора коэффициентов 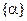 с узловыми перемещениями
с узловыми перемещениями 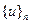 имеет вид:
имеет вид:
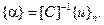
Если это соотношение подставить в выражение (2.93), получим
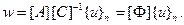 (2.95)
(2.95)
Для рассматриваемой задачи матрица-строка 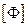 из уравнения (2.95) примет вид:
из уравнения (2.95) примет вид:
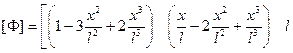
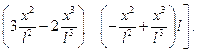 (2.96)
(2.96)
Для волокна, находящегося на расстоянии z от нейтральной оси стержня, относительное удлинение 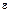 определяется зависимостью
определяется зависимостью
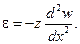
Учитывая соотношение (2.95), получим 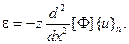
Вычислим матрицу 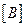 путем двойного дифференцирования каждой компоненты соотношения (2.96) и умножения полученного результата на
путем двойного дифференцирования каждой компоненты соотношения (2.96) и умножения полученного результата на 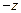 :
:
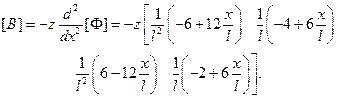
Наконец, на основе уравнения (2.91) определяем матрицу жесткости элемента стержня (примем, что модуль упругости и момент инерции в пределах элемента не изменяется):
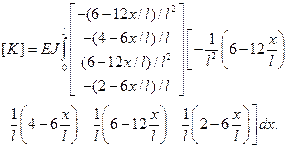
В результате перемножения матриц и интегрирования получим окончательное выражение для матрицы жесткости элемента стержня:
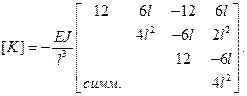 (2.97)
(2.97)
Вычисленная матрица 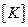 связывает вектор узловых сил, который включает четыре компоненты (см. рис. 2.19)
связывает вектор узловых сил, который включает четыре компоненты (см. рис. 2.19) 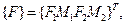 с вектором перемещений
с вектором перемещений 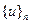 . Матрица (2.97) симметрична, поскольку это следует из условия взаимности работ теории упругости.
. Матрица (2.97) симметрична, поскольку это следует из условия взаимности работ теории упругости.
В случае нагруженного элемента (рис. 2.19) узловые силы определяются из выражения (2.90), которое для рассматриваемой задачи принимает вид
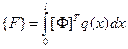
или, записывая покомпонентно векторы 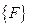 и
и 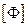 , получим:
, получим:
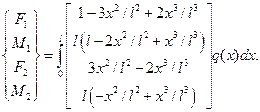
Если нагрузка 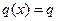 не изменяется в пределах элемента, то в результате интегрирования найдем вектор узловых сил для элемента:
не изменяется в пределах элемента, то в результате интегрирования найдем вектор узловых сил для элемента:
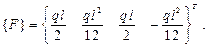 (2.98)
(2.98)
Он эквивалентен распределенной нагрузке, приложенной к балке.
Пример. Исследуем поперечный изгиб балки, вся длина которой – один конечный элемент. Для консольной балки длиной 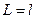 (рис. 2.20а) нагрузку q заменяем силой
(рис. 2.20а) нагрузку q заменяем силой 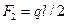 и моментом
и моментом 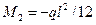 в соответствии с (2.98).
в соответствии с (2.98).
|
|
|
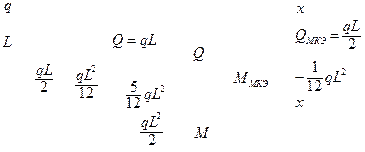
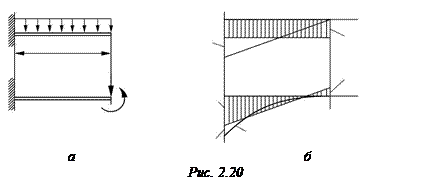
Вычислим перемещения этой эквивалентной системы с учетом условий закрепления левого края:
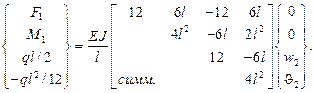
Конец стержня перемещается и поворачивается соответственно на
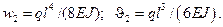
Для рассматриваемой балки точные решения по перемещению и углу поворота произвольного сечения имеют вид
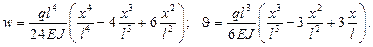
Таким образом, для узловой точки при 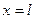 с помощью МКЭ получены точные значения.
с помощью МКЭ получены точные значения.
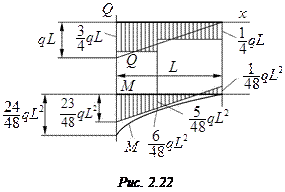
На рис. 2.20б построены точные и приближенные по МКЭ (с вертикальной штриховкой) эпюры изгибающих моментов 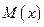 и перерезывающих сил
и перерезывающих сил 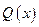 для балки. Очевидно, они существенно отличаются при использовании для решения задачи только для одного элемента. Увеличение частоты разбиения балки на элементы приводит к уменьшению разницы в эпюрах.
для балки. Очевидно, они существенно отличаются при использовании для решения задачи только для одного элемента. Увеличение частоты разбиения балки на элементы приводит к уменьшению разницы в эпюрах.
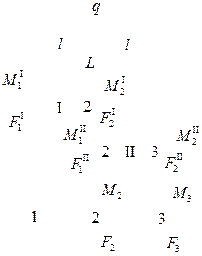
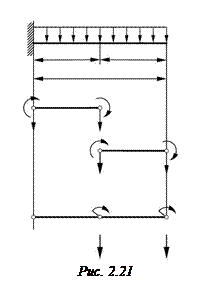
Теперь представим, что эта же балка состоит из двух элементов (рис. 2.21), длина каждого из которых 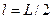 . Векторы перемещений и сил в этом случае имеют вид
. Векторы перемещений и сил в этом случае имеют вид
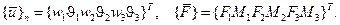
Ненулевые компоненты вектора { F } определим из (2.96):
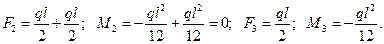
Матрицу жесткости системы из двух элементов получим из (2.97):
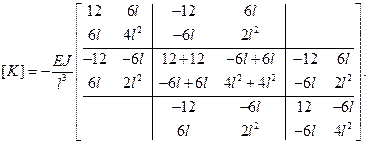
Она получена путем сложения двух частей, каждая из которых соответствует выражению (2.97), и смещенных друг относительно друга на две строки и два столбца. Для рассматриваемой системы векторы перемещений и сил имеют следующий вид:
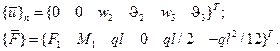
В результате решения уравнений убеждаемся, что получены точные значения для узловых перемещений 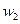 ,
, 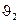 ,
, 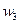 ,
, 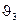 . Из эпюр моментов и перерезывающих сил (рис. 2.22) следует, что в этом случае усилия и моменты по МКЭ ближе к точным значениям. Опыт показывает, что при дальнейшем увеличении числа элементов (при более густой сетке) усилия и перемещения будут еще точнее.
. Из эпюр моментов и перерезывающих сил (рис. 2.22) следует, что в этом случае усилия и моменты по МКЭ ближе к точным значениям. Опыт показывает, что при дальнейшем увеличении числа элементов (при более густой сетке) усилия и перемещения будут еще точнее.
Метод конечных элементов существует во многих вариантах, причем наиболее распространенная схема в перемещениях представлена выше. Вариант, основанный на процедуре Галеркина, используется значительно реже. Если соотношение для полной потенциальной энергии механической системы записать сложно, он является особенно эффективным.
Особенности использования метода рассмотрим снова на примере поперечного изгиба балки. Дифференциальное уравнение изгиба балки постоянной жесткости имеет вид
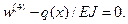
В рассматриваемой постановке вектор, аналогичный вектору узловых перемещений, должен иметь восьмой порядок, поскольку на каждом конце элемента в качестве степеней свободы необходимо принять не только перемещение и угол поворота, но и изгибающий момент и перерезывающую силу. Поскольку угол поворота соответствует первой производной 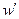 от перемещения, а момент и перерезывающая сила пропорциональны второй и третьей производным, вектор
от перемещения, а момент и перерезывающая сила пропорциональны второй и третьей производным, вектор 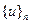 представим в виде
представим в виде
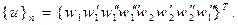
В этом случае функция перемещения в пределах элемента выражается полиномом седьмой степени
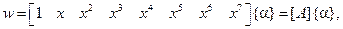
где вектор коэффициентов полинома содержит восемь компонент:
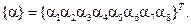
Учтем, что на границах при 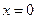 и
и 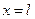 перемещение
перемещение 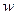 и производные от него равны узловым составляющим вектора
и производные от него равны узловым составляющим вектора 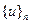 :
:
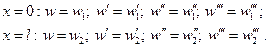
Последние соотношения позволяют записать связь между вектором узловых перемещений 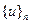 и вектором коэффициентов
и вектором коэффициентов  :
:
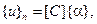
где
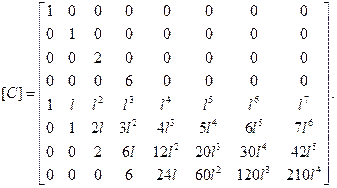
Итак, перемещение любой внутренней точки элемента через узловые перемещения и их производные выражается зависимостью
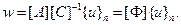
Подставляя ее в уравнение равновесия и учитывая, что выбранная функция-полином в общем случае не является его решением, получим функцию-ошибку
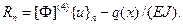
В соответствии с методом Галеркина функция-ошибка должна подчиняться соотношению (2.14), которое для случая МКЭ соответствует следующему выражению:
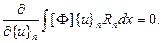
Эта зависимость позволяет построить матрицу жесткости и вектор внешних сил элемента, т. е. получить решение задачи.
Метод конечных элементов в варианте формулировки по методу Галеркина приводит к хорошим результатам для усилий и перемещений даже при небольшом числе элементов (крупной сетке), на которые делят деформируемую систему. Кажущаяся сложность вычислений по сравнению с методом, основанным на принципе возможных перемещений, компенсируется высокой точностью (особенно при определении внутренних усилий и моментов).
Решение двумерных задач методом конечных элементов. Исследование прочности и жесткости тонкостенных элементов конструкций во многих случаях сводится к решению двумерных задач. В некоторых случаях эти задачи удается свести к «квазиодномерным». Область интегрирования и граничные условия допускают возможности использования метода разделения переменных и преобразования функционала, зависящего от двух переменных, к одномерному. Указанный вариант решения задач используется достаточно часто, но, к сожалению, далеко не всегда возможен.
В случае сложных, нерегулярных областей с криволинейными границами используют двумерные элементы. Наиболее распространены плоские треугольные и прямоугольные элементы, комбинируя которые удается достаточно просто построить расчетные схемы самых сложных тонкостенных пространственных конструкций.
 Следуя изложенному выше алгоритму решения МКЭ, вначале необходимо построить матрицы жесткости элементов, составляющих расчетную схему. На примере плоской задачи теории упругости рассмотрим способ построения матрицы жесткости треугольных конечных элементов, а на примере поперечного изгиба пластин – прямоугольных.
Следуя изложенному выше алгоритму решения МКЭ, вначале необходимо построить матрицы жесткости элементов, составляющих расчетную схему. На примере плоской задачи теории упругости рассмотрим способ построения матрицы жесткости треугольных конечных элементов, а на примере поперечного изгиба пластин – прямоугольных.
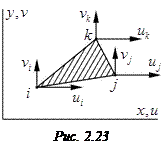
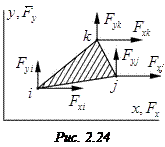
Треугольный элемент с тремя узловыми точками i, j и k приведен на рис. 2.23. Будем производить обход узлов от точки i к j и k против хода часовой стрелки. Функцию перемещений в элементе получим из условия, что линейные и угловые компоненты деформаций в нем постоянны.
Пусть
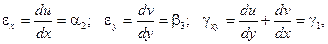 (2.99)
(2.99)
где 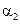 ,
, 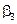 ,
, 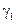 – константы. Интегрируя (2.99), найдем связи:
– константы. Интегрируя (2.99), найдем связи:
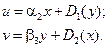
Подставляя их в третье уравнение (2.99), получим:
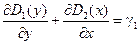 ,
,
где 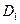 и
и 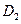 – некоторые независимые функции. Это уравнение превращается в тождество, если
– некоторые независимые функции. Это уравнение превращается в тождество, если
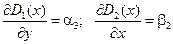 .
.
В результате интегрирования получим следующие зависимости:
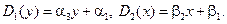
Таким образом, функция перемещения произвольных точек в элементе выражается линейно через их координаты:
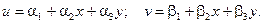 (2.100)
(2.100)
Отметим, что деформации в пределах каждого элемента являются постоянными. Очевидно, константы 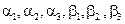 являются независимыми. Преобразуем соотношения (2.100) к матричной форме:
являются независимыми. Преобразуем соотношения (2.100) к матричной форме:
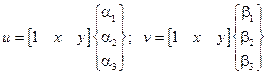 .
.
Выразим константы через перемещения и координаты узловых точек элемента. Запишем матричные соотношения:
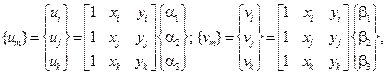
или 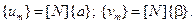
Тогда векторы, составленные из констант, выражаются так:
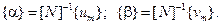
Теперь можно определить перемещения в любой точке элемента с помощью матричных соотношений:
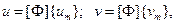 (2.101)
(2.101)
где 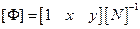 .
.
Таким образом, матрица связи перемещений в элементе с узловыми перемещениями в развернутой форме имеет вид:
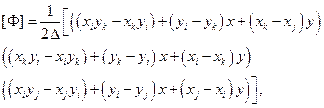
где 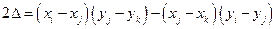 – удвоенная площадь треугольного элемента.
– удвоенная площадь треугольного элемента.
Как и ранее, размер вектора узловых перемещений 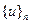 определяется произведением количества узлов в элементе и степеней свободы в узле, а вектора деформаций
определяется произведением количества узлов в элементе и степеней свободы в узле, а вектора деформаций 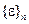 – размерностью задачи:
– размерностью задачи:
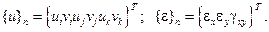 (2.102)
(2.102)
Запишем связь между ними через матрицу 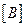 :
:
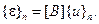
Для плоской деформации в соответствии с соотношениями (1.25)
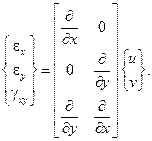
Подставляя в них зависимости (2.101) и учитывая, что узловые перемещения образуют вектор (2.102), получим выражение
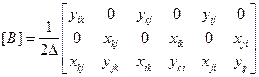 , (2.103)
, (2.103)
в котором 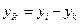 ,
, 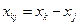 и т. д.
и т. д.
В случае плоского напряженного состояния матрица жесткости согласно (2.89) принимает вид
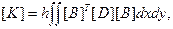 (2.104)
(2.104)
где h – толщина пластины.
Из (1.25) получим матрицу упругих констант для случая изотропного тела без учета температурного воздействия:
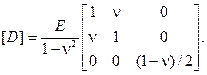 (2.105)
(2.105)
Если в выражение (2.104) подставить соотношения (2.103) и (2.105), получим матрицу жесткости конечного элемента треугольной формы для тела, которое находится в плоском напряженном состоянии
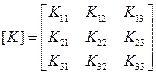 . (2.106)
. (2.106)
Здесь 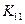 ,
, 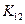 и др. – блоки размерностью
и др. – блоки размерностью 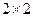 , которые зависят от координат вершин треугольника, жесткости
, которые зависят от координат вершин треугольника, жесткости 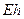 и коэффициента Пуассона, например:
и коэффициента Пуассона, например:
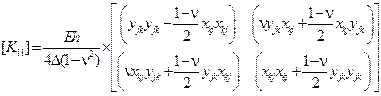 .
.
 Отметим, что для данного элемента при выводе матрицы жесткости
Отметим, что для данного элемента при выводе матрицы жесткости 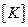 операция интегрирования упрощается, поскольку матрица
операция интегрирования упрощается, поскольку матрица 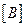 не является функцией от х и у, а зависит только от координат узловых точек.
не является функцией от х и у, а зависит только от координат узловых точек.
Векторы перемещений узлов и узловых сил в элементе (рис. 2.24) связаны через матрицу жесткости 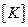 :
:
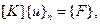
где 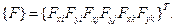 (2.107)
(2.107)
Если векторы перемещений и сил в каждой узловой точке представить в виде:
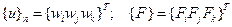 , где
, где
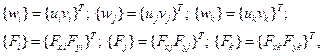
то в матрице (2.106), состоящей из блоков  и т. д., каждая составляющая определяет взаимодействие узловых сил и узловых перемещений в элементе.
и т. д., каждая составляющая определяет взаимодействие узловых сил и узловых перемещений в элементе.
Алгоритм построения глобальной (общей) матрицы жесткости системы проиллюстрируем на примере пластины, состоящей из нескольких треугольных элементов. На рис. 2.25 изображена пластина в форме трапеции.
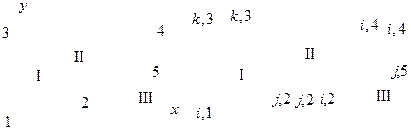
Разделим ее на три элемента, для каждого из которых запишем следующее матричное соотношение:
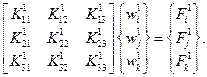
Верхние индексы будем относить к номеру элемента, т. е. для приведенного соотношения следует, что эта зависимость относится к пластине I (рис. 2.25). Аналогичные матричные уравнения запишем для треугольных элементов II и III:
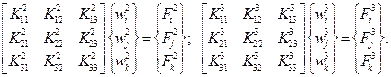
Каждый из узлов этих трех элементов, кроме номеров общей системы (1, 2, 3, 4, 5), имеет символы i, j, k. Поскольку перемещения в узлах смежных элементов равны, то справедливы условия
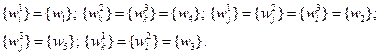
Что касается суммарных векторов усилий в каждом узле, то они равны:
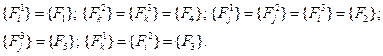
Суммируя составляющие матриц каждого элемента в соответствии с этими равенствами и заменяя обозначения векторов узловых перемещений элемента обозначениями векторов перемещений системы в целом, получим общее матричное уравнение плоской пластины, составленной из трех элементов:
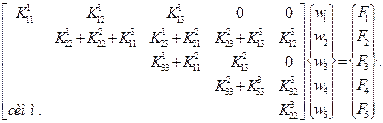 (2.108)
(2.108)
Так же, как и ранее, глобальная матрица жесткости системы симметрична, поскольку для одного и того же элемента 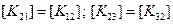 и т. д. Из уравнения (2.108) можно определить перемещения при заданных силах либо силы при известных перемещениях в узлах. Если, например, в результате закрепления пластины в точках 1 и 3 запрещены перемещения, а в точках 2, 4, 5 известны силы (рис. 2.25), то в уравнении (2.108) неизвестными являются векторы перемещений
и т. д. Из уравнения (2.108) можно определить перемещения при заданных силах либо силы при известных перемещениях в узлах. Если, например, в результате закрепления пластины в точках 1 и 3 запрещены перемещения, а в точках 2, 4, 5 известны силы (рис. 2.25), то в уравнении (2.108) неизвестными являются векторы перемещений 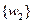 ,
, 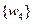 ,
, 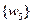 и сил
и сил 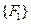 ,
, 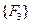 .
.
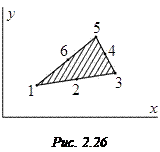 Отметим, что в рассмотренном варианте треугольного элемента напряжения и деформации на границе элементов не являются непрерывными функциями, а изменяются скачком. При малом числе элементов это приводит к большим погрешностям при расчете. Результат можно уточнить, применяя более густую сетку, т. е. разбивая систему на большее число элементов, или применяя элементы повышенной точности – с промежуточными точками. На рис. 2.26 показан элемент, имеющий не три, а шесть узловых точек. Функцию перемещений для него запишем следующим образом:
Отметим, что в рассмотренном варианте треугольного элемента напряжения и деформации на границе элементов не являются непрерывными функциями, а изменяются скачком. При малом числе элементов это приводит к большим погрешностям при расчете. Результат можно уточнить, применяя более густую сетку, т. е. разбивая систему на большее число элементов, или применяя элементы повышенной точности – с промежуточными точками. На рис. 2.26 показан элемент, имеющий не три, а шесть узловых точек. Функцию перемещений для него запишем следующим образом:
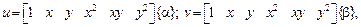 (2.109)
(2.109)
где векторы констант содержат по шесть компонент:
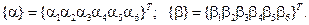
Матрицы жесткости этого элемента можно построить на основе того же самого алгоритма. Аналогичным способом определятся и глобальная матрица жесткости, а также деформации и напряжения. Если функцию перемещений выразить полиномами второй степени (2.109), то деформации и напряжения на границе элементов уже не будут изменяться скачком, т. е. не будут иметь разрывов. Решение можно получить еще более точным, если на грани элемента принять не одну, а две или более промежуточных точек. Размерность матриц жесткости при этом элемента увеличивается, они становятся более громоздкими. Но в связи с тем, что функции перемещений и напряжений выражаются более точными полиномами, то число элементов во всей системе можно значительно уменьшить, т. е. использовать более грубую (редкую) сетку.
На примере задачи поперечного изгиба пластин (рис. 2.27) рассмотрим еще один двумерный конечный элемент, имеющий прямоугольную форму в плане. Известно, что деформация упругой пластины определяется нормальными перемещениями и поворотами ее срединной поверхности (см. п. 2.1 и соотношения (2.2)).
Изображенный на рис. 2.27 прямоугольный элемент в углах на срединной поверхности имеет четыре узловые точки.

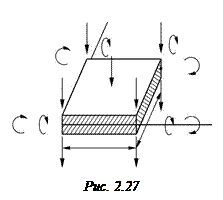 Предположим, что каждая точка может иметь независимое перемещение w (прогиб), а нормаль к срединной поверхности – две составляющие угла поворота:
Предположим, что каждая точка может иметь независимое перемещение w (прогиб), а нормаль к срединной поверхности – две составляющие угла поворота: 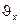 и
и 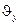 . Таким образом, общее число степеней свободы рассмат-риваемого прямоугольного элемента равно
. Таким образом, общее число степеней свободы рассмат-риваемого прямоугольного элемента равно 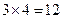 . Соответствующий вектор узловых перемещений состоит из двенадцати компонент:
. Соответствующий вектор узловых перемещений состоит из двенадцати компонент:
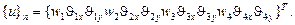 (2.110)
(2.110)
Функцию перемещений выразим через полином с двенадцатью коэффициентами:
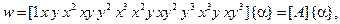 (2.111)
(2.111)
где 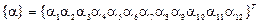 .
.
Очевидно, углы поворота нормали к срединной плоскости пластины при поперечном изгибе определяются соотношениями:
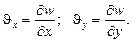 (2.112)
(2.112)
Учитывая условия на границах элемента, получим:
1) при 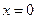 и
и 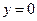
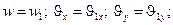
2) при 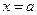 и
и 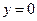
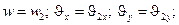
3) при 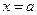 и
и 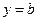
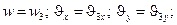
4) при 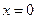 и
и 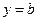
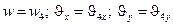 .
.
Используя соотношения (2.110) – (2.112), получим 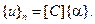
Тогда функция перемещений точек внутри элемента выражается через узловые перемещения соотношением:
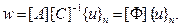 (2.113)
(2.113)
Отметим, что матрица-вектор 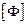 имеет размерность
имеет размерность 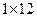 .
.
Если слой пластины удален от срединной поверхности на расстояние z, то деформации в нем выражаются линейной зависимостью
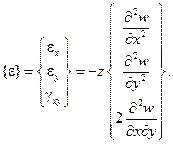
Подставляя в последнее выражение (2.113), получим зависимость
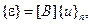 в которой
в которой 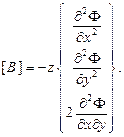 (2.114)
(2.114)
Если пластина выполнена из анизотропного материала (см. гл. 10) и ее свойства по толщине не изменяются, то
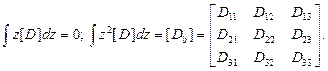 (2.115)
(2.115)
Для ортотропного материала, когда оси x и y совпадают с осями симметрии упругих свойств, жесткостные параметры 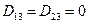 .
.
Если пластина выполнена из изотропного материала, то
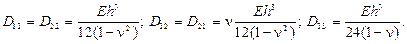 На основании общего выражения для матрицы жесткости конечного элемента (2.89), с учетом приведенных соотношений для жесткостных параметров, вычисляем матрицу жесткости элемента пластины
На основании общего выражения для матрицы жесткости конечного элемента (2.89), с учетом приведенных соотношений для жесткостных параметров, вычисляем матрицу жесткости элемента пластины
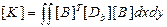 . (2.116)
. (2.116)
Преобразуем матричную запись к обычному виду, тогда, используя выражения (2.114) и (2.115), получим
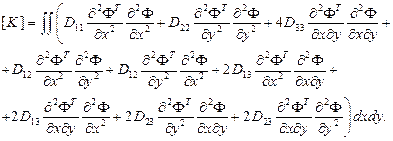
Это соотношение позволяет определить матрицу жесткости конечного элемента (имеющую размер 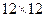 ) по известной матрице-строке [Ф] из выражения (2.113) и по имеющимся характеристикам изгибной жесткости пластины. Вектор узловых сил, который требуется для полного решения задачи, определяем из общей зависимости (2.90) для распределенной нагрузки р, нормальной к срединной поверхности:
) по известной матрице-строке [Ф] из выражения (2.113) и по имеющимся характеристикам изгибной жесткости пластины. Вектор узловых сил, который требуется для полного решения задачи, определяем из общей зависимости (2.90) для распределенной нагрузки р, нормальной к срединной поверхности:
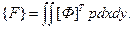
В рассмотренном нами случае был построен прямоугольный конечный элемент пластины с минимальным числом степеней свободы, так как при построении функции перемещений использовались лишь четыре угловых узла элемента. Если необходимо построить элемент повышенной точности (как в случае рассмотренной ранее плоской задачи), то в элементе следует ввести дополнительные узловые точки, что позволит повысить степень полинома, с помощью которого выражается функция перемещений (2.111). Отметим, что для моделирования сложных поверхностей двумерных тонкостенных элементов конструкций типа оболочек используются не плоские, а изогнутые конечные элементы с непрямыми границами. Их называют изопараметрическими конечными элементами. Они позволяют точнее описать реальную расчетную схему и получить результаты исследования напряженно-деформированного состояния с меньшей погрешностью.
 2014-02-24
2014-02-24 3575
3575