Общие определения. Реляционное исчисление

Реляционное исчисление

Реляционное исчисление лежит в основе декларативного подхода к формулировке запроса к БД, суть которого заключается в следующем:

Запросу к БД соответствует формула некоторой формально-логической теории, которая описывает свойства желаемого результата.

Ответом на запрос служит множество объектов из области интерпретации (которой является БД), на котором истинна формула, соответствующая запросу.

В качестве такой формально-логической теории используется теория исчисления предикатов первого порядка, в которой формула задается в виде предиката.

Понятие предиката

Даны некоторые попарно не пересекающиеся произвольные множества D₁, D₂, …, D_n, D_i Ç D_j = 0 для любых i ¹ j, и переменные x₁, x₂, …, x_n, принимающие значения из соответствующих множеств: x_i Î D_i для любых i.

Тогда предикатом (или предикатной функцией) называется функция P(x₁, x₂, …, x_n), принимающая одно из двух значений – 1 или 0 (истина или ложь).

Переменные x₁, x₂, …, x_n называются предикатными переменными. Множества D₁, D₂, …, D_n образуют область интерпретации предиката.

В записи предиката, наряду с логическими операциями Ù, Ú, Ø, смысл и использование которых традиционны, используются специальные операции – кванторы: всеобщности " и существования $. Смысл использования кванторов следующий:

" x (f(x)) означает, что для всех значений x из области интерпретации формула f(x) имеет значение "истина";

$ x (f(x)) означает, что существует по крайней мере одно значение x из области интерпретации, для которого формула f(x) имеет значение "истина".

Примеры

Пусть переменная x определена на множестве "учебная группа"; f(t) – утверждение
" t получает стипендию"; тогда предикат $ x (f(x)) имеет значение "истина", если хотя бы один член группы (не важно, кто именно) получает стипендию, и ложь, если никто в группе не получает стипендию.

Пусть переменная x определена на множестве "учебная группа"; f(t) – утверждение
" t не имеет задолженностей в сессию"; тогда предикат " x (f(x)) имеет значение "истина", если все члены группы не имеют задолженностей в сессию, и ложь, если хотя бы один член группы имеет задолженность.

Использование кванторов определяет понятие свободного и связанного вхождения переменных в предикатной формуле.

Вхождение переменной t в формулу y связано, если переменная t находится в формуле y в подформуле, начинающейся кванторами " или $, за которыми непосредственно следует переменная t; тогда о кванторе говорят, что он связывает переменную t. В остальных случаях t входит в y свободно.

Рассмотрим следующий пример:

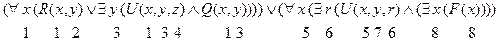
В примере пронумеровано использование переменных, в соответствии с их появлением в кванторах и в формуле. В соответствии с этим, в первой подформуле все вхождения x (помеченные цифрой 1) связаны, первое вхождение y (помеченное цифрой 2) свободно, следующие вхождения y (помеченные цифрой 3) связаны, вхождение переменной z (помеченное цифрой 4) свободно. Во второй подформуле все вхождения переменной x (помеченные цифрами 5 и 8) связаны, вхождение y (помеченное цифрой 7) свободно и, наконец, вхождение переменной r (помеченное цифрой 6) связано.

Кванторы в реляционном исчислении определяют области значений и видимости переменных. Это означает следующее:

Все переменные, входящие в формулу, при построении которой не использовались кванторы, являются свободными. Это означает, что если для какого-то определенного набора свободных переменных при вычислении предикатной формулы получено значение "истина", значит, этот набор значений свободных переменных войдет в результат, определяемый предикатом.

Если же вхождение переменной в формулу связано квантором, тогда такая переменная не видна за пределами формулы, связавшей эту переменную. При вычислении значения такой формулы используется не одно значение переменной, что имеет место для свободных переменных, а все значения из области определения данной переменной.

Рассмотрим пример. Пусть дано множество десятичных цифр D = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; тогда подмножество, состоящее из четных цифр, можно определить следующим образом: множество всех значений y, таких, для которых выполняется условие: $ x (x ¸ 2 = 0 Ù y = x).

Приведенный предикат интерпретируется следующим образом: существует хотя бы одно значение x Î D, которое четно и совпадает со значением некоторой свободной переменной y. Следовательно, если свободная переменная y имеет конкретное значение, например, 6, приведенный предикат будет иметь значение "истина", и значение переменной y входит в результат. Если же переменная y будет иметь значение 7 или 12, тогда предикат будет иметь значение "ложь", и данное значение y не войдет в результат.

В реляционном исчислении областью интерпретации предиката является база данных – т.е. множество всех значений всех доменов, на которых определены все схемы отношений, определяющие схему базы данных. Соответствие между предикатом P и отношением r(A₁, A₂,..., A_n) заключается в следующем:

Если P(a₁, a₂,..., a_n) = 1, то < a₁, a₂,..., a_n > есть выборка отношения r(A₁, A₂,..., A_n), т.е.

<a₁, a₂, …, a_n> Î r;

Если P(b₁, b₂,..., b_n) = 0, то <b₁, b₂, …, b_n> Ï r.

Таким образом, базисными понятиями исчисления являются понятие переменной и понятие правильно построенной формулы.

В зависимости от того, как определяется область значений используемых переменных, различают два вида реляционного исчисления:

Реляционное исчисление с переменными-кортежами, для которого областями определения переменных являются отношения БД, т.е. допустимым значением каждой переменной является кортеж некоторого отношения;

Реляционное исчисление с переменными на доменах, для которого областями определения переменных являются домены, определяющие множество допустимых значений атрибутов.

Правильно построенные формулы служат для выражения условий, накладываемых на переменные (кортежи или на доменах).