Формальное определение алгоритма

Таблица 3.1.

Перечень натуральных операций

Номер группы	Название операции	Описание
I	a - генерация	Преобразование пустого слова в однобуквенное слово состоящее из буквы a
Аннигиляция	Преобразование однобуквенного слова в пустое слово
II	Нахождение начала слова	Преобразование непустого слова в квазислова путем выделения его начала
III	Продвижение вперед	Перенос в квазислове выделяющей связи на одну букву правее
Продвижение назад	Перенос в квазислове выделяющей связи на одну букву левее
Удлинение вперед (без продолжения)	Преобразование квазислова с выделенным концом путем присоединения буквы, одинаковой с выделенной
Отбрасывание конца	Преобразование квазислова в новое путем отбрасывания букв, следующих за выделенной, которая при этом становится выделенной
IV	Отключение	Квазислово преобразуется в непустое слово путем отбрасывания выделяющей связи
V	Натуральные условия: Условие непустоты	Проверяется предикат «рассматриваемое слово непусто»
Условие начала	Проверяется предикат «в рассматриваемом квазислове выделена первая буква»
Условие конца	Проверяется предикат «в рассматриваемом квазислове выделена последняя буква»
Условие тождества букв	Проверяется предикат «в рассматриваемом квазислове выделена буква, одинаковая с a»

Итак, предположим, что некоторая конечная совокупность предметов перенумерована числами

1,2,...,n, n>1.

Такая совокупность упорядочена. В ней всегда можно просмотреть все ее предметы, выбрав сперва 1-й, а затем, переходя от одного к другому, в порядке их номеров. Существует алгоритмический процесс получения всех возможных нумераций по заданной нумерации, а значит, и алгоритм в интуитивном смысле для выполнения этой операции. Он заключается в следующем.

1) Составим строку s из одного элемента 1; перейдем к п.2.

2) Параметру j присвоим (временно) значение 1; перейдем к п.3.

3) Если j=n, то перейдем к п.4, иначе - к п.6.

4) Припишем в конце каждой из имеющихся последовательностей s число j+1. Нами получены новые последовательности, обменивая в каждой из них элемент j+1 столько раз, сколько возможно, с предыдущим элементом, из каждой новой последовательности получим еще j новых последовательностей. Каждую из новых последовательностей будем называть именем s (старых последовательностей уже нет). Перейдем к п. 5.

5) Увеличим значение j на 1 и перейдем к п. 3.

6) Образуем пары из полученных последовательностей, в каждой из которых 1-v членом является последовательность 1,2,...,n. Всего таких пар будет v=n!-1. Считаем, что в каждой паре элементы (числа), одинаково расположенные в ее членах, взаимно-однозначно соответствуют друг другу. Таким образом, получено v целочисленных функций, каждая из которых позволяет преобразовать исходную нумерацию в некоторую новую. Перейдем к п. 7.

7) Последовательно применяя полученные функции к исходной нумерации, получаем из нее (и кроме нее) еще v новых нумераций. Процесс окончен.

Существенной чертой описанного процесса является то обстоятельство, что кроме описания его и исходной нумерации для получения всех возможных нумераций никаких дополнительных данных не нужно. Полученные нами функции мы строим тогда, когда они могут потребоваться. Иметь их в запасе не нужно. Это важно потому, что такой запас, пригодный на любой случай, был бы бесконечен, а процедура получения всех возможных нумераций не была бы эффективной. При n=1 заданная нумерация есть единственно возможная.

Линеаризацией называется операция, с помощью которой произвольная конструкция класса (А,В,Е) преобразуется в слово определенного специального вида в специальном расширении алфавита А. Прежде всего опишем нужное нам расширение алфавита А.

Возьмем произвольный алфавит букв С, не пересекающийся ни с А, ни с В, и имеющее число букв, равное определенному нами максимальному рангу связей, перечисленных в В. Наконец, возьмем алфавит D, не пересекающийся ни с А, ни с В, ни с С, число букв которого равно 3. Для определенности буквами в D будем считать символы "(",")" и "1", которые будем называть скобками и единицей (цифрой 1). В качестве расширения алфавита А возьмем А'=ВÈАÈ СÈD. Слова, образованные из единиц, мы будем при выполнении нумераций применять как записи целых чисел в единичной системе счисления.

В дальнейшем, если некоторая буква предшествует в алфавите другой букве, будем говорить, что она младше этой второй буквы.

Ниже, при описании процесса линеаризации, мы будем произвольно нумеровать те или другие элементы конструкции, а затем учитывать все возможные результаты произвольной нумерации. Для этого будем репродуцировать обрабатываемую конструкцию n!-1 раз (где n - наибольший из произвольных номеров) и производить преобразование произвольных номеров (представленных как строки вида 1...1) способом, описанным выше. После каждого такого шага число обрабатываемых конструкций будет увеличиваться. Дальнейшие действия будут применяться к каждой из n! полученных конструкций в предположении, что каждая из них имеет то же имя, что и исходная.

Линеаризация состоит из следующих этапов.

Этап I. Преобразуемую конструкцию К заключают в оболочку.

Этап II. Находят в К для каждой буквы b_i (i=1,2,...) алфавита В' все связи, отвечающие этой букве. Производят их произвольную нумерацию и помечают словами 1,11, и т.д. Если произвольная нумерация привела к наибольшему номеру, который ³2, то определяют все возможные нумерации, увеличивая число экземпляров обрабатываемой конструкции и преобразуя вышеописанным способом номера. Считают, что каждая из полученных конструкций имеет имя К. Далее, переходя от связи к связи в каждой К, в порядке, который задают приписанные связям номера, упорядочивают ветви каждой связи аналогично тому, как это делалось для связей, с той лишь разницей, что вместо алфавита В используют алфавит С, считая, что ветвям i-ого жанра отвечает i-ая буква этого алфавита. Число конструкций снова возрастает (после каждой произвольной нумерации), а имя К закрепляется за каждой из полученных конструкций (это позволяет, говоря о К, иметь в виду каждую из них).

После окончания этого этапа все связи и ветви связей в некотором числе конструкций, каждая из которых называется К, помечены буквами и номерами.

Описанием каждой ветви любой связи называют слово, в начале которого стоит буква в В, затем несколько букв "1", затем - буква в С и, наконец, опять несколько единиц, Считают, что связи распались на отдельные ветви.

Этап III. В преобразуемой конструкции находят оболочку, внутри которой нет других оболочек. Пусть К' - заключенная в ней конструкция. Выписывают все конструктивные элементы, из которых образована К', в произвольном порядке, а перед каждым из них в лексикографическом порядке выписывают описания ветвей связей, для которых данный конструктивный элемент является связуемым объектом. Конструктивным элементом может быть (при повторных выполнениях этапа IV) либо буква в А, либо слово в А', заключенное в скобки. Конструктивный элемент со всеми предшествующими ему описаниями ветвей назовем фрагментом. Каждый фрагмент является словом в А'. Все выписанные фрагменты в лексикографическом порядке объединим в одно слово и заключим в скобки. Полученным результатом в К заменим К' вместе с содержащей ее оболочкой. Все ветви связей, которые прежде связывали оболочку, объемлющую К', теперь отнесем к открывающей скобке. Заметим, что если К' является пустой, то и слово, составленное из фрагментов, будет пустым.

Слово, которое будет получено после многократного выполнения данного этапа над каждой К и после отбрасывания содержащих его открывающей и закрывающей скобок, является одним из предварительных результатов, совокупность которых будет конечна.

Этап IV. Из всех предварительных результатов выбирают один, который лексикографически не старше остальных. Это и есть результат линеаризации.

Несмотря на ряд актов произвола, которые были произведены при линеаризации, ее результат однозначен, конечно, при заданных алфавитах В, С и D.

Делинеаризацией называется процесс восстановления конструкции по слову, имеющему соответствующую структуру, коротко говоря, - являющемуся ее описанием.

Для конструкции класса (А,В,Е) называются одинаковыми, если они при одинаковом А' дают один и тот же результат линеаризации.

Первичные алгоритмы. Предположим, что задан некоторый формальный язык L₁, предложения которого являются исходными данными, для преобразований, определяемых ниже. L₂ будем называть входным языком операндов. Предположим, что нам задан конечный набор операций, из которых некоторые могут быть применены к некоторым предложениям (символьным конструкциям) языка L₁. Операции будем делить на действия и условия. Выполнение действия заключается в том, что конструкция-операнд заменяется конструкцией, получаемой из этого операнда путем выполнения операции; то, что получится, в дальнейшем считается операндом. Если операция к исходному операнду не применима, то никакого результата не получается и никакая информация о его отсутствии не вырабатывается. Выполнение условия заключается в проверке, справедливо ли оно для операнда, или нет. В первом случае результатом проверки является логическое значение истина, во втором - ложь. Операнд остается неизменным. Условия являются предикатами.

Построим контекстно свободный язык L₂, который будем называть алгоритмическим. Для этого воспользуемся нотацией Бекуса. Предложение языка L₂ будем обозначать метасимволом (запись первичного алгоритма):

<запись первичного алгоритма>::= <безусловный приказ> ï <условный приказ>

<безусловный приказ>::= <метка> <разделитель I> <знак действия> <разделитель II> <отсылка> <разделитель III>

<условный приказ>::= <метка> <разделитель IV> <знак условия> <разделитель V> <отсылка> <разделитель VI> <отсылка> <разделитель III>

<отсылка>::= <метка> ï <стоп>

Для того чтобы L2 был полностью определен, необходимо задать с помощью метаформул значения метасимволов:

<метка> <разделитель IV>

<стоп> <разделитель V>

<разделитель I> <разделитель VI>

<разделитель II> <знак действия>

<разделитель III> <знак условия>

Мы этого не будем делать, определяя тем самым не один язык, а класс языков. В качестве L₂ может быть принят любой из конкретных языков этого класса. Заметим только, что разделители должны быть выбраны так, чтобы они однозначно разделяли приказы на соответствующие части, а разделитель III должен быть отличим от разделителя VI, а также от любой отсылки и метки.

Для того, чтобы наделить запись первичного алгоритма смыслом, зададим следующее правило.

П р а в и л о выполнения первичного алгоритма.

1) Просматривая запись первичного алгоритма с начала, найти первый приказ; перейти к п.2.

2) Если рассматриваемый приказ является безусловным, перейти к п.3, иначе к п.5.

3) Применить операцию, соответствующую знаку действия данного приказа, к операнду; найти отсылку в данном приказе; перейти к п.4.

4) Если выбранная отсылка имеет вид <стоп>, то процесс окончен; иначе, просматривая запись алгоритма с начала, найти приказ, метка которого одинакова с отсылкой, и перейти к п.2.

5) Если операнд удовлетворяет условию, соответствующему знаку условия данного приказа, то перейти к п.6, иначе - к п.7.

6) Найти первую отсылку данного приказа; перейти к п.4.

7) Найти вторую отсылку данного приказа; перейти к п.4.

Заметим, что правило выполнения зависит от языка L₂ и от заранее выбранного набора операций. Это правило является алгоритмом в интуитивном смысле слова, однако сформулированным настолько точно, что при его выполнении не может возникнуть никаких неясностей.

Запись первичного алгоритма, рассматриваемая вместе с правилом его выполнения, называется первичным алгоритмом.

Применение правила выполнения первичного алгоритма к совокупности, образованной из записи первичного алгоритма и записи операнда, порождает процесс, называемый алгоритмическим. Этот процесс может либо заканчиваться при выполнении п.2 правила, и тогда полученный операнд называется искомым результатом, либо обрываться из-за невыполнимости какого-либо другого пункта правила (безрезультатно остановиться), либо продолжаться неограниченно (не останавливаться).

В первом случае говорят, что первичный алгоритм применим к данному операнду, а во втором и третьем случаях - что неприменим.

Следует обратить внимание на то, что алгоритмический процесс представляет собой процесс совместного преобразования совокупности записей алгоритма и операнда. Частной особенностью этого преобразования является неизменность символьной конструкции, являющейся записью алгоритма.

Натуральные алгоритмы. Натуральными алгоритмами называются первичные алгоритмы, для выполнения которых требуется только знание натуральных операций и, может быть, линеаризации и делинеаризации. Приведем одно из семейств натуральных алгоритмов.

Пусть язык операндов L₂ имеет в качестве предложений только слова в алфавите А. Будем считать, что заданием этого алфавита определен грамматический класс <буква в А>. Будем считать, что, кроме того, для задания L₂ требуется единственная формула Бекуса <операнд>::=<буква в А> ï <операнд> <буква в А>

Алгоритмический язык L₁ конкретизируем следующим образом:

<метка>::= <цифра>ï<метка> <цифра>

<цифра>::= 0ï1ï2ï3ï4ï5ï6ï7ï8ï9

<стоп>::= -

<разделитель I>::=:

<разделитель II>::=:

<разделитель III>::=;

<разделитель IV>::=:

<разделитель V>::=:

<разделитель VI>::= /

<знак действия>::= h <буква в А> ïDï*ï®ï¬ï­ï¯ï! <буква в А>

<знак условия>::= Ñïнïк=<буква в А>

Смысл знаков действий и знаков условий разъясняет табл.3.2.

Приказы алгоритмического языка могут иметь вид

<метка>:<знак действия>:<отсылка>;

или <метка>:<знак условия>:<отсылка>/<отсылка>;

Таблица 3.2.

Знаки натуральных операций

Название операции	Знак	Название операции	Знак
a - генерация	ha	замена буквы на α	!α
аннигиляция	Δ	отключение	x
нахождение начала слова	*	линеаризация	l
продвижение вперед	→	делинеаризация	d
продвижение назад	←	условие непустоты	Ñ
удлинение вперед	↑	условие начала	н
отбрасывание конца	↓	условие конца	к

Для построения грамматик языков L₁ и L₂ достаточно знания операции конкатенации. Таким образом, построенный нами класс первичных (натуральных) алгоритмов, использующих только натуральные операции, линеаризацию и делинеаризацию, определен математически вполне строго.

Широкое формальное определение алгоритма. Мы знаем уже, что класс первичных алгоритмов задан, если заданы два языка: L₁ и L₂, причем предложения первого из них объявлены записями алгоритмов, а предложения второго - записями операндов и, если задано правило выполнения первичных алгоритмов, применимое к парам: запись алгоритма, запись операнда.

Первый пункт общего определения алгоритма гласит:

1) Первичные алгоритмы - это алгоритмы.

Но общее понятие алгоритма существенно шире. Его второй пункт гласит:

2) Если заданы два языка L₁ и L₂, причем предложения первого объявлены записями алгоритмов, а предложения второго - записями операндов, и если задан некоторый алгоритм W, операндами которого являются конструкции, получаемые связыванием каждого предложения из L₁ с n предложениями языка L₂ при помощи вполне определенной связи ранга n+1, то задано семейство n-местных алгоритмов.

Наконец, третий пункт общего определения гласит:

3) n-местные алгоритмы - тоже алгоритмы.

Таким образом, каждый алгоритм в широком формальном смысле, если он не первичный, имеет свой алгоритм выполнения. Если бы не были определены первичные алгоритмы, то невозможно было бы дать строгое определение и остальных алгоритмов, так как невозможно было бы указать ни одного алгоритма выполнения. Но после того, как построен хотя бы один алгоритм выполнения, можно строить многие другие, уже не привлекая первичных алгоритмов.

Одноместным называется n-местный алгоритм, для которого n=1. Первичные алгоритмы тоже будем называть одноместными.

Алгоритм в широком формальном смысле называется применимым к данному конкретному операнду (набору операндов), если алгоритм его выполнения применим к соответствующей символьной конструкции, объединяющей записи алгоритма и операнда (операндов). В противном случае говорят, что алгоритм в широком формальном смысле неприменим а данному операнду (набору операндов).

Два алгоритма называются функционально эквивалентными, если их языки операндов совпадают между собой и если всегда для одного и того же исходного данного оба алгоритма либо дают один и тот же результат, либо оба к нему неприменимы.

Т е о р е м а. Для всякого семейства первичных алгоритмов (определяемого двумя языками L₁ и L₂ и правилом выполнения) существует алгоритм в широком формальном смысле, который эквивалентен правилу их выполнения и имеет запись, графически тождественную с записью этого правила.

Такой алгоритм естественно назвать алгоритмом выполнения для данного семейства первичных алгоритмов. Приведенная теорема, хотя и не позволяет при определении понятия алгоритма отказаться от определения первичных алгоритмов, все же "уравнивает в правах" первичные алгоритмы с непервичными.

Нередко возникает необходимость применять одни алгоритмы к записям других. Для того, чтобы иметь при этом возможность пользоваться формулами, применяемыми в других математических дисциплинах, нужно соблюдать специальные предосторожности. Обычно алгоритмы обозначают латинскими буквами; их записи обозначают теми же буквами с крышкой (черточкой) наверху; определяемые ими функции обозначают теми же буквами с волной наверху. Например, если g - алгоритм, то 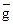- его запись, а 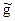- порождаемая им функция (операция, отображение).

При соблюдении вышеуказанных предосторожностей можно следующим образом описать связь между алгоритмом, отвечающими ему языками и алгоритмом выполнения.

Пусть L₂={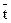} - алгоритмический язык, L₁={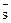} - язык операндов, z - связь (n+1)-ого ранга и W - алгоритм выполнения. Обозначим через 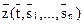конструкцию, получаемую путем связывания 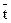языка L₂ и n предложений 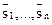языка L₁. Тогда равенство 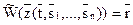означает, что t является алгоритмом и что 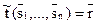. При этом 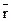- запись искомого результата.

Для каждого семейства алгоритмов, определяемого некоторым алгоритмом выполнения W, множество L₃={r} записей всех возможных искомых результатов является формальным языком. Таким образом, каждому семейству алгоритмов отвечает еще один формальный язык: язык искомых результатов. В частном случае он может быть подмножеством языка операндов.

Рассмотрим два семейства алгоритмов, у которых эквивалентны алгоритмы выполнения. Ясно, что эти семейства имеют одни и те же языки операндов, искомых результатов и алгоритмический. Возьмем два алгоритма, принадлежащих разным семействам, но имеющих одну и ту же запись. Такие алгоритмы эквивалентны, но при выполнении порождают неодинаковые процессы.

О п р е д е л е н и е. Два алгоритма, которые имеют одинаковые записи и эквивалентны, являются одним и тем же алгоритмом (или экземплярами одного и того же алгоритма).

Теперь нетрудно уточнить приведенное выше общее определение алгоритма (вернее, дополнить его).

Алгоритм - это совокупность записи алгоритма и отображения, индуцируемого его алгоритмом выполнения.