Регрессионный анализ

Анализ используется для математического описания (аппроксимации) связи выявленные на стадии корреляции, с помощью каких-либо функций.

Наиболее распространены уравнения:

1. Прямой y_i = a + b×х

2. Гиперболы y_i = a + b×1/х_i

3. Квадратичной параболы y_i = a + b× х_i + c× х_i²

4. Кубической параболы y_i = a + b× х_i + c× х_i² + d× х_i³

5. Логарифмические y_i = a + b× lg х y_i = a + b× ln х

6. Степенные y_i = a + b^хi

7. Показательные (экспоненты) y_i = a + x^b

8. Тригонометрические

8.1. синусоида y_i = a + b× Sin х_i + c× Sin х_i²

8.2. косинусоида y_i = a + b× Cos х_i + c× Cos х_i²

х – обязательно брать в радианах.

При парной корреляции и прямолинейной зависимости параметры уравнения прямой а и b находят решая совместную систему нормальных уравнений:

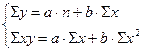
Есть готовые уравнения

b – коэффициент регрессии, показывает на сколько единиц изменяется у если х изменяется на единицу.

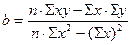
а – свободный член уравнения, показывает чему равен у если х = 0, но экономическую интерпретацию надо давать с большой осторожностью четко представляя взаимосвязь анализируемых явлений.

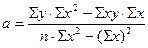
Для криволинейных зависимостей параметры уравнений а b c d и т.д. обычно определяются по стандартным программам ЭВМ; задача решается методом ведущих элементов Карла Гаусса, в основу положен метод наименьших квадратов.

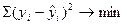
Для криволинейных связей параметры a и b определяются примерно также как и для прямой, но сначала функция приводится к линейному виду (линеаризируется).

Пример:

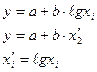
Определив параметры а и b производим обратное действие (потенцирование), получая истинные значения а и b.

Кроме того для квадратичной параболы, степенной, логарифмической есть готовые формулы.

Для гиперболы берем не 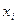, а 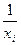и сразу получаем параметры а и b. Уравнение прямой – единственное, а криволинейную связь можно описать несколькими функциями.

18.10.00 10:09:22

Для выбора одной из них ориентируемся на минимум одного из трех статистических критериев.

1. Точность аппроксимации
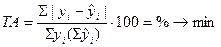
2. Минимум остаточной дисперсии
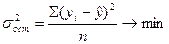
3. Среднее квадратичное отклонение по линии регрессии

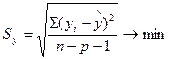
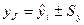
n – число наблюдений;

р – число факторов одновременно введенных в исследование;

n - p - 1 – число степеней свободы т.е. число неповторяющихся сочетаний между у и х.

После выбора по статистическим критериям криволинейной функции, по критерию Блэкмана определяем, что предпочтительнее – уравнение кривой или прямой.

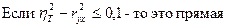
Если по критерию Блэкмана получим значение не немного превышающее 0,1 то проверку существенности расхождений выполняем по Z -критерию Фишера.

Если Z < 2 то разница не существенна и выбираем прямолинейную форму связи.