Корреляционый анализ

Зерно

БАЛАНСОВЫЙ МЕТОД

МЕТОД СРАВНЕНИЯ

С помощью относительных, абсолютных, средних величин и индексов показатели анализируемого периода сравниваем:

- с планами;

- с показателями предшествующих периодов;

- с показателями родственных предприятий;

- со средними показателями по отрасли;

- с лучшими отечественными и зарубежными предприятиями;

- с идеальной моделью.

Основан на соизмерении средств и их источников, ресурсов и потребителей.

В Р.Ф. составляется ежегодно около 5 тыс. балансов. Половина из них – транспортные. Кроме того составляются материальные балансы, балансы по труду, финансовые балансы – бюджет.

Баланс имеет приходную и расходную часть.

Пример:

Приход: валовый сбор определяем как произведение урожайности на посевную площадь.

Расход:

а) семенной фонд;

б) корм скоту;

в) расчет с работниками;

г) переработка на местных предприятиях;

д) выполнение договорных обязательств.

Затем сравниваем приходную и расходную части, если получили «+», то район избыточен; а если «-», то район дефицитный.

Затем составляется шахматная таблица по регионам и поставщики прикрепляются к потребителям на основе критерия оптимизации.

Затем составляется корреспонденция перевозок.

Корреляция-это соотношение, соотнесение.

Используется для установления наличия и численной оценки силы (тесноты) связи между явлениями.

Связи делятся на детерминированные и статистические.

Детерминированные связи - простые, всеобщие и выступают в виде физических и естественных законов.

Статистические связи – сложны, многообразны, всегда не полны и носят вероятностный характер, выступая в виде тенденций и закономерностей.

Корреляция бывает парная y = f (x) и множественная y = f (x₁;x₂;…x_n)

Оценка силы связи между явлениями производится с помощью десяти коэффициентов, в той или иной степени отражающих статистические взаимосвязи.

1. Коэффициент корреляции рангов Кендалла
2. Критерий согласия Р. Пирсона (Х²)
3. Критерий Фехнера
4. Z-критерий Р. Фишера
5. Критерий Романовского
6. Критерий Колмогорова
7. Критерий Ястремского
8. Коэффициент корреляции
9. Теоретическое корреляционное отношение
10. Критерий Блэкмана

В простейшем случае парной корреляции и прямолинейной формы связи, силы её оцениваем с помощью коэффициента парной корреляции

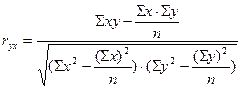где:

х_i – конкретное значение признака – фактора

у_i – соответствующее значение результативного признака

n – число пар наблюдений

r_yx – коэффициент корреляции может изменяется от 0 до ± 1

0 – прямолинейной связи нет

1 – связь прямая функциональная

-1 – обратная функциональная связь

Достаточным считается значение r_yx ³ |0,700|

При криволинейной форме связи определяем не коэффициент корреляции а теоретическое корреляционное отношение

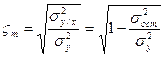где:

s²_у = S(у_i – у_ср)²/n – общая дисперсия отражающая вариацию у под влиянием всех факторов, как известных так и неизвестных.

s²_у/х = S(у_i – у_ср)²/n – дисперсия факторного признака, отражающая вариацию у под влиянием выбранного фактора х.

s²_ост = S(у_i – у_ср)²/n – остаточная дисперсия отражающая вариацию у под влиянием всех остальных факторов (кроме выбранного фактора х)

s²_у = s²_у/х + s²_ост

z_т – изменятся от 0 до ± 1; z_т ³ |0,700|

0 – связи нет

+(-)1 – прямая (обратная) связь

Для множественной корреляции есть специальные (довольно громоздкие) формулы которые даны в литературе по общей теории статистики.