2014-02-24
337
В работе [1] приведены аналитические решения для расчета относительных термических напряжений в любой точке неограниченной пластины при ее конвективном нагреве в печи с постоянной температурой греющей среды 
.
Целью данного раздела является создание объединенного уравнения для аналитического определения указанных величин для тел простой геометрической формы.
Поэтому задачу определения термических напряжений в телах простой формы будем решать в предположении такой же их зависимости от температур на поверхности, в центре и среднемассовой как для плоских тел.
Для цилиндрических тел согласно [8] будут справедливы уравнения (1)...(7), (9), (10) для пластины с заменой координатной функции 
, входящей в уравнение (4) 
, где 
.
Следует отметить, что простому объединению «поддаются» не все величины. Так, амплитуды 
и 
легко обобщаются формулами
(4.159)
а для амплитуды
, (4.160)
где 
;
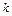— коэффициент геометрической формы, равный 1 — для пластины, 2 — цилиндра и 3 — шара; 
; 
.
Дифференцируя уравнения (2), (3) и (6) по времени, приравнивая производную нулю и используя два члена суммы ряда, получим формулы для расчёта максимальных времен Фурье:
|
|
|
, (4.161)
где 
; 
; 
; 
; 
.
Подставляя 
из (18) в уравнения (2), (6) и (3), получим максимальные значения величин с учётом двух членов ряда:
(4.162)
При 
, 
имеем время 
и максимальное термическое напряжение на поверхности 
; при 
, 
и 
и при 
, 
и 
.
