В работе [3] приведена общая приближенная формула расчета первого корня для тел простой формы
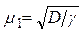 , (4.163)
, (4.163)
где 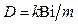 ;
; 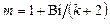 —коэффициент
—коэффициент
термической массивности; 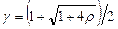 ;
; 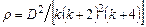 ;
; 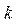 — см. уравнение (4.160); при малых r число
— см. уравнение (4.160); при малых r число 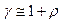 .
.
Для определения приближенных значений остальных корней следует различать два характерных случая нагрева при больших и малых числах Био [4, 5, 6].
При малых числах Био (Bi < 3)
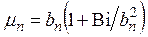 , (4.164)
, (4.164)
где 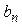 — корни уравнений (8), (14), (15) при
— корни уравнений (8), (14), (15) при 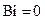 .
.
При больших числах Био (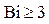 )
)
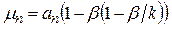 , (4.165)
, (4.165)
где 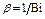 ;
; 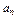 — корни уравнений (8), (14), (15), при
— корни уравнений (8), (14), (15), при 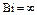 .
.
Следует отметить, что при числах Био 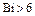 первый корень
первый корень 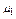 следует вычислять не по уравнению (4.163), а по (4.165).
следует вычислять не по уравнению (4.163), а по (4.165).
Получим упрощенные расчетные соотношения в двух предельных случаях.
Асимптотика при малых числах Био. Первый корень характеристического уравнения вычисляем по соотношению (4.163), а второй — по (4.164). Тогда отношение собственных чисел
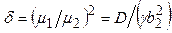 . (4.166)
. (4.166)
Разность квадратов корней 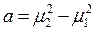
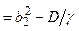 .
.
Первая амплитуда, входящая в характеристическое уравнение температуры поверхности
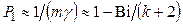 . (4.167)
. (4.167)
По аналогии любая амплитуда
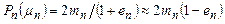 , (4.168)
, (4.168)
где 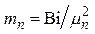 — n -ый коэффициент термической массивности;
— n -ый коэффициент термической массивности; 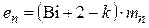 .
.
Интересно отметить, что в отличие от других амплитуд зависимость 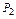 от числа Био носит немонотонный характер, возрастает от нуля до максимального значения
от числа Био носит немонотонный характер, возрастает от нуля до максимального значения 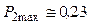 при числе
при числе 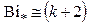 , а затем уменьшается до нуля, оставаясь меньше
, а затем уменьшается до нуля, оставаясь меньше 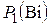 .
.
Введем отношение поверхностных амплитуд
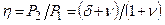 , (4.169)
, (4.169)
где 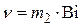 .
.
При определении тепловой амплитуды 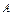 воспользуемся разложением функций
воспользуемся разложением функций 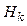 уравнения (4.160) при малых аргументах и обобщая эти разложения, получим
уравнения (4.160) при малых аргументах и обобщая эти разложения, получим
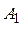
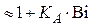 , (4.170)
, (4.170)
где 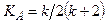 .
.
Для среднемассовой температуры:
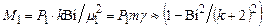 и
и
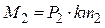 . (4.171)
. (4.171)
Для перепада температур по характеристическому уравнению
 . (4.172)
. (4.172)
Для термических напряжений в центре тела
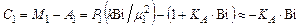 . (4.173)
. (4.173)
Для термонапряжений на поверхности
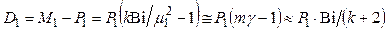 ,
,
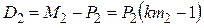 . (4.174)
. (4.174)
С целью проверки амплитуды 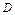 можно использовать равенство
можно использовать равенство 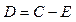 .
.
Выражения для расчета максимальных времен по уравнению (4.161) также упростятся.
Коэффициент поверхности 
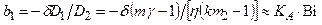 ,
,
для перепада температур 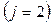
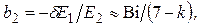 (4.175)
(4.175)
и центра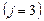
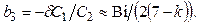
Для оценки различия наиболее возможных максимальных времен, которые получаются в предельном случае при числах 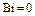 , с помощью уравнений (4.174) составим их разности
, с помощью уравнений (4.174) составим их разности
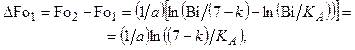 (4.176)
(4.176)
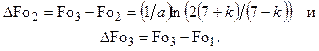 (4.177)
(4.177)
Результаты расчетов разности чисел Фурье по уравнениям (4.175) и (4.176) при 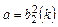 и различном коэффициенте геометрической формы
и различном коэффициенте геометрической формы 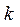 приведены в табл. 1.
приведены в табл. 1.
Таблица 4.3. Разности максимальных времен в зависимости от 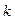 при
при 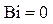
Фактор формы 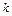
| 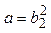
| 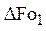
| 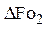
| 
|
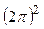
| 0,5703 | 0,1846 | 0,7548 | |
| 3,83172 | 0,2040 | 0,0872 | 0,2912 | |
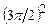
| 0,1166 | 0,0725 | 0,1891 |
Из анализа данных табл. 1 следует, что с ростом коэффициента 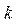 , т. е. при переходе от плоских тел к сферическим, разности
, т. е. при переходе от плоских тел к сферическим, разности  уменьшаются примерно в 3—1,5 раза. Во столько же раз
уменьшаются примерно в 3—1,5 раза. Во столько же раз 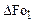 больше чем
больше чем 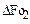 .
.
Для выяснения динамики изменения термических напряжений от фактора формы и других числах Био поступим следующим образом.
Результаты расчетов при 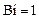 максимальных времен
максимальных времен 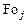 по формуле (4.161) и соответствующих этим временам максимальных термических напряжений на поверхности
по формуле (4.161) и соответствующих этим временам максимальных термических напряжений на поверхности 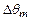 и термонапряжений в центре цилиндра по уравнению (4.162) приведены в табл. 4.4. Там же представлены данные при
и термонапряжений в центре цилиндра по уравнению (4.162) приведены в табл. 4.4. Там же представлены данные при 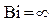 .
.
Таблица 4.4. Коэффициенты 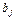 , максимальные времена
, максимальные времена 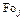 ,
, 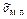 ,
, 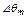 и
и 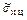 при
при 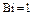 и
и 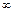
Пластина 
| |||||||
| j | Число Био 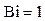
| 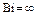
| |||||

| 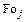
| 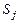
| 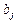
| 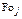
| 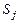
| ||
| 0,121350 | 0,191828 | 0,208348 | |||||
| 0,082567 | 0,226851 | –0,308331 | 1/3 | 0,05666 | –0,98655 | ||
| 0,051086 | 0,270518 | –0,101940 | 0,09993 | 0,11669 | –0,30838 | ||
Цилиндр 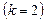
| |||||||
| 0,197757 | 0,107580 | 0,159022 | |||||
| 0,101231 | 0,152028 | –0,306990 | 0,28556 | 0,05074 | –0,96792 | ||
| 0,069533 | 0,176960 | –0,152620 | 0,14446 | 0,07833 | –0,46734 | ||
Шар 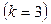
| |||||||
| 0,249570 | 0,070318 | 0,13075 | |||||
| 0,099923 | 0,116690 | –0,30837 | 1/4 | 0,04682 | –0,9449 | ||
| 0,073222 | 0,132440 | –0,18445 | 0,16172 | 0,06153 | –0,5688 | ||
Анализ уравнений (4.161) и табл. 4.4 позволяет сделать вывод о том, что максимум величин наступает в последовательности 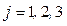 и с ростом числа Био эти времена уменьшаются, а различия максимальных времен увеличиваются, вплоть до
и с ростом числа Био эти времена уменьшаются, а различия максимальных времен увеличиваются, вплоть до 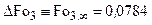 — см. табл. 4.4 для цилиндра.
— см. табл. 4.4 для цилиндра.
На практике технологов интересует вопрос — насколько термические напряжения на поверхности тела больше, чем в его середине. Обозначим их отношение 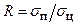 . Наиболее просто
. Наиболее просто 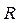 можно найти в стадии регулярного режима нагрева (РРН), который наступает при числах Фурье
можно найти в стадии регулярного режима нагрева (РРН), который наступает при числах Фурье 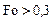 и когда вместо бесконечных сумм в характеристических уравнениях можно ограничиться одним членом ряда. Тогда, деля эти уравнения и учитывая упрощенные соотношения (4.173) и (4.174), получим
и когда вместо бесконечных сумм в характеристических уравнениях можно ограничиться одним членом ряда. Тогда, деля эти уравнения и учитывая упрощенные соотношения (4.173) и (4.174), получим
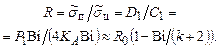 (4.178)
(4.178)
При числе 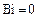
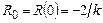 .
.
Таким образом, в отличие от процесса нагрева плоских тел, когда при 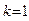
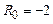 , термические напряжения на поверхности тела в 2 раза больше термонапряжений в центре, при нагреве цилиндрических тел напряжения в центральных точках тела примерно равны или чуть больше, чем на поверхности.
, термические напряжения на поверхности тела в 2 раза больше термонапряжений в центре, при нагреве цилиндрических тел напряжения в центральных точках тела примерно равны или чуть больше, чем на поверхности.
Отношение термонапряжений при 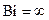
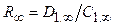 .
.
Следует отметить, что если приближенно считать 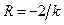 , то из характеристического уравнения будем иметь
, то из характеристического уравнения будем иметь
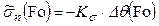 , (4.179)
, (4.179)
где 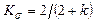 .
.
Это соотношение при 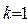 и 2 полностью совпадает с формулами Н.Ю. Тайца [2] для максимальных термических напряжений
и 2 полностью совпадает с формулами Н.Ю. Тайца [2] для максимальных термических напряжений
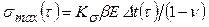 . (4.180)
. (4.180)
 2014-02-24
2014-02-24 656
656








