Случайные величины и функции распределения

Как ранее указывалось, показатели надёжности отражают собой появление различного рода отказов, проявляющихся случайным образом и с различной вероятностью. До сих пор мы оперировали с достоверными (вероятными) и недостоверными (невероятными) событиями. Но в общем случае событие (величина) может обладать произвольной вероятностью. Пусть, например, расчётная частота собственных колебаний турбинной лопатки равна 300 Гци определен разброс частот ± 4%. При этом случайные события - частоты конкретных лопаток могут различным образом распределяться внутри указанного диапазона.

Соотношение между возможными значениями случайной величины и соответствующими им вероятностями появленияназывается законом распределения случайной величины.

Законы распределения могут характеризовать как дискретные так и непрерывные случайные величины. Для дискретной случайной величины (пример с лопаткой) закон распределения может быть представлен рядом, например, в виде таблицы (табл. 3.1). В большинстве практических случаев проще оперировать с распределениями непрерывных случайных величин.

Таблица 3.1 Случайные величины и соответствующие вероятности.

xi	x1	x2	x3	…	xn
Pi	P1	P2	P3	…	Pn

Так как непрерывная случайная величина имеет бесчисленное множество значений, невозможно использовать таблицу дляих представления. Отметим также, что каждое отдельное значение непрерывной случайной величины имеет нулевую вероятность, но можно говорить о вероятности некоторого диапазона возможных значений случайной величины X. Особенностью указанной вероятности непрерывной величины оказывается то, что оценивается не вероятность события X=х (она нулевая), а вероятность события Х<х, где х - произвольная текущая переменная. Вероятность указанного события (Х<х)будет функцией от х, которая обозначается F(x) и называется функцией распределения случайной величины X. При этом

F(x)=P(X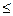x) (3.24)

Часто (3.24) называют интегральной функцией распределения.

Функция F(x) возрастающая, причем F(-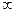)=0 и F(+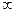)=1. В отдельных точках могут быть разрывы. Возможный вид функции F(x) показан на рис.3.4.

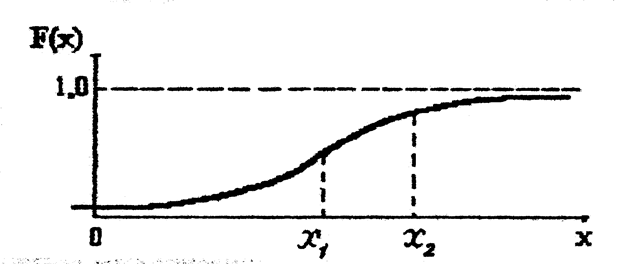
Рис.3.4 Вид функции распределения F(x) непрерывной случайной величины.

Если необходимо найти вероятность появления случайных величин для их некоторого интервала от значения x₁ до значения х₂, то в этом случае вероятность равна

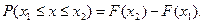(3.25)

При анализе вероятностей также широко используется понятие плотности распределения - первой производной функции распределения случайной величины

f(x)=F'(x), (3.26)

которая изображена на рис 3.5.

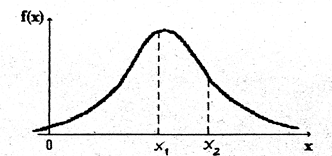
Рис.3.5. Вид плотности функции распределения непрерывной случайной величины.

Для непрерывной функции распределения и плотность распределения непрерывна и положительна. Взаимосвязь между функцией и плотностью распределения

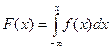(3.27)

Отметим, что функция распределения безразмерна, а размерность плотности распределения соответствует 1/х, то есть обратна размерности самой случайной величины.

Выражение, эквивалентное (3.27), для вероятности случайной величины х, находящейся в диапазоне от значения х₁ до х₂, будет иметь следующий вид

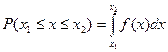(3.28)

Функции F(x) и f(х) удобны для математического описания и решения практических задач оценки различных случайных величин, например, нагрузок, напряжений и так далее. Но их возможно использовать и для характеристики распределения дискретных случайных величин. Рассмотрим результаты испытаний на разрыв п одинаковых стальных образцов. При этом фиксируются число образцов т, разрушившихся при соответствующих уровнях напряжения σ. Плотность распределения для каждого диапазона Δσ будет

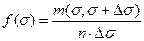, (3.29)

что иллюстрируется ступенчатой функцией на рис.3.6, которую называют гистограммой. Ординаты гистограммы соответствуют среднему числу разрушений (отказов) образцов для диапазона напряжений σ, σ+Δσ. Для получения плотности функции распределения используется огибающая.

В зависимости от реальных процессов распределения случайных величин функции F(x) и f(x) могут иметь, различные произвольные формы и их описание аналогичными функциями распределениячасто затруднено. Для характеристики формы распределений по аналогии с моментами инерции фигур различной формы в теории вероятностей используются моменты. При этом различаются

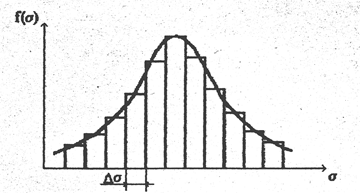
Рис.3.6. Гистограмма и огибающая функция.

начальные и центральные моменты, а также их порядок. В общем виде начальный момент порядка s для дискретной случайной величины х представляется в виде суммы

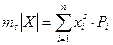, (3.30)

а для случая непрерывной случайной величины

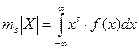. (3.31)

В практических расчетах обычно используют моменты первого и второго порядка. Для случайной величины момент первого и второго порядка называется математическим ожиданием и обозначается М.

Для дискретной случайной величины

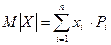. (3.32)

Понятие математического ожидания на примере дискретных случайных величинможно пояснить так. Пусть мы имеем большое число опытов N определения случайной величины X (например, длительной прочности). Обозначим m_i - число раз появления некоторого значения x_i. Тогда отношение m_i/N -можно полагать вероятностью появления x_i, а сумма

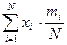. (3.33)

равна математическому ожиданию (см. (3.32)). Но, с другой стороны, (3.33) есть не что иное, как среднее арифметическое всех значений случайной величины X. Отношение m_i/N - частота или статистическая вероятность событий Х=x_i |. Следовательно, математическое ожидание соответствует среднему арифметичес­кому наблюдавшихся случайных величин и это тем более точно, чем больше число опытов.

Математическое ожидание в случае непрерывной случайной величины

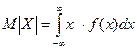. (3.34)

Для характеристики распределений используются также понятия моды и медианы. Мода распределения случайной величины - это наиболее вероятное её значение. Для дискретной случайной величины - это максимальное значение х_i/N, а для непрерывной - значение x_m, при котором плотность вероятности f(x) максимальна (см. рис.3.7.).

Медиана распределения случайной величины - это такое значение х _ме которому соответствует равенство

P(X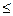x_ме)=P(X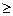x_ме). (3.35)

Медианное значение случайной величины разделяет площадь под графиком функции плотности распределения на две равновеликие части (см.рис.3.7), то есть

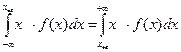. (3.3)

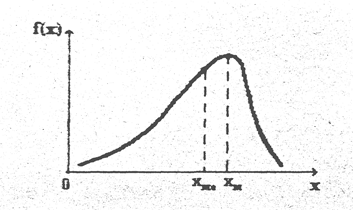
Рис.3.7. Схема определения моды и медианы непрерывной случайной величины.

Для дискретных случайных величин при указанных ранее условиях х _ме будет определено из равенства

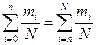. (3.36)

Если кривая f(х) симметрична, то математическое ожидание, мода и медиана совпадают.

Обычно различают начальные и центральные моменты. Введём понятие центрированной случайной величины Х₀, которая связана со случайной величиной X соотношением

Х₀=Х-М, (3.38)

где М - математическое ожидание. Центрирование случайной величины соответствует переносу начала координат в точку, где значение случайной величины равно математическому ожиданию. Моменты, вычисленные по центрированным случайным величинам, называются центральными. Их использование существенно облегчает расчёты вероятностей. Из определения первого центрального момента следует

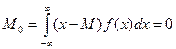. (3.39)

Поэтому математическое ожидание для распределения центрированной случайной величины всегда равно нулю. Важное практическое применение имеет второй центральный момент, который называют дисперсией случайной величины и

обозначают D[X].

Дисперсия случайной величины определяет разброс значений величины около значения её математического ожидания. Для дискретных случайных величин дисперсия или вариация вычисляется как

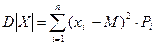(3.40)

В случае непрерывных величин

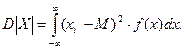(3.41)

На практике вместо дисперсии применяют другую величину – среднее квадратичное отклонение

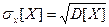, (3.42)

Которое также называют стандартным распределением случайной величины. Удобство в том, что величина σ_х[X] имеет размерность случайной величины и упрощает различные сравнения. Относительной мерой разброса по отношению к среднему значению служит коэффициент вариации

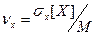(3.43)

Понимание введенных характеристик облегчается, если отметить некоторые аналогии с известными величинами механики. При этом моменты распределения вероятностей соответствуют моментам площадей под кривой плотности распределения. Центральные моменты аналогичны моментам площадей относительно центра тяжести. Математическое ожидание, или среднее значение, - центр тяжести, вариация соответствует моменту инерции, а стандартное отклонение – радиусу инерции этой площади.

3. Законы распределения случайных величин.

В (3.7) отменено, что в задачах надёжности случайные величины, отражающие долговечность и безотказность будут полностью охарактеризованы с вероятностной стороны, если задан как закон распределения, как случайной величины так и распределение ее вероятностей. В зависимости от физических процессов для случайных величин могут иметь место различные вероятности или их распределения. В теории надёжности обычно рассматриваются как дискретные, так и непрерывно распределенные распределения.

3.1. Дискретные распределения

К дискретным распределениям относятся:

• Экспериментальные распределения,

• Биномиальное распределение,

• Распределение Пуассона.

Будем обозначать случайную величину через X, а её возможные значения - х. Тогда вероятность принятия величиной X значений х₁, х₂, …, х_n будет

Р(Х=х₁)=Р₁, Р(Х=х₂)=Р₂, …, Р(Х=х_n)=Р_n, (4.1)

что может быть представлено таблицей (см. табл. 3.1)

Если события несовместны и образуют полную группу событий, то сумма их вероятностей равняется единице

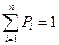. (4. 2)

Рассмотрим более подробно биномиальное распределение, которое может быть использовано дляоценки числа бракованных экземпляров деталей в выборках из неограниченной партий изделий.

Биномиальное распределение основано на применении биномиального коэффициента 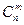и характеризует появление m числа событий в п независимых испытаниях, в каждом из которых вероятность появления события постоянна и равна р. В свою очередь, понятие- биномиального коэффициента основано на понятиях размещений (перестановок) и сочетаний.

Перестановка - есть упорядоченная выборка элементов из некоторого множества S.

Сочетание - есть неупорядоченная выборка элементов из некоторого множества S.

Размещениями из п элементов по m называются такие соединения, которые различаются или самими элементами или их порядком. При этом могут допускаться и не допускаться повторения. Например, выбирая два из трех элементов а, b, с, получим девять размещений с повторениями

1) аа, ab, ас, ba, bb, bс, са, cb, сс,

и шесть размещений без повторений

2) ab, ас, ba, bс, са, cb.

Число перестановок без повторений из и элементов по п (в примере - из трех элементов по два) обозначаются 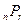и вычисляются по формуле

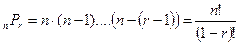(4.3)

Это легко доказывается. Пусть мы имеем множество п элементов (a₁, а₂, …, а _п). В перестановке у нас будут r элементов (a₁, а₂, …, а _r). В качестве a₁ мы можем взять любой из n элементов, в качестве a₂ - любой из оставшихся n-1 элементов. Пусть мы уже выбрали перестановку из i элементов (a₁, а₂, …, а _i), тогда в качестве а_i+n мы можем взять любой из оставшихся n-i элементов. Следовательно мы переходим к выражению (4.3).

Сочетаниями из п элементов по m называются такие

соединения, которые различаются только самими элементами.

Например из трех элементов а,b,с, размещая их по два, можно выделить шесть сочетаний с повторениями

3). аа, bb, сс, ab, ас, bс,

и три сочетания без повторений

4). ab, ac, bc.

Все указанные варианты наглядно иллюстрируются таблицей на рис 4.1.

1) 3)		a	b	c	2) 4)		a	b	c
a	aa	ab	ac	a		ab	ac
b	ba	bb	bc	b	ba		bc
c	ca	cb	cc	c	ca	cb
	a	b	c		a	b	c
a	aa	ab	ac	a		ab	ac
b		bb	bc	b			bc
c			cc	c

Рис. 4.1. Таблица возможных перестановок и сочетаний.

Сочетание без повторений из n элементов по r, например a₁, а₂, …, а _r приводит к r! различным перестановкам, т.е. по всем r! перестановкам элементов a₁, а₂, …, а _r. Следовательно, число сочетаний из n элементов по r, которое обозначается _nС_r определяется как

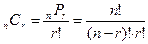, (4.4)

и называется биномиальным коэффициентом.

Биномиальное распределение основано на использовании сочетаний без повторений, получаемом при испытаниях Бернулли. Предположим, что некоторой ситуации имеется n возможных взаимно исключающих исходов. Эти возможные исходы будем для определенности называть удачными и неудачными. Предположим, что вероятность удачного события в каждом отдельном испытании известна и равна р. Очевидно, что вероятность неудачного исхода q = 1-р.

Если выполняется n независимых испытаний Бернулли и справедливо биномиальное распределение, то испытание считается независимым, если исход испытания не зависит от исходов предыдущих испытании.