Addition Real Nambers
Сложение вещественных чисел
Определим сложение и умножение числовых множеств полагая,
C + U ={ z |$x ÎC $y ÎU z = x+ y }=:{x +y|x ÎC Ù y ÎU },
C×U ={ z |$x ÎC $y ÎU z =xy}=:{xy |x ÎC Ù y ÎU }
Эти определения годятся для любых чисел, хотя пока их можно было бы применять лишь к числам рациональным, для которых сумма и произведение уже определены.
Сложение и умножение числовых множеств коммутативны и ассоциативны, обладают нулем - множеством, состоящим из одного нуля {0}, и единицей – множеством, состоящим из одной единицы {1}, связаны между собой дистрибутивным законом, но, в общем, когда числовое множество не состоит из одного единственного элемента, у него нет противоположного и обратного
C + U = U + C, C × U = U × C;
(C + U)+ Z = C +(U + Z)=: C +U+ Z, (C × U) Z = C ×(U×Z)= CUZ;
C +{0}= C; C ×{1}=C
Определим также множество - C из противоположных элементов множества Х:
- C ={| x |- xÎC},
|
|
 |
а также множество C -1 из обратных элементов множества C, если оно не содержит нуля:
C -1={ x | x -1 ÎC }, если 0 Ï 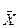 Û0 ÏC 1
Û0 ÏC 1
Если непустое множество Х, не являетсяодноэлементным множеством, то его сумма с множеством -C из его противоположных элементов тоже не является одноэлементным множеством; она содержит 0 и вместе со всяким числом содержит противоположное ему число; на числовой прямой эти множества симметричны относительно начала координат:
C +(- C)º C - C ={ x - y | x,y ÎC },
0ÎC- C, аÎ CÛ- аÎC - C;
{ а }+(-{ а })º{ а }-{ а }º{ а }+{- а }={0}.
Если непустое множество Х, не содержащее нуля, не является одноэлементным, то его произведение на множество Х-1из его обратных элементов тоже не является одноэлементным множеством; оно содержит 1 и вместе со всяким числом содержит обратное ему число.
Х × C -1@C/ C ={ x /y| x, yÎC }, 0 ÏC Û0 Ï C -1;
1 ÎC × C -1, аÎC × C -1Û а -1 ÎC × C -1; C(U + Z)= CU + CZ
{ а }×{ а }-1º{ а }/{ а }º{ а }×{ a -1}={1}
C +={ x | xÎC и x >0}-множество положительных чисел из множества Х – положительная часть множества Х.
Х -={ x | xÎC Ù x <0}множество отрицательных чисел из множества Х -отрицательная часть множества Х.
(~ C)±=- C ±, 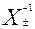 =(Х -1)±
=(Х -1)± C \{0}= C +È C -
C \{0}= C +È C -
C -1= Х 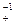 È C
È C 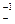 , (CC -1)+ = C + C
, (CC -1)+ = C + C 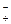 È C -× C
È C -× C 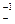 , (CC -1)-= C + × C
, (CC -1)-= C + × C 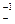 È C -× C
È C -× C 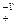
На числовой прямой множества точек Х и Х -1 связаны друг с другом инверсией относительно нульмерной единичной сферы | x |=1, представляющий собой двухточечное множество {-1,+1} C+ и C 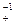 =(C -1)+ связаны инверсией относительно точки 1, а C
=(C -1)+ связаны инверсией относительно точки 1, а C 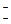 и C
и C 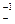 =
= 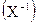 - инверсией относительно точки –1. Точки связанные инверсиейотносительно нульмерной единичной сферы | х |=1 а) одного знака и б) произведение их расстояний до начала координат (модулей) равно 1.
- инверсией относительно точки –1. Точки связанные инверсиейотносительно нульмерной единичной сферы | х |=1 а) одного знака и б) произведение их расстояний до начала координат (модулей) равно 1.
Сложение вещественных чисел. Суммой вещественных чисел – сечений a = A | A ¢ и b = B | B ¢ называется вещественное число – сечение g = C | C ¢, внутренность конечного (верхнего) класса
которого есть, по определению сумма внутренностей нижних (верхних) классов слагаемых:
a + b = g Û 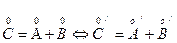
Другими словами сумма вещественных чисел – это вещественное число, которое заключено между всевозможными суммами рациональных чисел из внутренностей нижних классов слагаемых и всевозможных суммами чисел из внутренностей верхних классов слагаемых:
" аÎ 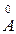 , bÎ
, bÎ 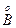 , а ¢ Î
, а ¢ Î 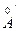 , b ¢ Î
, b ¢ Î 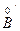 а +b<y< a ¢+ b ¢
а +b<y< a ¢+ b ¢
Корректность этого определения следует из следующих утверждений.
Множество 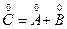 действительно может рассматриваться как внутренность нижнего класса некоторого сечения; одновременно множество
действительно может рассматриваться как внутренность нижнего класса некоторого сечения; одновременно множество 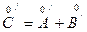 является внутренностью верхнего класса того же сечения. Сумма вещественных чисел определена данным определением для любых двух вещественных чисел и однозначно, т.е. не может быть разных вещественных чисел удовлетворяющих определению суммы для фиксированных слагаемых.
является внутренностью верхнего класса того же сечения. Сумма вещественных чисел определена данным определением для любых двух вещественных чисел и однозначно, т.е. не может быть разных вещественных чисел удовлетворяющих определению суммы для фиксированных слагаемых.
3Действительно,  вместе с любым числом а + b, aÎ
вместе с любым числом а + b, aÎ  , bÎ
, bÎ  содержит все меньшие: а + b > r Þ а + b - r >0Þ а -(a + b - r)< а, т. е. а -(а +b-r) Î
содержит все меньшие: а + b > r Þ а + b - r >0Þ а -(a + b - r)< а, т. е. а -(а +b-r) Î  ; после прибавления к обеим частям последнего неравенства числа bÎ B имеем r = а -(а+b - r)+ b < a +b.
; после прибавления к обеим частям последнего неравенства числа bÎ B имеем r = а -(а+b - r)+ b < a +b.
В  нет наибольшего числа, поскольку наибольших чисел нет по определению в
нет наибольшего числа, поскольку наибольших чисел нет по определению в  и
и  . Поэтому для аÎ
. Поэтому для аÎ  и bÎ
и bÎ  найдутся большие из тех же классов а < а 1, а 2 Î
найдутся большие из тех же классов а < а 1, а 2 Î  ; b < b 2; b 2 Î
; b < b 2; b 2 Î  .Поэтому для всякого числа а + b из
.Поэтому для всякого числа а + b из  +
+ в этом множестве есть большее число а 2+ b 1.
в этом множестве есть большее число а 2+ b 1.
Аналогичные рассуждения показывают, что  ¢ можно рассматривать как верхний класс некоторого сечения.
¢ можно рассматривать как верхний класс некоторого сечения.
Любое число из  меньше любого числа из
меньше любого числа из  ¢. Действительно, если а + bÎ
¢. Действительно, если а + bÎ  a ¢+b¢Î
a ¢+b¢Î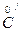 где АÎ
где АÎ  , b Î
, b Î  , а ¢ Î
, а ¢ Î  ¢, b¢Î
¢, b¢Î  ¢ и, следовательно, а < а ¢ и b < b ¢, то складывая последние неравенства получаем требуемое, а + b < а ¢+ b¢.
¢ и, следовательно, а < а ¢ и b < b ¢, то складывая последние неравенства получаем требуемое, а + b < а ¢+ b¢.
В  и
и  ¢ можно найти числа, разность которых меньше любого наперед заданного положительного e>0. По третьей теореме об аппроксимации есть числа а, а; b; b ¢ разность которых меньше e/2: 0< а ¢- а <e/2, 0<b¢-b<e/2, откуда 0< а ¢+ b ¢-(а + b)=(а ¢- а)+(b ¢- b)<
¢ можно найти числа, разность которых меньше любого наперед заданного положительного e>0. По третьей теореме об аппроксимации есть числа а, а; b; b ¢ разность которых меньше e/2: 0< а ¢- а <e/2, 0<b¢-b<e/2, откуда 0< а ¢+ b ¢-(а + b)=(а ¢- а)+(b ¢- b)<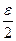 × Поэтому множество Q \(
× Поэтому множество Q \(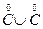 ¢¢) содержит не более одного элемента (числа), согласно второй теореме об аппроксимации. Если указанное множество пустое (=Æ), то
¢¢) содержит не более одного элемента (числа), согласно второй теореме об аппроксимации. Если указанное множество пустое (=Æ), то  =С,
=С,  ¢=C¢, C | C ¢= g -однозначно определенная сумма. Если Q \(
¢=C¢, C | C ¢= g -однозначно определенная сумма. Если Q \(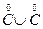 ¢)={ c },где сÎ Q, то с = max (
¢)={ c },где сÎ Q, то с = max (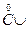 {c}=min(
{c}=min( ¢È{c} так что (
¢È{c} так что (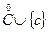 |
| ¢=
¢= |(
|( ¢È{c})-сечение производимое числом с. Подчеркнем, что наличие такого с не означает, что числа-слагаемые a и b рациональны8
¢È{c})-сечение производимое числом с. Подчеркнем, что наличие такого с не означает, что числа-слагаемые a и b рациональны8
Данное определение суммы вещественных чисел сохраняет сумму рациональных чисел неизменной. Точнее, сумма а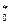 +
+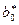 сечений b
сечений b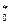 и b
и b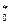 производимых рациональными числами а 0 и b0 есть сечение (а 0 +b0)* производимое их суммой:
производимых рациональными числами а 0 и b0 есть сечение (а 0 +b0)* производимое их суммой:
а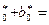 (а 0+b0)*
(а 0+b0)*
3" aÎ  , bÎ
, bÎ  , а ¢ Î
, а ¢ Î  ¢, b ¢Î
¢, b ¢Î ¢ а < а 0< а ¢Ùb<b0< b ¢Þ a + b < a 0+ b 0< a ¢+b¢. Поэтому а 0+ b 0 удовлетворяет условием налагаемым на сумму и так как последняя определена
¢ а < а 0< а ¢Ùb<b0< b ¢Þ a + b < a 0+ b 0< a ¢+b¢. Поэтому а 0+ b 0 удовлетворяет условием налагаемым на сумму и так как последняя определена однозначно, то она совпадает с сечением (а 0+ b 0)*8
однозначно, то она совпадает с сечением (а 0+ b 0)*8
В терминах сечений естественно получать лишь те свойства суммы, которые достаточны для аксиоматического построения теории вещественных чисел: ассоциативность, коммутативность, существование нуля, существование противоположного, свойства неравенств (порядка) относительно сложения.
1.Коммутативность: a + b = b + a -независимость суммы от порядка слагаемых.
2.Ассоциативность: a(b+g)=(a+b)+g-независимость суммы от порядка выполнения действий (расстановки скобок).
3.Существование нуля: сечение 0* производимое 0 обладает свойством 0*+a= a: прибавление нуля к любому числу не меняет его.
4.Существование противоположного: для любого числа a = A | A ¢ его сумма с противоположным - a:=(- A ¢)|(- A) равна нулю (- a)+ a =0*.
5.Неравенство между вещественными числами сохраняется при прибавлении к обеим его частям одного и того же числа: a < b Þ a + g < b + g.
3 +
+ =
= +
+ , из-за коммутативности сложения рациональных чисел.
, из-за коммутативности сложения рациональных чисел.
 +
+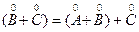 из-за ассоциативности сложения рациональных чисел.
из-за ассоциативности сложения рациональных чисел.
0*= Q -|(Q +È{0})=(Q -È{0}| Q *. Для а = А | A ¢ имеем Q -+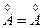 Q ++
Q ++ ¢=
¢=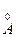 ¢.
¢.
Действительно, в  * нет наибольшего. Всякий элемент из Q +
* нет наибольшего. Всякий элемент из Q + меньше некоторого элемента из
меньше некоторого элемента из 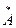 как сумма с отрицательным числом. Поэтому Q -+
как сумма с отрицательным числом. Поэтому Q -+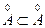 . Для всякого элемента из
. Для всякого элемента из  найдется равный ему элемент из Q -+
найдется равный ему элемент из Q -+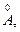 точка числа Q -+
точка числа Q -+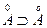 и, следовательно, Q -+
и, следовательно, Q -+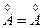 . В самом деле, если аÎ
. В самом деле, если аÎ 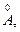 то можно указать а 1 Î
то можно указать а 1 Î  большее а: а < а 1. Но так как а = а 1+(а - а 1), где а 1Î
большее а: а < а 1. Но так как а = а 1+(а - а 1), где а 1Î , а а - а 2<0, т.е. а - а 2 Î Q -,то аÎ Q -+
, а а - а 2<0, т.е. а - а 2 Î Q -,то аÎ Q -+ .
.
Для произвольного сечения a = A | A ¢ множества (- А) и (- А ¢) из противоположных элементов для классов А и А ¢, непусты (ибо таковы сами А и А ¢), не пересекаются (по той же причине с учетом того что (- а)=(- а ¢) Û а = а ¢), их объединение есть Q (так как A È A ¢= Q,то "r Î Q либо - rÎA, т.е. -r= а или g =-a а значит gÎ - A либо - rÎA ¢ и следовательно rÎ(- A ¢)), наконец, для rÎ( - A) и g ¢ Î (- A ¢) имеем (- r) ÎA и следовательно (- r)<(- r ¢) т.е. r > r ¢. (- )+
)+ ¢= Q +,
¢= Q +, +(-
+(- ¢)= Q - т.е. a +(- a)=0*× Легко понять, что (-
¢)= Q - т.е. a +(- a)=0*× Легко понять, что (- ) – внутренность класса (-А), (- а)+ а ¢>0; для r>0 $a, а
) – внутренность класса (-А), (- а)+ а ¢>0; для r>0 $a, а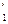 такие что 0< a ¢- a<g. Тогда а 1< a +g=: a ¢, причем a¢ - a º a ¢+(- a)=r - все числа из Q + содержатся в (-
такие что 0< a ¢- a<g. Тогда а 1< a +g=: a ¢, причем a¢ - a º a ¢+(- a)=r - все числа из Q + содержатся в (- )+ A ¢.
)+ A ¢.
a £ b Û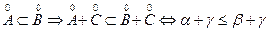 . Сохранение строгого неравенства получается “алгебраически” из того что a=bÛa+g=b+g 8
. Сохранение строгого неравенства получается “алгебраически” из того что a=bÛa+g=b+g 8
 2014-02-24
2014-02-24 589
589








