Произведение вещественных чисел
Добуток дійсних чисел.
Потребуем, чтобы умножение было дистрибутивно по отношению к сложению:
a (b+g ) = a b+ a. g
Отсюда вследствие единственности нуля, доказываемой алгебраически, имеем для любых фиксированных a,b
ab = a (b +0)= ab + a 0 Þ a× 0=0
Произведение любого вещественного числа на 0 равно нулю.
0 = a ×0= a (b +(- b))= ab + a ×(- b)Þ a ×(- b)=-- ab
вследствие единственности противоположного, доказываемой алгебраически.
Произведение числа на противоположное другому числу есть противоположное произведению этих чисел. Отсюда правило знаков: плюс (умноженный) на плюс и минус на минус дают плюс, а плюс на минус и минус на плюс дают минус:
ab º(+ a)(+ b)=(- a)(- b) a (- b)º(+ a)(- b)=(- a)b=(- a)(+ b)=-(ab)
(- a) (- b)=-(a (- b))=-(-(ab))= ab - т.к. противоположное число единственно.
Таким образом, в предположении дистрибутивности достаточно определить произведение положительных чисел, для остальных произведение определится правилом знаков и свойством 0 обращать в нуль произведение.
Для положительных вещественных чисел a, b >0, т.е. для a = A ½ A ¢ и b = B | B ¢ таких, что A ¢ B ¢Ì Q +, назовем произведением ab вещественное число g = C | C ¢ внутренность, верхнего класса которого равна произведению внутренностей верхних классов сомножителей  ¢=
¢= ¢
¢  ¢: для ab >0
¢: для ab >0
ab =gÛ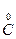 ¢=
¢= ¢
¢  ¢
¢
а положительная часть внутренности нижнего класса равна произведению положительных частей внутренностей нижних классов сомножителей: для a, b >0
 +=
+= +
+ +
+
Другими словами произведение положительных вещественных чисел, это вещественное число, которое заключено между всевозможными произведениями рациональных чисел из положительных частей внутренностей нижних классов сомножителей и всевозможными произведениями чисел из внутренностей верхних классов сомножителей.
"D Î  +, bÎ
+, bÎ  +, а ¢ Î
+, а ¢ Î  ¢, b ¢ Î
¢, b ¢ Î  ¢ аb < g < а ¢ b ¢
¢ аb < g < а ¢ b ¢
Проверка корректности определения  ¢ вместе с любым числом а ¢ b ¢, а ¢ Î
¢ вместе с любым числом а ¢ b ¢, а ¢ Î  ¢, b ¢ Î
¢, b ¢ Î  ¢ содержит все большие: 0 < a ¢ b ¢< r Þ
¢ содержит все большие: 0 < a ¢ b ¢< r Þ
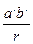 <1 Þ а ¢:(
<1 Þ а ¢:(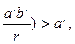 так что левая часть Î
так что левая часть Î  ¢ Поэтому
¢ Поэтому
r =[ a ¢:(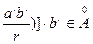 ¢
¢ ¢ Þ
¢ Þ  ¢
¢ ¢ можно рассматривать как внутренность верхнего класса некоторого сечения.
¢ можно рассматривать как внутренность верхнего класса некоторого сечения.
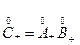 вместе с любым числом аb, где аÎ
вместе с любым числом аb, где аÎ 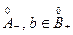 содержит и всякое меньшее положительное число: 0 <r < ab Þ
содержит и всякое меньшее положительное число: 0 <r < ab Þ 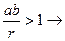 а:(
а:(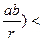 а, так как левая часть Î
а, так как левая часть Î 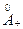 .
.
Поэтому r =[ a:(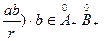 Þ
Þ 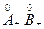 можно рассматривать как внутренность положительной части нижнего класса некоторого сечения.
можно рассматривать как внутренность положительной части нижнего класса некоторого сечения.
B  ¢ нет наименьшего числа в
¢ нет наименьшего числа в 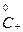 - наибольшего. Так как таковых нет в
- наибольшего. Так как таковых нет в  ¢ и
¢ и  ¢, то для любых а¢, b ¢ есть a ¢, b ¢ есть
¢, то для любых а¢, b ¢ есть a ¢, b ¢ есть 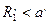 и
и 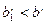 , что после перемножения дает
, что после перемножения дает 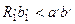 . Для
. Для 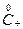 рассуждения аналогично.
рассуждения аналогично.
 Любое число из
Любое число из 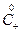 и
и  ¢ меньше любого числа из
¢ меньше любого числа из ¢:0< a < a 0<b<b¢ Þ 0< ab < a ¢b¢.
¢:0< a < a 0<b<b¢ Þ 0< ab < a ¢b¢.
В + и
+ и  ¢ можно найти числа, разность которых меньше любого наперед заданного положительного числа e>0× Можно ограничиться рассмотрением а ¢< а
¢ можно найти числа, разность которых меньше любого наперед заданного положительного числа e>0× Можно ограничиться рассмотрением а ¢< а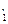 , b ¢<b
, b ¢<b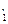 , где а
, где а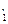 , b
, b  произвольные наперед заданные числа. Если а ¢- a < d и b ¢-b< d, то
произвольные наперед заданные числа. Если а ¢- a < d и b ¢-b< d, то
 a ¢b- ab = a ¢ b ¢- a ¢b+ a ¢ b - a b = a ¢(b ¢-b)+(a ¢- a)b< d (a ¢+b)<d(a ¢+b¢ ¢)< d (a
a ¢b- ab = a ¢ b ¢- a ¢b+ a ¢ b - a b = a ¢(b ¢-b)+(a ¢- a)b< d (a ¢+b)<d(a ¢+b¢ ¢)< d (a  +b1¢)
+b1¢)
Если взять d<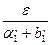 , то получим требуемое. Здесь скажем a ¢< a
, то получим требуемое. Здесь скажем a ¢< a  без ограничения общности, так как во внутренностях верхних классов нет наименьших. Поэтому от а ¢ удовлетворяющего неравенству а ¢- а <8 можно перейти к меньшему если это необходимо, удовлетворяющего кроме этого неравенства также и условию а ¢< a ¢1.
без ограничения общности, так как во внутренностях верхних классов нет наименьших. Поэтому от а ¢ удовлетворяющего неравенству а ¢- а <8 можно перейти к меньшему если это необходимо, удовлетворяющего кроме этого неравенства также и условию а ¢< a ¢1.
Данное определение произведения вещественных чисел сохраняет произведения рациональных чисел неизменными. Точное произведение a 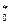 b
b 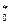 сечений a
сечений a 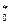 и b
и b 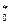 производимых рациональными числами а 0 и b 0 есть сечение (а 0 b 0)* производимое их произведением:
производимых рациональными числами а 0 и b 0 есть сечение (а 0 b 0)* производимое их произведением:
а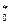 ×b
×b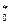 =(a 0b0)*
=(a 0b0)*
30< a < a 0< a ¢ Ù 0< b < b 0< b ¢ Þ 0< ab < a 0 b 0< a ¢b¢× Поэтому a 0b0 удовлетворяет условиям налагаемым на произведение и так как последнее определено однозначно, то оно совпадает с сечением (a 0 b 0)*8
Коммутативность: ab = ba Ü ¢
¢ ¢=
¢= ¢
¢ ¢ так как произведение рациональных чисел коммутативно.
¢ так как произведение рациональных чисел коммутативно.
 Ассоциативность: a (bg)=(ab) g Ü
Ассоциативность: a (bg)=(ab) g Ü  ¢(
¢( ¢
¢ ¢)=(
¢)=(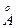 ¢
¢ ¢)
¢) ¢ так как произведение рациональных чисел ассоциативно.
¢ так как произведение рациональных чисел ассоциативно.
 Существование единицы: a ×1= a ×
Существование единицы: a ×1= a ×  ¢
¢ ¢=
¢= ¢, если
¢, если  ¢={ bÎ Q | b >1}-внутренность верхнего класса сечения 1* которое производится рациональным числом 1.
¢={ bÎ Q | b >1}-внутренность верхнего класса сечения 1* которое производится рациональным числом 1.
 Так как в
Так как в  ¢ входят числа >1, то
¢ входят числа >1, то  ¢
¢ ¢Ì
¢Ì ¢. Взяв a
¢. Взяв a 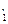 < a
< a 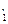 и b ¢=
и b ¢=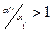 получим a ¢= a
получим a ¢= a 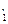 (
(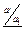 ) Î
) Î  ¢
¢ ¢т.е.
¢т.е.  ¢Ì
¢Ì ¢
¢ ¢.
¢.
 Существование обратного: a -1× a =1, где a = A | A ¢, a -1= B | B ¢ причем для a >0, для a <0 по правилу знаков, 0 не имеет обратного.
Существование обратного: a -1× a =1, где a = A | A ¢, a -1= B | B ¢ причем для a >0, для a <0 по правилу знаков, 0 не имеет обратного. ¢=
¢= ¢
¢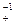
 и
и 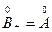 ¢-1.
¢-1.
Действительно a × a -1 заключено между всевозможными произведениями вида аb и а ¢b ¢, в частности между всевозможными числами вида 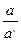 и
и 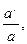 соответствующих выбору b = a ¢-1 и b ¢= a -1.
соответствующих выбору b = a ¢-1 и b ¢= a -1.
Разность таких чисел можно сделать сколь угодно малой, а так как между ними содержится 1: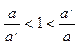 , то это и есть что и требовалось доказать.
, то это и есть что и требовалось доказать.
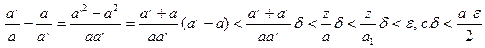 ,
,
где 0< а1 < a; так как в 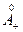 нет наибольшего, то а можно без ограничения общности брать > a 1 увеличение а только уменьшает разность a ¢- a.
нет наибольшего, то а можно без ограничения общности брать > a 1 увеличение а только уменьшает разность a ¢- a.
Неравенства между вещественными числами сохраняется при умножении обеих его частей на одно и то же положительное число
a £ b Ù g >0 Þ ag £ bg ×
 2014-02-24
2014-02-24 562
562








