Полнота ИВ

Теорема о полноте ИВ. Формула ИВ является теоремой ИВ т., и т.т., к. она является тавтологией.

3Необходимость. Всякая теорема ИВ является тавтологией. Легко убедиться прямой проверкой, что все аксиомы ИВ являются тавтологиями в любой из формулировок ИВ. Легко убедиться, пользуясь таблицей истинности для импликации, что правила вывода ИВ, для определенности – МР, в применении к тавтологиям дают тавтологии: 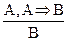если А и АÞВ тождественны истинны, то таковой будет и В.

То же можно сказать и о правиле .

Правило подстановки, если оно используется, тоже сохраняет тавтологию: суперпозиция постоянной функции (значения истинности тавтологии) с любыми функциями дает постоянную функцию с тем же значением. Поэтому теоремы ИВ получающиеся из аксиом ИВ (тавтологий) применением правил вывода (сохраняющих тавтологичность) необходимо являются тавтологиями.

Достаточность. (Kalmar L). Всякая формула ИВ, являющаяся тавтологией, выводима в ИВ.

Лемма. Если некоторая формула выводима из какого-нибудь списка гипотез и выводимость сохраняется после замены одной из гипотез в списке ее отрицанием, то эта формула выводится также из сокращенного на упомянутую гипотезу списка. Это утверждение можно представить в виде правила вывода для секвенций

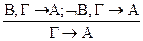
3Теорема дедукции применительно к секвенциям Г,В ® А и Г,ØB ® A дает секвенции G ® BÞA и Г ® Ø BÞA. Если записать сначала последовательность формул – вывод импликации В Þ А из списка гипотез Г, а затем – последовательность формул – вывод импликации Ø BÞА из списка гипотез Г, то нетрудно убедиться, что получится последовательность формул – вывод из списка гипотез Г, среди формул которого встречаются обе импликации ВÞА иØ BÞA. Если среди теорем ИВ встречаются описываемые схемой тавтологий.

(*) (ВÞA)Þ(( Ø BÞA)ÞA)

1 ж 0 0 0 1 1 0 0 0

то добавив к построенному выше выводу из гипотез Г вывод этой схемы тавтологий не привлекающий гипотез, получим ее вывод из гипотез Г в котором встречаются импликации В ÞA и Ø BÞA. Дописав к этому выводу формулы

( Ø BÞA)ÞА [следует из схемы тавтологий (*) и ВÞA по МР]

А [ следует из предыдущей формулы и Ø BÞA

по МР ]

получим вывод формулы А из списка гипотез Г.

Если доказывать более простое утверждение, чем то, которое означает достаточность, а именно: можно указать конечное число тавтологий – схем аксиом обеспечивающее выводимость всех тавтологий, то можно не беспокоиться о выводе формулы (*) приняв ее как аксиому. Ниже мы так и поступаем относя вывод (*) и других схем тавтологий, необходимых для проводимого рассуждения, к громоздковатым и скучноватым, хоть и полезным упражнениям 8.

Лемма. Из гипотез – литералов – составляющих элементарной конъюнкции истинной при заданном наборе значений истинности пропозициональных переменных, выводится всякая формула ИВ построения из всех или только из части этих переменных, истинная для указанного набора истинностных значений, и отрицание всякой такой формулы ложной для этого набора истинностных значений. Иными словами справедлива (истинна) секвенция

(**)

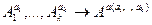
где - пропозициональные переменные из которых или из части которых строится формула А, 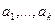– набор истинностных значений этих переменных, 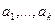– соответствующее истинностное значение формулы А, и по определению

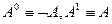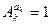т.ч.Û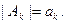

wИндукция по числу связок в формуле А.

Начальный шаг индукции. Если связок нет вообще А = А и требуемое тривиально:

А ^а ® А ^а

– вывод А ^а из гипотезы А ^а состоит из единственной формулы–гипотезы А ^а. Не нарушая выводимость список гипотез можно расширить литералами построенными из других переменных.

Предположение индукции. Для любой формулы А содержащей не более чем n связок истинна секвенция (** ).

Индукция. Рассмотрим формулу А содержащую n+1 связку. Для простоты будем рассматривать формулировку ИВ с основными связками Ø и Þ. Тогда либо а) А =Ø B, либо б) А=(ВÞС), где формулы В и С содержат не более чем n связок.

а) Если а =1, то b =0 и по предположению индукции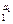A,…,A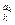 ® Ø B=A.

Если а =0, то b =1 и по предположению индукции 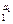A ,¼, A 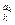® В. Т.к Ø A= ØØ B

добавим к аксиомам схему тавтологий АÞ ØØ A (при использовании конкретного списка аксиом надо было бы доказать, что это схема теорем). Вывод В становится выводом А^а= Ø A добавлением к нему “аксиомы” ВÞ ØØ B и формулы ØØ B=А^а следующей из “аксиомы” и В по МР.

б) А=ВÞС. Если а =1 то возможны b = с =0, b = с =1 и b =0, с =1.

Нужны “аксиомы”

Ø BÞ( Ø СÞ(BÞС))

1 0 0 1 0 0 ж 0 0

ВÞ(СÞ(BÞС))

1 0 1 0 ж 0 0.

Ø BÞ(СÞ(BÞС))

1 0 0 1 0 ж 0 0

Если а =0, то b =1 и с =0. Нужна “аксиома”

ВÞ( Ø СÞ Ø (BÞС)).

1 0 1 0 0 0 1 ж 0 8

Осталось вывести в рассматриваемой формулировке ИВ использованные в рассуждении “аксиомы”. Вывод будет основан на следующем вспомогательном утверждении.

Имеют место секвенции

L1. АÞB,ВÞС ® АÞС;

L2. АÞ(ВÞС),В ® AÞС.

wL1. Докажем секвенцию А, АÞВ, ВÞС ® С из которой согласно теореме дедукции немедленно следует требуемая секвенция. Имеем

1. А [гипотеза]

2. АÞB [гипотеза]

3. В [МР из 1 и 2]

4. ВÞС [гипотеза]

5. C [МР из 3 и 4].

L2. Докажем секвенцию А ,АÞ(BÞС),В ® С из которой согласно теореме дедукции немедленно следует требуемая секвенция. Имеем.

1. А [гипотеза]

2. АÞ(BÞС [гипотеза]

3. ВÞС [МР из 1 и 2]

4. В [гипотеза]

5. С [МР из 4 и 3] 8

Т1. ® ØØ AÞA

w1.(ØAÞ ØØ A)Þ(( Ø AÞ Ø A)ÞA	[ А3 с В® Ø A]
2. ØAÞ Ø A	[принцип тождества с А® Ø A ]
3.(ØAÞ ØØ A)ÞA	[1 и 2 согласно L2]
4.ØØ AÞ( Ø AÞ ØØ A)	[A1 с А® ØØ A,B® Ø A ]
5.ØØ AÞA	[4 и 3 согласно L1] 8

Т2. ® AÞ ØØA

81.(ØØØ AÞØA)Þ(( ØØØ AÞA)Þ ØØ A)	[А3 с А ®ØØ A,B ® A ]
2.ØØØ A ÞØ A	[T1 с А ®Ø A ]
3.(ØØØ AÞA)	[МР из 2 и 1]
4. А Þ(ØØØ AÞA)	А 1 с B®ØØØA]
5 .А ÞØØ A	[4 и 3 согласно L1] 8

Cеквенция А,Г ® А имеет место поскольку вывод А из гипотез А,Г содержит только гипотезу А.

Т3. ® AÞ(BÞ(AÞB) получается из очевидной секвенции А,В,А ® В тройным применением теоремы дедукции.

Т4.. ® Ø AÞ(BÞ( АÞB)) получается из очевидной секвенции Ø A,B,A ® B тройным применением теоремы дедукции.

Т5. ® (Ø AÞ Ø B) Þ(BÞA)

wСтроим вывод секвенции Ø AÞ Ø B, B ® A из которой требуемое получается двойным применением теоремы дедукции.

1.Ø A ÞØ B	[гіпотеза]
2.(Ø AÞ Ø B) Þ((Ø AÞB)Þ A)	[A3]
3.(Ø AÞB)Þ A	[МР из 1 и 2]
4. В Þ(Ø A Þ B)	[А1 с А ®B,B® Ø A ]
5. В	[гипотеза]
6.ØAÞB	[МР из 5 и 4]
7.А	[ МР из 6 и 3] 8

Т6. ® (AÞB)Þ(Ø BÞ Ø A)

wВыводим секвенцию А Þ B ® Ø B ÞØA из которой требуемое получается по теореме дедукции.

1. АÞB	[гипотеза]
2.ØØ A Þ A	[Т1]
3.ØØ A Þ B	[2 и 1 согласно L1]
4. В ÞØØ B	[T2 c A ® B ]
5.ØØ A ÞØØ B	[3 и 4 согласно L1]
6.(ØØ A ÞØØ B) Þ(Ø B ÞØ A)	[Т5 с А ®Ø A,B ®Ø B ]
7.Ø B ÞØ A	[МР из 5 и 6] 8

Т7. ® A Þ(Ø B ÞØ(A Þ B)).

wНачинаем с записи МР в виде секвенции А, АÞB ® B. Дважды применяя теорему дедукции имеем ®AÞ((AÞB)ÞВ). Но ® ((AÞB)ÞB)Þ (Ø B ÞØ(AÞB)) [Т6 с A ® AÞB ]. Согласно L1 отсюда имеем требуемое 8

Т8. ® Ø A Þ(Ø BÞ (AÞB))

w Выводим секвенцию Ø A, Ø B ® A Þ B отсюда требуемое получается двойным применением теоремы дедукции.

1.Ø А	[гипотеза]
2.(Ø B ÞØ A)Þ(А Þ B)	[T5 с А®В, В®A ]
3.Ø B Þ(АÞB)	[2 и 1 согласно L2]
4.Ø B	[гипотеза]
5. АÞВ	[МР из 4 и 3]8