Евклидовы пространства.
Определение. Вещественное линейное пространство 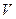 называется евклидовым, если на нем выделена симметричная положительно определенная билинейная форма.
называется евклидовым, если на нем выделена симметричная положительно определенная билинейная форма.
Другими словами, на пространстве 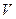 выделена билинейная форма
выделена билинейная форма 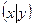 , обладающая свойствами:
, обладающая свойствами:
1). 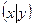 =
=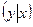 ;
;
2). 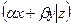 =
=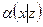 +
+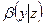 ;
;
3). 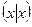
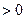 для всех
для всех 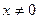 .
.
Примеры. 1). Скалярное произведение в обычном трехмерном пространстве геометрических векторов превращает его в евклидово пространство.
В общем случае эту выделенную форму на произвольном пространстве тоже будем называть скалярным произведением.
2). Пусть 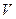 - арифметическое векторное пространство строк длины
- арифметическое векторное пространство строк длины 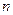 . Введем на
. Введем на 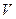 скалярное произведение следующим образом. Если
скалярное произведение следующим образом. Если 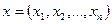 ,
, 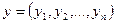 , то
, то 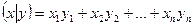 . Легко проверить, что эта форма билинейная, симметричная и положительно определенная.
. Легко проверить, что эта форма билинейная, симметричная и положительно определенная.
3). Пусть 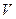 - линейное пространство функций, непрерывных на отрезке
- линейное пространство функций, непрерывных на отрезке 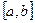 . Можно задать скалярное произведение в этом пространстве таким образом:
. Можно задать скалярное произведение в этом пространстве таким образом:
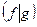
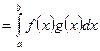 .
.
16.2. Длина вектора в евклидовом пространстве. Пусть 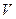 - евклидово пространство со скалярным произведением
- евклидово пространство со скалярным произведением 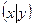 .
.
Определение. Длиной (нормой) вектора 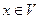 будем называть неотрицательное действительное число
будем называть неотрицательное действительное число
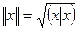 .
.
Заметим, что если 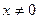 , то
, то 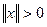 . Далее,
. Далее, 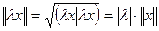 ,
, 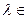 R.
R.
Вектор длины 1 называют нормированным. Любой вектор можно нормировать, умножив его на подходящее число, а именно для вектора 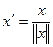 имеем:
имеем:
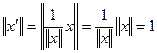 .
.
 2014-02-09
2014-02-09 1112
1112