Аналитическое описание процедуры измерений

Аналитическое описание процедуры измерений осуществляется с помощью уравнения измерений, связывающего между собой: истинное значение измеряемой величины х; результат измерения x_N=N_xq_k= N_xq_x, где q_k - ступень квантования, единица младшего десятичного разряда числового значения меры N_x, обычно равная десятичной кратной или дольной единице измеряемой величины q_x; погрешность измерения D=x_N-x; числовое значение кода меры N_x; ступень квантования q_k; коэффициент масштабного преобразования К_мп. Уравнение измерений получают из уравнения устройства сравнения подстановкой в него уравнения меры и масштабного преобразователя.

Процедура измерений может быть построена по самым различным алгоритмам. Для пояснения общих принципов составления уравнения измерений рассмотрим [6] простейший случай, когда процедуру измерений составляют лишь две операции: операция воспроизведения мерой ряда величин с известными размерами из множества x_N, т.е. x₁, x₂…x₁…x_Nн, например, равноинтервального ряда с одинаковым интервалом q_k, размер которого принимаем равным единице данной величины или ее десятичной доле; операция сравнения для выявления знака разности размеров величины х и однородной выходной величины x_N.

В этом случае операция воспроизведения величины заданного размера реализуется в виде ступенчатого изменения известной величины x_Ni последовательными шагами от первого i=1 до конечного i_кон. Размеры ступеней x_i при отработке выбирают в зависимости от способа отработки – равномерно- или неравномерно-ступенчатого. Если используется равномерно-ступенчатое изменение известной величины, то ступень изменения равна ступени квантования q_k; если изменение x_i неравномерно-ступенчатое, то в начале изменение происходит большими ступенями x_i, а затем меньшими, вплоть до q_k. Отработка x_N продолжается до тех пор, пока не уравняется х и x_Nx, т.е. до тех пор, пока разность x_N-x не станет меньше минимальной ступени q_k.

Операция отработки может быть записана следующим образом:

,

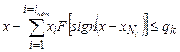где x_i - изменение образцовой величины x_N при i -м шаге отработки;

где x_Ni - значение величины x_N после i -го шага отработки.

На конечном шаге отработки имеем:

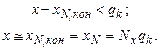(5.6)

Числовое значение величины, следовательно:

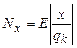, (5.7)

где Е – целая часть числа, полученного делением х на q_х.

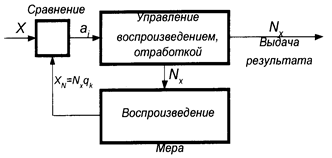
Выражение (5.7), описывающее зависимость между числовым значением результата измерения N_x и размером измеряемой величины х, и является уравнением измерений. Рассмотренный алгоритм может быть представлен структурной схемой, приведенной на рис. 5.4.

Рис. 5.4. Структурная схема непосредственных

прямых измерений

Составим уравнение измерений для трех вариантов набора элементарных средств измерений, реализующих операции измерительной процедуры.

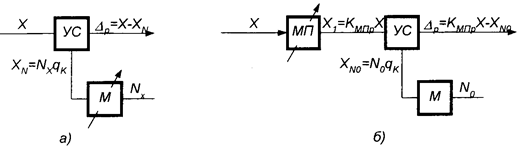
В первый вариант набора входят одноканальная регулируемая мера и устройство сравнения (рис. 5.5, а).

Рис. 5.5. Простейшие наборы средств измерений для реализации абсолютных непосредственных измерений: а - устройство сравнения (УС) и одноканальная регулируемая мера (М); б - устройство сравнения, одноканальная нерегулируемая мера и одноканальный регулируемый масштабный преобразователь(МП)

Подставим в уравнение устройства сравнения уравнение меры:

x – x_n =D_p; x - N_xq_k £ q_k.

Для нахождения х нужно изменять N_x до тех пор, пока D_p не станет меньше q_k. Очевидно, мера должна быть многозначной во всем диапазоне х:

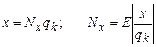. (5.8)

Следовательно, измерение математически представляется в виде деления, которое продолжается, пока остаток деления или разность становится:

x - N_xq_k < q_k.

Уравнение измерения 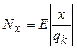всегда является линейным, так как .

Второй вариант состава элементарных средств измерений включает нерегулируемую одноканальную меру, устройство сравнения и масштабный преобразователь (рис. 5.5, б). Уравнение измерения получаем подстановкой в уравнение устройства сравнения уравнения масштабного преобразователя:

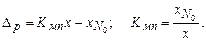
Если выполнить условие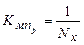, то

,

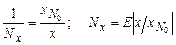т.е. уравнение измерений линейно. Однако соблюсти это условие затруднительно и поэтому такой вариант применяется редко.

Третий рассматриваемый нами вариант предполагает наличие в составе элементарных средств измерений регулируемой одноканальной меры, устройства сравнения, масштабного преобразователя, тогда:

Поскольку K_мпр=const - уравнение измерений линейно.