Пусть 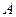 – произвольная точка аффинного пространства
– произвольная точка аффинного пространства 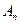 , а
, а 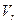 - некоторое подпространство векторного пространства
- некоторое подпространство векторного пространства 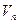 , связанного с
, связанного с 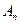 (подпространство есть множество векторов, само являющееся пространством относительно заданных на исходном пространстве операций).
(подпространство есть множество векторов, само являющееся пространством относительно заданных на исходном пространстве операций).
Определение 1: множество точек полученных при откладывании от точки 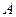
всех векторов подпространства 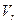 называется r-мерной плоскостью, натянутой на точку
называется r-мерной плоскостью, натянутой на точку 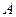 и подпространство
и подпространство 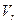 и обозначается
и обозначается 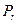 . Подпространство
. Подпространство 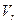 называется направляющим подпространством плоскости
называется направляющим подпространством плоскости 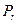 .
.
Выберем в подпространстве 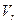 какой – либо базис
какой – либо базис 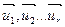 , и будем говорить, что плоскость
, и будем говорить, что плоскость 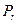 натянута на точку
натянута на точку 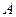 и векторы
и векторы 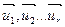 . Тогда плоскость
. Тогда плоскость 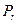 можно определить как множество таких точек
можно определить как множество таких точек 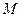 , что
, что
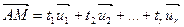 , (1)
, (1)
где коэффициенты (параметры) принимают независимо друг от друга всевозможные действительные значения.
Замечание 1: при 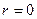 подпространство
подпространство 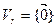 - состоит только из нулевого вектора, а плоскость
- состоит только из нулевого вектора, а плоскость 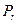 - только из точки
- только из точки 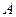 . Поэтому любую точку будем рассматривать как нуль - мерную плоскостью
. Поэтому любую точку будем рассматривать как нуль - мерную плоскостью
Определение 2: при 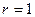 имеем одномерную плоскость, которую назовем прямой и обозначим
имеем одномерную плоскость, которую назовем прямой и обозначим 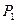 . При
. При 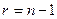 получим
получим 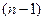 - мерную плоскость, назовем ее гиперплоскостью и обозначим
- мерную плоскость, назовем ее гиперплоскостью и обозначим 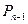 .
.
Замечание 2: если 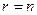 , то получаем базис
, то получаем базис 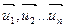 всего векторного пространства
всего векторного пространства 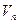 , поэтому все пространство
, поэтому все пространство 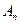 можно считать n-мерной плоскостью.
можно считать n-мерной плоскостью.
Пример: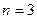 , для пространства
, для пространства 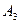 введенные выше по определению понятия уже знакомы из школьного курса геометрии (они были там основными, неопределяемыми).
введенные выше по определению понятия уже знакомы из школьного курса геометрии (они были там основными, неопределяемыми).
При 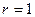 прямая
прямая 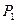 задается уравнением:
задается уравнением:
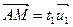 ,
, 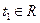
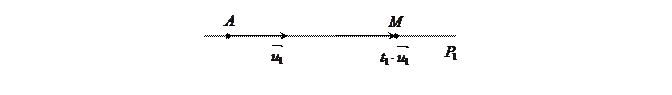
При 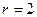 двумерная плоскость
двумерная плоскость 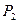 , являющаяся гиперплоскостью пространства
, являющаяся гиперплоскостью пространства 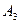 (в школе она называлась просто плоскостью), задается уравнением:
(в школе она называлась просто плоскостью), задается уравнением:
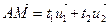 ,
, 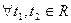 .
.

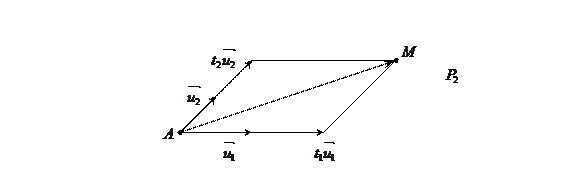
Определение 3: Множество точек 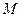 из
из 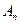 таких, что равенство (1) выполняется при
таких, что равенство (1) выполняется при 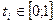 ,
, 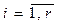 называется r – мерным параллелепипедом, натянутым на точку
называется r – мерным параллелепипедом, натянутым на точку 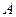 и векторы
и векторы 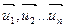 .
.
Определение 4: одномерный параллелепипед называется отрезком и задается уравнением:
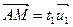 ,
, 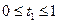 .
.
Точки 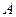 и
и 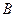 , получаемые соответственно при
, получаемые соответственно при 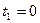 и при
и при 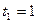 , называются концами отрезка.
, называются концами отрезка.
Если 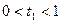 , то получаются внутренние точки отрезка
, то получаются внутренние точки отрезка 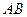 .
.
Точка 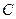 , получаемая при
, получаемая при 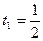 , называется серединой отрезка
, называется серединой отрезка 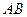 , а точки
, а точки 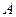 и
и 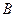 называются симметричными относительно
называются симметричными относительно 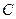 .
.
Определение 5: число 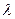 такое что
такое что 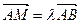 , называется отношением, в котором точка
, называется отношением, в котором точка 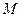 делит отрезок
делит отрезок 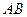 .
.
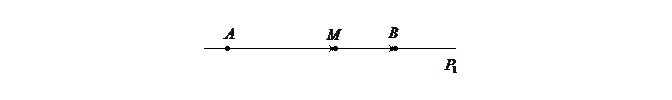
Для этого рисунка: 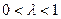 .
.
2º Плоскость как аффинное пространство
Роль точки 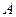 в определении многомерной плоскости может играть любая другая точка этой плоскости.
в определении многомерной плоскости может играть любая другая точка этой плоскости.
Теорема 1: если плоскость 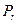 натянута на точку
натянута на точку 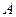 и подпространство
и подпространство 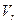 , то она также натянута на это подпространство и любую другую свою точку
, то она также натянута на это подпространство и любую другую свою точку 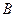 .
.
□ Обозначим через 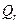 плоскость натянутую на
плоскость натянутую на 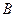 и
и 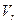 . Требуется доказать, что
. Требуется доказать, что 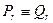 , то есть что всякая точка, принадлежащая одной плоскости, принадлежит также и другой.
, то есть что всякая точка, принадлежащая одной плоскости, принадлежит также и другой.
1) Пусть 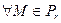 , тогда
, тогда 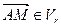 . Так как
. Так как 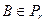 , то и
, то и 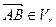 . По аксиоме треугольника II имеем:
. По аксиоме треугольника II имеем:
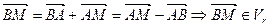 , то есть
, то есть 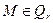 .
.
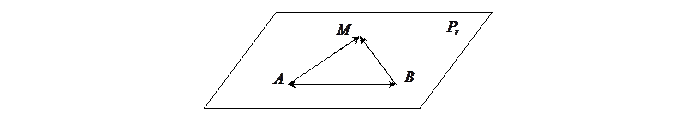
2) Обратно, пусть 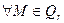 , тогда
, тогда 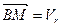 . Так как
. Так как 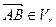 , то
, то 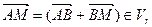 , то есть
, то есть 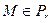 . ■
. ■
Теорема 2: всякая r – мерная плоскость является r – мерным аффинным пространством.
□ Пусть 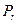 - плоскость, натянутая в пространстве
- плоскость, натянутая в пространстве 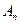 на точку
на точку 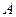 и подпространство
и подпространство 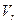 . Выберем в
. Выберем в 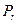 две произвольные точки
две произвольные точки 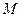 и
и 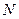 , тогда
, тогда 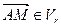 и
и 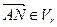 , следовательно:
, следовательно: 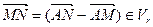 .
.
Таким образом, каждой упорядоченной паре точек 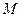 и
и 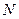 плоскости
плоскости 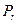 соответствует определенный вектор
соответствует определенный вектор 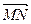 ее направляющего подпространства
ее направляющего подпространства 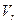 . Из определения r – мерной плоскости и теоремы (1) следует, что для
. Из определения r – мерной плоскости и теоремы (1) следует, что для 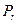 выполняется аксиома I. Аксиома треугольника II, является справедливой для любых точек пространства
выполняется аксиома I. Аксиома треугольника II, является справедливой для любых точек пространства 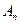 , выполняется в частности и для плоскости
, выполняется в частности и для плоскости 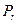 . ■
. ■
§4. Способы задания многомерной плоскости
1º Векторные уравнения.
Пусть в пространстве 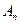 плоскость
плоскость 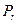 натянута на точку
натянута на точку 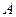 и линейно независимые векторы
и линейно независимые векторы 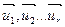 . Тогда по определению она состоит из таких точек
. Тогда по определению она состоит из таких точек 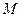 , что:
, что:
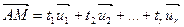 , (1)
, (1)
где 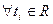 ,
, 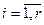 .
.
Для трех точек 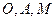 из
из 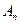 по аксиоме треугольника II имеем:
по аксиоме треугольника II имеем:
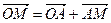 или
или
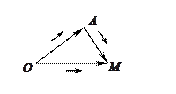
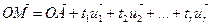 . (2)
. (2)
Уравнения (1) и (2) называются векторными уравнениями плоскости 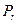 .
.
2º Параметрические уравнения

Пусть в некоторой АСК 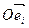 точка
точка 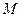 имеет координаты
имеет координаты 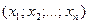 , точка
, точка 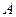 имеет координаты
имеет координаты 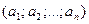 , векторы
, векторы 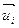 имеют в базисе
имеют в базисе 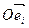 следующие координаты:
следующие координаты:
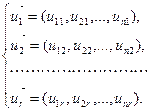
Тогда, подставляя соответствующие разложения векторов: 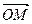 ,
, 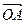 ,
, 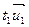 ,
, 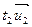 , …,
, …, 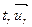 в уравнение (2) и приравнивая в левой и правой частях коэффициенты при одинаковых координатных векторах, получаем систему линейных уравнений:
в уравнение (2) и приравнивая в левой и правой частях коэффициенты при одинаковых координатных векторах, получаем систему линейных уравнений:
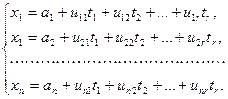 (3)
(3)
Уравнения (3) выражают текущие координаты 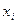 точек
точек 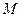 плоскости
плоскости 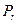 с помощью линейных функций от
с помощью линейных функций от 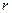 параметров
параметров 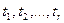 и называются параметрическими уравнениями этой плоскости. В случае
и называются параметрическими уравнениями этой плоскости. В случае 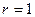 для прямой
для прямой 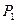 имеем:
имеем:
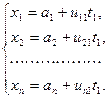
 (4)
(4)
Исключив параметр 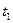 , получаем:
, получаем:
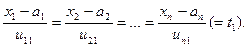 (5)
(5)
При 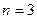 имеем уже знакомые канонические уравнения прямой
имеем уже знакомые канонические уравнения прямой 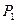 .
.
3º Общие уравнения
Исключить параметры 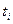 из уравнения (3) можно и в случае плоскости любой размерности
из уравнения (3) можно и в случае плоскости любой размерности 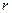 ,
, 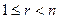 .
.
Опишем этот прием.
1) Какие - либо 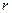 уравнений из системы (3) разрешим относительно параметров
уравнений из системы (3) разрешим относительно параметров 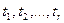 , то есть выразим их через переменные
, то есть выразим их через переменные 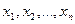 . Это возможно, так как векторы
. Это возможно, так как векторы 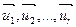 линейно независимы, значит
линейно независимы, значит
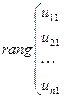
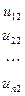
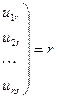 .
.
Тогда хотя бы один минор этой матрицы порядка 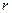 отличен от нуля.
отличен от нуля.
2) Подставим полученные выражения для 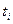 в оставшиеся
в оставшиеся 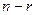 уравнений, при
уравнений, при
этом получим систему из 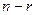 уравнений с переменными
уравнений с переменными 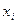 (не обязательно всеми!), не содержащую параметров
(не обязательно всеми!), не содержащую параметров 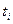 :
:
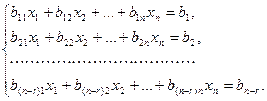 (6)
(6)
Так как точка 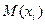 принадлежит плоскости
принадлежит плоскости 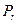 тогда и только тогда, когда ее координаты удовлетворяют полученным уравнениям, то уравнения (6) называются общими уравнениями этой плоскости.
тогда и только тогда, когда ее координаты удовлетворяют полученным уравнениям, то уравнения (6) называются общими уравнениями этой плоскости.
Итак, любая плоскость 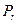 ,
, 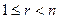 , в аффинном пространстве
, в аффинном пространстве 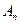 может быть задана системой
может быть задана системой 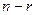 линейных уравнений. В частности, для гиперплоскости
линейных уравнений. В частности, для гиперплоскости 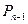 :
: 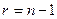 ,
, 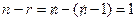 , то есть она может быть задана одним линейным уравнением.
, то есть она может быть задана одним линейным уравнением.
Замечание 1: так как параметры можно исключить из системы (3) по-разному, то, то одна и та же плоскость 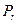 , может задаваться различными системами линейных уравнений.
, может задаваться различными системами линейных уравнений.
Замечание 2: перейти от системы вида (6) к уравнениям вида (3) и далее к уравнениям (2) и (1) можно в обратном порядке, например, положив: 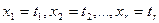 .
.
Пример: составить различные уравнения плоскости 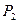 , натянутой в аффинном пространстве
, натянутой в аффинном пространстве 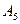 на точку
на точку 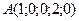 и векторы
и векторы 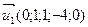 ,
, 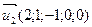 .
.
Решение: Так как соответствующие координаты векторов 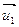 и
и 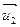 не пропорциональны, то эти векторы не коллинеарны, следовательно, линейно независимы и являются направляющими векторами пространства
не пропорциональны, то эти векторы не коллинеарны, следовательно, линейно независимы и являются направляющими векторами пространства 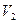 , связанного с
, связанного с 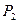 .
.
1)  ,
, 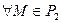 - векторное уравнение.
- векторное уравнение.
2) 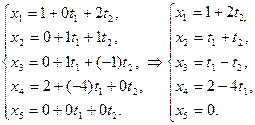 - параметрические уравнения.
- параметрические уравнения.
3) Из 2-го и 3-го уравнения выразим 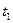 и
и 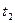 :
: 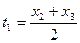 ,
, 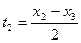 .
.
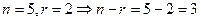 .
.
Подставим эти выражения в оставшиеся три уравнения:
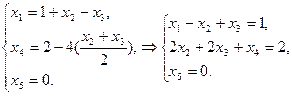 - общие уравнения.
- общие уравнения.
Другой способ исключения параметров 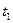 и
и 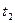 дает другой результат:
дает другой результат:
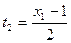 ,
, 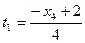 :
:
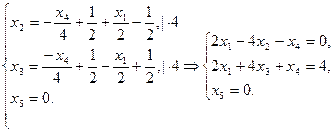
§5. Взаимное расположение многомерных плоскостей
Рассмотрим в аффинном пространстве 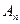 две плоскости
две плоскости 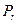 и
и 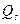 , где
, где 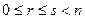 , с направляющими подпространствами
, с направляющими подпространствами 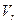 и
и 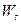 .
.
Определение 1: плоскости 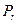 и
и 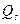 называются параллельными, если направляющие подпространства одной из них (меньшей по размерности) содержится в направляющем подпространстве другой плоскости.
называются параллельными, если направляющие подпространства одной из них (меньшей по размерности) содержится в направляющем подпространстве другой плоскости.
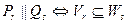 .
.
Определение 2: если плоскости Pr и Qs не параллельны и имеют хотя бы одну точку, то они называются пересекающимися.
Определение 3: если плоскости Pr и Qs не параллельны и не имеют общих точек, то они называются скрещивающимися.
Теорема 1: если две плоскости пересекаются, то их пересечение есть плоскость, направляющее подпространство которой является пересечением направляющих подпространств этих плоскостей. [3], §4, c.18, Т.1.
□ Пусть Pr натянута на точку А и подпространство Vr, а Qs натянута на точку B и подпространство Ws. Пусть C  Pr ∩ Qs – их общая точка, обозначим Vr ∩ Ws = Up , а Тр – плоскость, натянутую на C и Up.
Pr ∩ Qs – их общая точка, обозначим Vr ∩ Ws = Up , а Тр – плоскость, натянутую на C и Up.
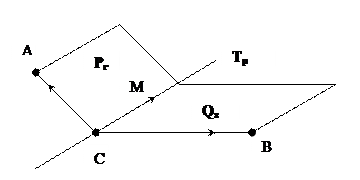
Докажем, что Tp = Pr ∩ Qs.
1) Пусть  M
M Tp, тогда
Tp, тогда 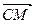
 Up = Vr ∩ Ws, значит
Up = Vr ∩ Ws, значит 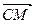
 Vr и
Vr и 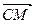
 Ws, то есть M
Ws, то есть M  Pr и M
Pr и M  Qs, поэтому M
Qs, поэтому M  Pr ∩ Qs.
Pr ∩ Qs.
2) Обратно: если M  Pr ∩ Qs, то M
Pr ∩ Qs, то M  Pr и M
Pr и M  Qs, откуда
Qs, откуда 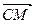
 Vr и
Vr и 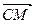
 Ws, следовательно:
Ws, следовательно: 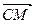
 Up = Vr ∩ Ws, тогда M
Up = Vr ∩ Ws, тогда M Tp. ■
Tp. ■
Теорема 2: если две плоскости параллельны и пересекаются, то одна из них (меньшей размерности) принадлежит другой (большей размерности). [3], §4, c.19, Т.2.
□ Пусть Pr || Qs и С = Pr ∩ Qs, где для определенности r ≤ s. Тогда по определению параллельности Vr 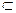 Ws. Докажем, что Pr
Ws. Докажем, что Pr 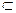 Qs, то есть что любая точка M
Qs, то есть что любая точка M  Pr принадлежит также и Qs.
Pr принадлежит также и Qs.
Пусть M  Pr, тогда
Pr, тогда 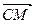
 Vr, но Vr
Vr, но Vr 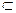 Ws, значит
Ws, значит 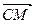
 Ws или M
Ws или M  Qs. ■
Qs. ■
Пример 1: n = 3, A3 – трехмерное аффинное пространство, r = 1, s = 2, прямая P1 и двумерная плоскость Q2.
1) P1 || Q2 и не имеют общих точек (в школьных учебниках - параллельны):
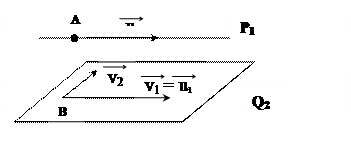
2) P1 || Q2 и имеют общие точки 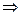 P1
P1 Q2:
Q2:
В каждом из этих случаев V1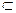 W2, причем векторы
W2, причем векторы 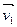 и
и 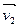 базиса подпространства W2 можно выбрать так, что вектор будет базисным вектором и для подпространства V1.
базиса подпространства W2 можно выбрать так, что вектор будет базисным вектором и для подпространства V1.
 3) P1 || Q2
3) P1 || Q2 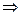 они имеют единственную общую точку С, найти ее координаты можно, решив совместно уравнения, задающие прямую P1 и плоскость Q2.
они имеют единственную общую точку С, найти ее координаты можно, решив совместно уравнения, задающие прямую P1 и плоскость Q2.

Таким образом, в A3 плоскости P1 и Q2 не могут скрещиваться (однако, в пространстве A4 это возможно).
4) P1 и Q1, r = s = 1.


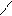
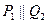 и
и 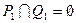
 P1 · Q2
P1 · Q2  – скрещиваются.
– скрещиваются.
Заметим, что: 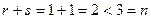 .
.
Пример 2: в пространстве A5 исследовать взаимное расположение прямой P1 – оси Ox аффинной системы координат 
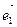
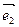
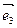
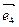
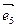 – и плоскости Q2, натянутой на точку B(-1;0;0;0;0) и векторы
– и плоскости Q2, натянутой на точку B(-1;0;0;0;0) и векторы 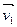 (0;1;0;2;0) и
(0;1;0;2;0) и
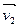 (0;1;0;-1;1)
(0;1;0;-1;1)
Решение: 1) Установим, параллельны ли P1 и Q2.
Прямая P1 натянута на точку 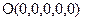 и третий координатный вектор
и третий координатный вектор 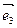 =
=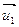 =(0;0;1;0;0). Найдем ранг матрицы из координат векторов
=(0;0;1;0;0). Найдем ранг матрицы из координат векторов 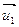 ,
, 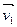 ,
, 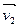 :
:









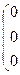
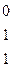
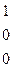
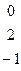
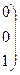 ~
~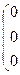
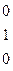
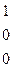
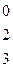
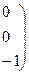
 r=3
r=3  векторы линейно независимы,
векторы линейно независимы,
|
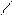 вектор
вектор 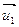 не может быть линейной комбинацией векторов
не может быть линейной комбинацией векторов 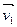 и
и 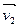 значит V1
значит V1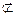 W2 и P1 || Q2.
W2 и P1 || Q2.
2) Установим, имеют ли эти плоскости общие точки, для чего решим совместно их параметрические уравнения:

 P1:
P1: 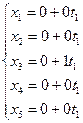 , Q2:
, Q2: 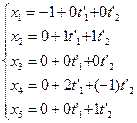 .
.
Сравним первые уравнения (x1 = 0 и x1 = -1), замечаем, что система несовместна, общих точек нет, плоскости P1 и Q2 скрещиваются:
 P1 · Q2.
P1 · Q2.
Замечание: имеет место теорема: для скрещивающихся плоскостей аффинного пространства сумма их размерностей меньше размерности пространства, то есть плоскости Pr и Qs пространства 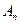 не могут скрещиваться, если r + s ≥ n.
не могут скрещиваться, если r + s ≥ n.
(Плоскости Pr и Qs пространства 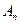 могут скрещиваться тогда и только тогда, когда r + s < n. Если n>1, то гиперплоскости не могут скрещиваться).
могут скрещиваться тогда и только тогда, когда r + s < n. Если n>1, то гиперплоскости не могут скрещиваться).
 2014-02-24
2014-02-24 6629
6629
