Пусть имеется отображение 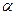 аффинного пространства
аффинного пространства 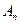 на аффинное пространство
на аффинное пространство 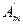 , при котором для точек M, N
, при котором для точек M, N  An
An 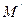 =
=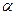 (M),
(M), 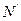 =
=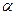 (N), причем
(N), причем  – некоторое отображение векторного пространства
– некоторое отображение векторного пространства 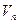 на векторное пространство
на векторное пространство 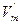 :
:  :
: 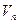
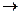
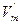 .
.
Определение 1: отображение  называется ассоциированным с отображением
называется ассоциированным с отображением 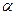 , если при любом выборе точек M и N оно отображает вектор
, если при любом выборе точек M и N оно отображает вектор 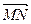 на вектор
на вектор 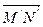 :
:
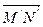 =
=  (
(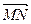 ).
).
Определение 2: взаимно однозначное отображение 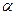 аффинного пространства An на аффинное пространство
аффинного пространства An на аффинное пространство 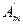 называется изоморфизмом, если существует ассоциированное с ним изоморфное отображение
называется изоморфизмом, если существует ассоциированное с ним изоморфное отображение  пространства
пространства 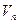 на пространство
на пространство 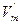 (оно биективно и
(оно биективно и  (
(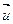 +
+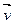 )=
)= (
(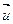 )+
)+ (
(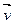 ),
),  (k
(k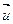 ) = k
) = k (
(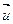 ) – линейно).
) – линейно).
Определение 3: аффинные пространства An и 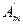 называются изоморфными, если существует изоморфное отображение одного из них на другое:
называются изоморфными, если существует изоморфное отображение одного из них на другое: 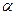 (
(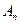 ) =
) = 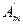 или
или 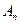
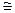
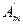 .
.
Теорема (Признак изоморфизма аффинных пространств): для того, чтобы два аффинных пространства 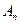 и
и 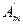 были изоморфны, необходимо и достаточно, чтобы их размерности были одинаковыми.
были изоморфны, необходимо и достаточно, чтобы их размерности были одинаковыми.
□ Необходимость. Пусть пространства 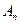 и
и 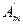 изоморфны, тогда по определению (2) связанные с ними векторные пространства также изоморфны и поэтому имеют одинаковые размерности; но тогда совпадают и размерности пространств An и
изоморфны, тогда по определению (2) связанные с ними векторные пространства также изоморфны и поэтому имеют одинаковые размерности; но тогда совпадают и размерности пространств An и 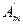 , то есть n = m.
, то есть n = m.
Достаточность. Пусть аффинные пространства 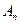 и
и 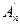 имеют одну и ту же размерность n, докажем, что они изоморфны.
имеют одну и ту же размерность n, докажем, что они изоморфны.
Введем в этих пространствах аффинные системы координат и устроим биективное отображение 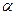 пространства An на пространство
пространства An на пространство 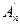 следующим образом: M(xi)
следующим образом: M(xi)  An
An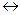
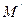 (xi)
(xi) 
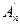
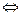 xi =
xi = 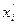 , (i = 1, 2, …, n).
, (i = 1, 2, …, n).
Покажем, что отображение 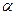 есть изоморфизм.
есть изоморфизм.
Рассмотрим отображение  пространств
пространств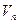 и
и 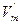 , связанных с An и
, связанных с An и 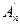 , при котором соответствующими считаются векторы, которые имеют во введенных аффинных системах одинаковые координаты. Это отображение
, при котором соответствующими считаются векторы, которые имеют во введенных аффинных системах одинаковые координаты. Это отображение  является ассоциированным с отображением
является ассоциированным с отображением 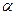 . Действительно, пусть образами точек M(xi) и N(yi) при отображении
. Действительно, пусть образами точек M(xi) и N(yi) при отображении 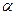 являются соответственно точки
являются соответственно точки 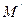 (
(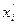 ) и
) и 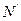 (
(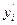 ). Так как xi =
). Так как xi = 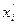 и yi =
и yi = 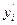 , то имеем:
, то имеем: 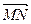 =(yi - xi)=(
=(yi - xi)=(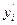 -
- 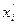 )=
)=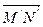 то есть вектор
то есть вектор 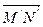 является образом вектора
является образом вектора 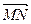 при отображении
при отображении  .
.
Докажем, что  - изоморфное отображение
- изоморфное отображение 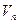 на
на 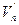 . Так как оно биективно, то достаточно убедиться в его линейности.
. Так как оно биективно, то достаточно убедиться в его линейности.
Пусть 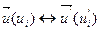 ,
, 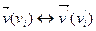 , тогда
, тогда 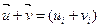 ,
, 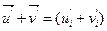 , a так как
, a так как 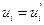 и
и 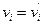 , то
, то 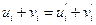 , следовательно, вектор
, следовательно, вектор 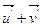 является образом вектора
является образом вектора 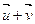 при
при  .
.
Аналогично, образом вектора 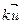 является вектор
является вектор 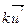 . Итак, отображение
. Итак, отображение  :
: 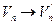 - изоморфизм. Согласно определениям (2) и (3) пространства
- изоморфизм. Согласно определениям (2) и (3) пространства 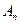 и
и 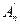 изоморфизмы. ■
изоморфизмы. ■
 2014-02-24
2014-02-24 2435
2435








