Решение систем линейных уравнений

END.

REPEAT

Begin

Begin

Begin

END.

Else

REPEAT

Begin

Begin

VAR

End.

REPEAT

Begin

Begin

VAR

xp, e, x0, x:REAL;

Function f(x:real): real;

f:= x*x-2;

end;

writeln('введите начальное приближение х и точность');

read(x0,e);

x:=x0;

xp:=x;

x:=f(x);

UNTIL ABS(x-xp)<e;

writeln('корень уравнения =', x);

В данной программе используется подпрограмма функция f, которая вычисляет левую часть преобразованного уравнения:

^.

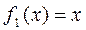Переменная xp используется в программе для сохранения предыдущего значения х.

Численное решение нелинейных уравнений
методом бисекции

Метод сос­то­ит в по­стро­е­нии по­­­сле­­до­ва­тель­ности вло­жен­ных от­рез­ков, на кон­­цах ко­то­рых F(х) имеет разные зна­ки. Каж­дый по­­­сле­­ду­ю­щий от­ре­зок получают де­ле­ни­­ем по­по­лам пре­ды­ду­­ще­го. Этот процесс по­стро­е­ния по­­­сле­­до­­ва­тель­нос­ти вло­жен­ных отрезков по­зво­ляет най­­­ти нуль функ­ции (F(х) = 0) с лю­бой за­дан­ной точ­­­ностью.

Опишем подробно один шаг итерации (рис. 28). Пусть на k-м ша­ге найден отрезок [а_k, b_k], на концах ко­­то­рого F(х) меняет знак. Заметим, что обязательно [а_k, b_k] Î [а, b].

1. Разделим те­перь отрезок [а_k, b_k] пополам и вы­де­­лим F(c_k), где c_k – се­ре­ди­­на [а_k, b_k].

2. Здесь воз­мож­­ны два слу­чая:

§ первый, ког­да F(c_k) = 0, тогда мы го­ворим, что ко­рень найден;

§ вто­рой, ког­да F(c_k) ¹ 0, тог­да срав­­ниваем знак F(c_k) с F(а_k) и F(b_k) и из двух по­­ло­­вин [аk, c_k] и [c_k, bk] вы­бираем ту, на концах ко­то­рой функ­ция меняет свой знак. Та­ким образом, а_k+1 = а_k, b_k+1 = c_k, если F(c_k)F(а_k) < 0 (рис. 27), и а_k+1 = c_k, b_k+1 = b_k, ес­ли F(c_k)F(b_k) < 0.

При заданной точности e деление пополам про­­­­­­дол­жа­ют до тех пор, пока длина отрезка не ста­­­­­нет меньше 2e, тогда координата середины по­­след­­­­него най­­­денного от­резка и есть значение кор­­ня тре­бу­е­мой точ­ности.

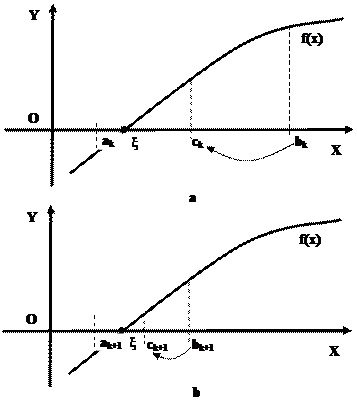
Рисунок 28 – Геометрическая интерпретация решения уравнения методом бисекции
a) k–й шаг; b) k+1-й шаг.

Приведём программу, реализующую итерационный метод уточнения корня уравнения:

^.

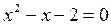program Bisect;

A,B,E:REAL; X: REAL;

Function f(x:real): real;

f:= x*x-x-2;

end;

writeln('введите отрезок локализации корня [a,b] и точность');

read(a,b,e);

k:=0;

X:= (A+B)*0.5;

IF f(X)*f(B)<0 THEN

a:=x

b:=x

UNTIL ABS(B-A)<e;

writeln('корень уравнения =', (A+B)*0.5);

В данной программе используется подпрограмма функция f, которая вычисляет левую часть исходного уравнения:

^.

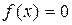Переменная x используется в программе для сохранения значения середины отрезка [a, b].

Численное решение нелинейных уравнений
методом Ньютона

Положим:

,

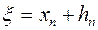где x – корень уравнения f(x) = 0, h_n считаем малой величиной. Отсюда, применяя формулу Тейлора, получим:

.

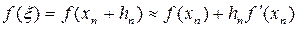Следовательно, 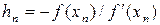. Подставив это выражение, получим:

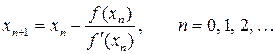
Геометрическая интерпретация метода представлена на рисунке 29.

Через точку А₀(х,у) с координатами х = x₀, у = f(x₀) про­водим ка­са­тель­­ную. По формуле

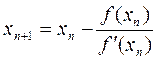
на­ходим точку пересечения касательной с осью ОХ (точ­к­а х₁).

Находим точку А₁(х₁,у), проводим касательную через точку А₁ для нахождения х₂.

Этот процесс продолжаем до тех пор, пока разница |х_i+1-x_i| не станет меньше, чем значение e, т.е. пока не будет найдено значение корня с заданной точностью e.

Рисунок 29 – Геометрическая интерпретация решения уравнения методом Ньютона

Приведём программу, реализующую итерационный метод уточнения корня уравнения:

^.

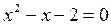program Newton;

VAR xp,E,x0:REAL; X: REAL;

Function f(x:real): real;

f:= x*x-x-2;

end;

Function df(x:real): real;

df:= 2*x-1;

end;

writeln('введите начальное приближение х и точность');

read(x0,e);

x:=x0;

xp:=x;

x:=x-f(x)/df(x);

UNTIL ABS(x-xp)<E;

writeln('корень уравнения =', x);

В данной программе используется подпрограмма функция f, которая вычисляет левую часть исходного уравнения:

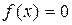
а также подпрограмма функция df, которая вычисляет значение дифференциала:

^.

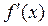Переменная xp используется в программе для сохранения предыдущего значения х.

К решению систем линейных алгебраических уравнений с большим числом неизвестных приводят многие практически важные задачи. Разработано множество методов, предназначенных для решения систем с матрицей того или иного вида. Все эти методы можно разделить на два больших класса: прямые (или точные) и итерационные.

Прямые методы дают решение системы за конечное число арифметических операций. Если коэффициенты системы не содержат погрешностей, а арифметические операции выполняются точно (без округления), то решение получается точным. Недостатки прямых методов: иногда требуется выполнение неприемлемо большого числа арифметических и логических операций; погрешности округления могут очень сильно исказить результат.

Итерационные методы позволяют получить приближенное решение с любой заданной точностью ε. Они дают искомое решение как предел последовательности приближений и различаются способами построения таких последовательностей. Недостатком этих методов является то, что построенные последовательности нередко оказываются расходящимися, т.е. конечного предела таких последовательностей может не существовать. Поэтому оказывается необходимым исследование сходимости.

Численное решение систем линейных
уравнений методом Гаусса

Система линейных алгебраических уравнений выглядит следующим образом:

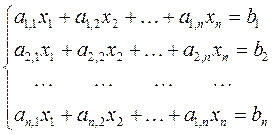
в матричной форме такая система выглядит так:

,

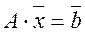где А – матица коэффициентов системы уравнений:

,

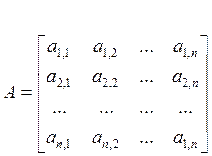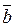– вектор свободных членов (правых частей) уравнений, 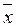– вектор неизвестных:

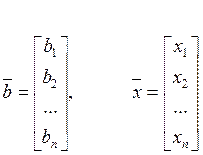
Метод Гаусса (метод последовательного исключения неизвестных) состоит из прямого и обратного хода.

В результате прямого хода матрицы системы за m преобразований приводится к треугольному виду:

.

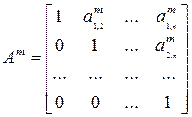Количество преобразований исходной матрицы (m) в общем случае равно количеству уравнений в системе (n).

На каждом k -ом шаге преобразования выбирается ведущая строка (k) и ведущий элемент .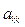

Формулы прямого хода метода Гаусса на k -ом шаге преобразования имеют следующий вид: для ведущей строки:

;

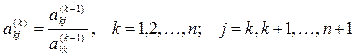для строк, лежащих под ведущей строкой:

.

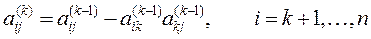Элемент 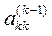называется ведущим.

Обратный ход используется для вычисления значений неизвестных.

Система уравнений с треугольной матрицей А имеет следующий вид:

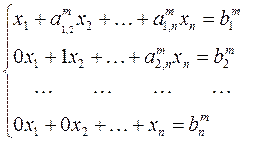
Очевидно, что

.

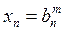Формула обратного хода метода Гаусса (нахождения остальных неизвестных в обратном порядке) имеет вид:

^.

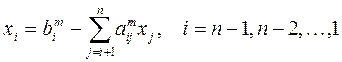При разработке программы необходимо учитывать то, что принципы индексации, принятые в математике и используемые при разработке программы, могут различаться: коэффициенту уравнения 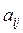соответствует элемент массива А[j,i] (см. пункт«Описания массивов» стр. 38).

Приведём программу, использующую метод Гаусса для решения системы линейных уравнений (обратите внимание на комментарии, поясняющие назначение ключевых фрагментов программы):

program gauss;

const n = 3;

var A:array[1..n,1..n]of real;

x,b:array[1..n] of real;

i,j,n,p,ii,jj:integer; aii,akk:real;