Принятие решений в условиях конфликта

Экспертные методы

Метод экспертного оценивания относится к инструментарию количественной оценки качества альтернатив в условиях слабо формализуемой проблемной ситуации.

Экспертные оценки – это качественные оценки, основанные на информации неколичественного (качественного) характера, которые могут быть получены только с помощью специалистов – экспертов. Эксперт – это высококвалифицированный специалист, полагающийся на свои знания, опыт, интуицию и умение оценивать сложные факторы (явления) и способный создать собственную обоснованную (интуитивную) модель анализируемого явления (проблемы), если он располагает необходимой для этого исходной информацией

Сущность метода экспертных оценок заключается в логико-интуитивном анализе внутренней и внешней среды организации, разработке альтернатив и количественной оценке их качества. Обобщенное мнение экспертов служит основанием для осуществления выбора.

Экспертные суждения – содержательные высказывания (определяющие состав, структуру, функциональность исследуемой системы, сущностей и их атрибутов), количественная или качественная оценка какой-либо сущности (т.е. определение количественных и качественных атрибутов и их значений).

Экспертное ранжирование. Ранжирование применяется в случаях, когда невозможна или нецелесообразна непосредственная оценка. При этом ранжирование объектов содержит лишь информацию о том, какой из них более предпочтителен, и не содержит информации о том, насколько или во сколько раз один объект предпочтительнее другого.

Ранг – степень отличия по какому-либо признаку, а ранжирование – процесс определения рангов, относительных количественных оценок степеней отличий по качественным признакам.

Используются следующие методы ранжирования: метод простой ранжировки; метод непосредственной оценки; метод парных сравнений и др.

Метод простой ранжировки. Заключается в том, что эксперты располагают объекты ранжирования (например, критерии) в порядке убывания их значимости (скажем, для альтернатив это убывание предпочтительности).

В рассмотренных в предыдущем параграфе моделях, «соперник» ЛПР, который мы называли «состоянием природы», ни как не реагировал на возможные решения ЛПР, то есть последний был ему совершенно безразличен. Однако часто таким соперником является мыслящий субъект или их группа, который осознанно выбирает вариант реализации ситуации.

Рассмотрим следующую модель. ЛПР А желает принять решение, на результат которого влияет другое ЛПР В, цели которого противоположны А. ЛПР В анализирует все возможные варианты А и принимает такое решение, которое приводит к наименьшему выигрышу А (соответственно максимальному своему выигрышу). Примерами таких ситуаций служат отношения между продавцом и покупателем, адвокатом и прокурором, кредитором и дебитором, истцом и ответчиком и т.д. Подобные ситуации называются конфликтными. Математические методы анализа конфликтных ситуаций объединяются под названием теории игр, сама конфликтная ситуация носит название игры, а стороны, участвующие в конфликте, называются игроками. Исход игры называется выигрышем (или проигрышем) игроков. Если выигрыш одного игрока равен проигрышу другого, то игра называется антагонистической. Пусть игрок А может выбрать в качестве действий одну из п альтернатив: А ₁, А ₂,…, А_n. Эти альтернативы в теории игр принято называть стратегиями. Аналогично, игрок В может принять одну из m стратегий В ₁, В ₂,…, В_m. Предположим, что известны выигрыши (проигрыши) игрока А при любой выбранной им стратегии Аi и любом ответе ему игроком В – стратегии В_j. Пусть этот результат выражен числом а_ij (которое может быть и отрицательным в случае проигрыша А). Величины а_ij образуют матрицу:

Bj Ai	B1	B2	…	S5
A1	a11	a12	…	a1m
A2	a21	a22	…	A2m
…	…		…
An	an1	an2	…	anm

Эта матрица называется платежной или матрицей игры.

Рассмотрим игру со стороны А. Он, выбирая свою стратегию А_i, понимает, что В ответит ему такой стратегией В_j, чтобы выигрыш А был минимальным. Поэтому, из всех наихудших вариантов (минимальных элементов каждой строки платежной матрицы), игроку А выгодно выбрать стратегию, соответствующую максимальному из этих элементов:

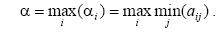
Величина 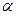называется нижней ценой игры или максимином. Это гарантированный выигрыш игрока А. С другой стороны, игрок В выбирая свою стратегию В _j понимает, что игрок А ответит такой стратегией Аi, чтобы его выигрыш был максимален. Поэтому из наилучших вариантов для А (максимальных элементов каждого столбца) 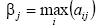игроку В рационально выбрать свою стратегию, соответствующую минимальному из этих чисел:

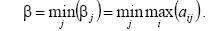
Величина 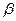называется верхней ценой игры или минимаксом. Это максимальный проигрыш игрока В. Реальный результат решения конфликтной ситуации, называемый ценой игры 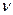, заключен между верхней и нижней ценой: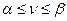. В случае, если верхняя и нижняя цены совпадают 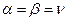, то игра имеет решение в чистых стратегиях, то есть можно точно определить стратегии 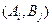, которые выгодны для обоих сторон. Если одна сторона отойдет от своей оптимальной стратегии, то ее выигрыш от этого только уменьшится.

4.8. Задача о назначениях

Задача о назначениях является типичным примером принятия управленческих решений. Сформулируем ее в общем виде. Пусть для выполнения некоторого проекта необходимы ограниченные ресурсы. Например, такими ресурсами могут выступать труд (рабочий для выполнения работы), оборудование (станок для изготовления детали), транспорт (автомобиль для перевозки груза) и т.д. Эти ресурсы предназначены для выполнения некоторых работ, причем для выполнения каждой работы требуется один и только один ресурс (один человек, одна автомашина и т.д.), а каждый ресурс может быть использован на одной и только одной работе. То есть ресурсы неделимы между работами, а работы неделимы между ресурсами. Такая задача имеет место при назначении людей на должности или работы, автомашин на маршруты, водителей на машины, при распределении групп по аудиториям, научных тем по научно-исследовательским лабораториям и т.п.

Исходные параметры модели задачи о назначениях

1. n - количество ресурсов, m - количество работ.

2. a_i = 1 - единичное количество ресурса A_i (i = 1,2,...,n),

например: один работник; одно транспортное средство; одна научная тема и т.д.

3. b_j = 1 - единичное количество работы Bj (j = 1,2,...,m), например: одна должность; один маршрут; одна лаборатория.

4. C_ij - характеристика качества выполнения работы Bj с помощью ресурса A. Например, компетентность i-го работника при работе на j-й должности; время, за которое i-е транспортное средство перевезет груз по j-му маршруту; степень квалификации i-й лаборатории при работе над j-й научной темой. Величину C_ij можно рассматривать как показатель привлекательности (критерий) для альтернативы (A_i,B_j).

В качестве исходных данных введем переменные x_ij - факт назначения или неназначения ресурса A_i на работу B_j, которая определяется по правилу:

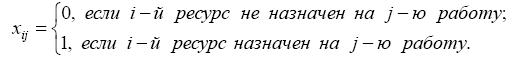
Также имеется некоторая целевая функция L(x), равная общей (суммарной) характеристики качества распределения ресурсов по работам. Это может быть прибыль или процент брака, издержки или себестоимость продукции, время производства или время эксплуатации ресурсов. Эта функция зависит от характеристик c_ij, которые образуют матрицу вида:

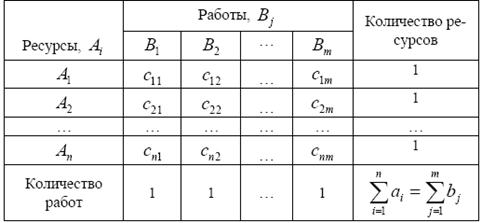
Эта матрица называется матрицей эффективностей (при максимизации целевой функции) или матрицей затрат (при минимизации). Математическая модель задачи о назначениях имеет вид:

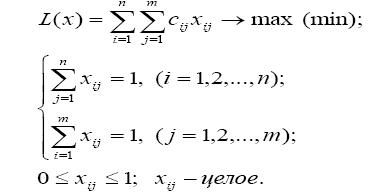
Задача о назначениях является частным случаем общих классов оптимизационных задач, и поэтому существует много разнообразных методов ее решения. История решения задачи о назначениях показывает, как постепенно математики приходили к пониманию вычислительной сложности методов, как далеко не сразу была осознана необходимость поиска эффективных алгоритмов, удобных для практического применения.

В конце 40-х годов XX века были созданы первые ЭВМ. Задача о назначениях была в ряду первых задач, которые решались с помощью компьютера. Развитие вычислительной техники привело к бурному развитию методов оптимизации. Тем временем, в 1947 году Данциг предложил очень эффективный метод для решения общей задачи линейного программирования, получивший название симплекс-метод. Задача о назначениях может быть легко сведена к задаче линейного программирования, если ввести для каждого элемента матрицы стоимостей свою переменную, принимающую значения 0 или 1, и записать 2n ограничений, что в каждом столбце и каждой строке сумма элементов строго равна единице.

В 1955 году Кун опубликовал первый аналитический алгоритм решения задачи о назначениях - венгерский метод.

Венгерский метод Куна состоит из трех шагов:

Шаг 1. Редукция матрицы.

В исходной матрице стоимостей в каждой строке определяется минимальная стоимость и вычитается от всех элементов строки. В полученной матрице в каждом столбце определяется минимальная стоимость и вычитается от всех элементов столбца. В результате, в каждой строке и в каждом столбце матрицы появятся нулевые элементы.

Шаг 2. Построение паросочетания.

Строится двудольный граф, вершины которого соответствуют строкам и столбцам матрицы, а ребра - нулевым элементам, стоящим на пересечении соответствующих строк и столбцов. Ищется наибольшее паросочетание в построенном графе. Если паросочетание окажется полным, то оно задает оптимальное решение задачи о назначениях, иначе выполняется шаг 3.

Шаг 3. Преобразование Эгервари.

В последней матрице проводится минимальное число горизонтальных и вертикальных прямых по строкам и столбцам так, чтобы в матрице вычеркнулись все нулевые элементы. Наименьший невычеркнутый элемент вычитается из всех невычеркнутых элементов и прибавляется к элементам, стоящим на пересечении проведенных прямых. В результате в матрице количество нулевых элементов увеличится.

Далее снова выполняется шаг 2.