В условиях определенности лицо, принимающее решение, знает все о возможных состояниях сущности явлений, влияющих на решение, и знает, какое решение будет принято. Лицо, принимающее решение, просто выбирает стратегию, направление действий или проект, которые дадут максимальную отдачу.
В общем случае выработка решений в условиях определенности направлена на поиск максимальной отдачи либо в виде максимизации выгоды (дохода, прибыли или полезности), либо минимизации затрат. Такой поиск называется оптимизационным анализом. Три метода оптимизации, используются лицом, принимающим решение: предельный анализ, линейное программирование и приростной анализ прибыли.
Предельный анализ. В условиях определенности доходы и затраты будут известны для любого уровня производства и продаж. Задача состоит в том, чтобы найти их оптимальное соотношение, позволяющее максимизировать прибыль. Предельный анализ позволяет сделать это. В нем используются концепции предельных затрат и предельного дохода.
Предельный доход (MR) определяется как дополнительный доход (изменение общего дохода), получаемый от продажи дополнительной единицы продукта. Графически он выражается наклоном кривой общего дохода (TR). Предельные затраты (MC) определяются как дополнительные затраты (изменение величины общих затрат) на приобретение или производство дополнительной единицы продукции. Графически они выражаются наклоном кривой общих затрат (TС). Мы должны также отметить следующее.
1. При уровнях производства Q1 и Q4 TR в точности равно ТС, так что прибыль равна нулю. Объем производства меньше Q1 или больше Q4 ведет к убыткам (т.е. характеризуется отрицательной прибылью).
2. При уровнях производства больше Ql или меньше Q4 – прибыль положительная.
3. Предельный анализ показывает, что до тех пор, пока MR превышает МС, производство и продажа дополнительной единицы продукции будут повышать прибыль. Прибыль, соответственно, максимизируется при том уровне производства, при котором MR = МС.
Приростной анализ. Приростной анализ прибыли оперирует с любыми и всеми изменениями в доходах, затратах и прибылях, явившимися следствием определенного решения. Таким образом, концепция приростного анализа охватывает изменения, как самих функций, так и их значений. Основное правило решения состоит в том, чтобы принять любое предложение, повышающее прибыль, или отвергнуть любое предложение, ее уменьшающее.
Линейное программирование. Модели линейного программирования отличаются наглядностью и относительной простотой. Их использование во многих практически важных задачах, связанных с принятием решений, оказалось высокоэффективным, в связи с чем они получили довольно широкое распространение. К числу наиболее известных задач линейного программирования относятся:
- задачи о распределении ограниченных ресурсов (задачи оптимального планирования);
- задачи об оптимальной корзине продуктов (задачи о диете, задачи оптимального смешения);
- задачи оптимального раскроя (материалов, заготовок);
- транспортные задачи;
- задачи о назначениях;
- задачи оптимизации финансовых потоков;
- задачи оптимизации графиков платежей.
4.3. принятие решений в условиях полной определенности
Рассмотрим вначале простейшую ситуацию, когда имеется полная информация о всех альтернативах по всем критериям. Данное условие в математической модели предполагает, что каждый критерий измеряется количественно и его показатель привлекательности для каждой альтернативы пропорционален его количественной оценке.
Рассмотрим вначале простейший случай, когда оценки привлекательности альтернатив по каждому критерию качественные и имеются экспертные оценки критериев по одной и той же (например десятибалльной) шкале. Пусть имеется n альтернатив и к критериев. Обозначим Uij - оценку i-й альтернативы по j-му критерию. Очевидно, что критерии имеют различную важность. Одни оказывают большее влияние на принятое в результате решение, другие меньшее. Назовем степень важности каждого критерия его весом. Пусть вес j-го критерия равен Wj. Вес критерия измеряется по любой пропорциональной шкале (например, от 0 до 1 или по десятибалльной или любой другой шкале). Веса критериев определяют либо эксперты, либо непосредственно ЛПР. Методы определения экспертных оценок альтернатив по критериям и весам критериев будут рассмотрены далее.
Итак, если известны оценки альтернатив, веса критериев и если решается задача на максимизацию, то есть чем выше оценка альтернативы, тем она более привлекательна, то для принятия оптимального решения нужно вычислить функции полезности каждой альтернативы Ft по формулам:
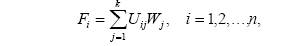
и принимается та альтернатива, для которой функция полезности максимальна. Если решается задача минимизации (чем меньше оценка альтернатив по критериям, тем привлекательнее альтернатива), то выбирается альтернатива с меньшей функцией полезности.
Экспертное оценивание методом аналитической иерархии
Несомненно, при изучении методов принятия решений в условиях определенности, возникает вопрос, а как на практике получить оценки привлекательности критериев при качественных альтернативах, как выбрать веса важности критериев. Как ранее было сказано, эти оценки осуществляет либо эксперт (специалист по исследуемому вопросу), либо ЛПР. Практических методов, согласно которым расставляются экспертные оценки, достаточно много. Простейшим (и достаточно популярным) является метод жюри, согласно которому эксперт просто-напросто, в соответствии со своими знаниями, опытом и интуицией, расставляет баллы для каждой альтернативы по имеющемуся критерию по заданной шкале.
Однако на практике не всегда можно точно и пропорционально оценить показатели привлекательности альтернатив, особенно при большом их числе. Гораздо проще бывает попарно сравнить все имеющиеся альтернативы по каждому критерию и оценить, насколько одна конкретная альтернатива привлекательнее другой. Такой метод экспертной оценки получил название метода аналитической иерархии. Рассмотрим его для случая n альтернатив, которые обозначим A1,A2,...A, и m критериев, обозначенные K1,K2,...Km. Возьмем первый критерий K1 и попарно сравним все альтернативы друг с другом по этому критерию. В результате получим матрицу сравнений 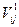 >, каждый элемент которой, в случае, если альтернатива Ai не менее предпочтительна чем альтернатива Ay равен h. Если же альтернатива Ai не более предпочтительна чем альтернатива Aj, то соответствующий элемент матрицы
>, каждый элемент которой, в случае, если альтернатива Ai не менее предпочтительна чем альтернатива Ay равен h. Если же альтернатива Ai не более предпочтительна чем альтернатива Aj, то соответствующий элемент матрицы 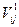 равен 1/h. Так же вычисляются матрицы сравнения
равен 1/h. Так же вычисляются матрицы сравнения 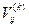 , k = 1,2,...,m для других критериев. Введем, например, такую шкалу сравнений.
, k = 1,2,...,m для других критериев. Введем, например, такую шкалу сравнений.
Шкала относительной важности парного сравнения альтернатив
| Уровень важности | Степень предпочтительности h |
| Равная важность | |
| Умеренное превосходство | |
| Существенное превосходство | |
| Значительное, большое превосходство | |
| Очень большое превосходство |
При желании можно использовать четные целые числа, выражающие промежуточные уровни предпочтительности. Следует отметить, что эксперт или ЛПР может использовать иные другие шкалы важности парных сравнений.
Аналогично, попарно сравнивая важности критериев, составляется матрица сравнения критериев по которой можно определять их веса.
На следующем этапе вычисляются собственные векторы альтернатив по всех критериям. Для каждой i-й альтернативы по к-му критерию вычисляем элемент вектора Ui k) который равен среднегеометрическому показателей матрицы сравнения для этой альтернативы (строки матрицы):
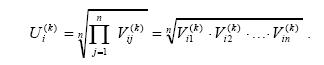
Такой же собственный вектор вычисляется и для матрицы сравнения критериев.
Далее в результате нормализации собственных векторов вычисляют веса альтернатив по каждому критерию и веса самих критериев. Вес i-й альтернативы по к-му критерию 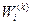 равен отношению соответствующего элемента собственного вектора к сумме всех элементов собственного вектора данного критерия:
равен отношению соответствующего элемента собственного вектора к сумме всех элементов собственного вектора данного критерия:
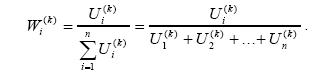
Также вычисляются и веса критериев, которые обозначим, k = 1,2,...m.
Теперь, имея оценки полезностей альтернатив по всем критериям и веса критериев можно вычислить функции полезности по каждой альтернативе и из их сравнения выбрать наилучшую альтернативу с максимальной функцией. Функция полезности i-й альтернативы вычисляется по формуле:
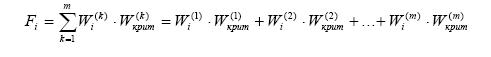
 2014-02-24
2014-02-24 3498
3498
