При выражении предпочтений на множестве предъявлений эксперты достаточно просто решают эту задачу методом попарного сравнения. Задачи обработки и анализа в этом случае заключаются в получении группового суждения об элементах множества предъявлений по результатам индивидуальных попарных сравнений. В отличие от выражения предпочтений методами ранжирования и балльного оценивания для попарного сравнения не требуется соблюдение условия транзитивности, что снимает психологические трудности восприятия экспертами различных характеристик всего множества элементов. Согласование мнений экспертов и противоречивость суждений отдельного эксперта являются первоочередными задачами обработки и анализа.
В результате попарного сравнения элементов dj Є D, 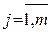 каждый из n экспертов проводит оценку всех из 0,5m(m-1) пар элементов (dj, dk) по следующему правиду:
каждый из n экспертов проводит оценку всех из 0,5m(m-1) пар элементов (dj, dk) по следующему правиду:
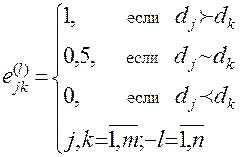 .
.
Числа 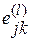 представляют из себя элементы матрицы E(l) попарных сравнений каждого из n экспертов. Полученные матрицы E(l) осредняются с учетом мнений всех экспертов:
представляют из себя элементы матрицы E(l) попарных сравнений каждого из n экспертов. Полученные матрицы E(l) осредняются с учетом мнений всех экспертов:
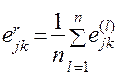 . (2.42)
. (2.42)
Числа 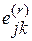 являются элементами матрицы
являются элементами матрицы 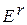 размером
размером 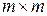 , причем
, причем 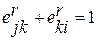 . На основе матрицы
. На основе матрицы 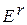 можно получить групповую ранжировку множества предъявлений, определить весовые коэффициенты (коэффициенты важности) элементов dj Є D и оценить согласованность мнений экспертов. Оценку согласованности мнений экспертов можно проводить с использованием коэффициентов вариации, вычисляемых по (2.33) − (2.34) с подстановкой вместо хl величины
можно получить групповую ранжировку множества предъявлений, определить весовые коэффициенты (коэффициенты важности) элементов dj Є D и оценить согласованность мнений экспертов. Оценку согласованности мнений экспертов можно проводить с использованием коэффициентов вариации, вычисляемых по (2.33) − (2.34) с подстановкой вместо хl величины 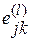 , вместо
, вместо 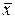 − величины
− величины 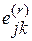 . В общем случае противоречивость суждений отдельных экспертов оценивают с использованием (2.35)−(2.37). После выполнения указанных этапов построение групповой ранжировки и определение коэффициентов важности αj,
. В общем случае противоречивость суждений отдельных экспертов оценивают с использованием (2.35)−(2.37). После выполнения указанных этапов построение групповой ранжировки и определение коэффициентов важности αj, 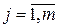 осуществляют следующим образом.
осуществляют следующим образом.
Решается уравнение вида
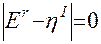 (2.43)
(2.43)
с целью отыскания собственного вектора α матрицы 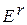 . В (2.43) η есть собственное число матрицы
. В (2.43) η есть собственное число матрицы 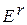 , а I – единичная диагональная матрица.
, а I – единичная диагональная матрица.
Поскольку в общем случае матрица 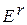 не удовлетворяет требованию транзитивности, то решение (2.43) осуществляется с помощью следующего алгоритма.
не удовлетворяет требованию транзитивности, то решение (2.43) осуществляется с помощью следующего алгоритма.
 2014-02-24
2014-02-24 909
909








