Изображение кривых 2
Лекция 3
СПИСОК ЛИТЕРАТУРЫ
[Cyrus-Beck, 1978] Cyrus M., Beck J. Generalized Two- and Three-Dimensional Clipping //Computers & Graphics.- 1978.- Vol. 3.- pp. 23-28.
[Kuzmin, 1995] Kuzmin Y.P. Bresenham's Line Generation Algorithm with Built-in Clipping //Computer Graphics Forum.- 1995.- Vol. 14, No. 5 (Dec.).
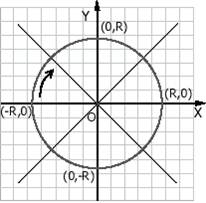 Рис. 1. Симметрии при изображении окружности.
Рис. 1. Симметрии при изображении окружности.
| Для начала перейдем к канонической системе координат, в которой центр окружности совпадает с началом координат. Тогда можно заметить, в силу симметрии окружности относительно прямых разделяющих октанты, что достаточно построить растровое представление в одном октанте, а затем с помощью симметрий получить изображения в других октантах. Будем пользоваться заданием окружности в виде неявной функции: x2+y2 - R2=0 Пусть f(x,y)= x2+y2 - R2 Будем рисовать кусок окружности в 4 октанте, начиная с точки (-R,0) Пусть R Î N, тогда f(x,y) Î Z для x Î Z, y Î Z. Пусть функция plot8 (x,y) изображает все 8 точек, полученных из (x,y) с помощью симметрий. |
Алгоритм Брезенхема. [Bresenham, 1977]
Будем рассуждать подобно алгоритму Брезенхема для отрезков (с соответствующими поправками на 4 октант). Из двух возможных пикселов в 4 октанте (соответствующих вертикальному и диагональному смещениям, см. Рис. 4) будем выбирать тот, расстояние от окружности до которого меньше.
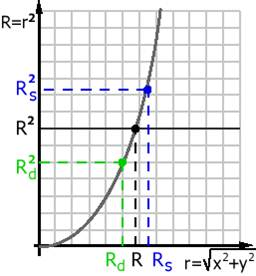 Рис. 2. Приближенное сравнение расстояний.
Рис. 2. Приближенное сравнение расстояний.
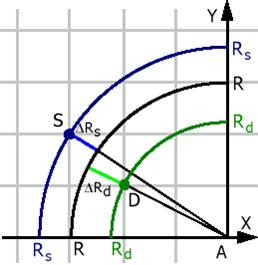 Рис. 3. Расстояния до окружности.
Рис. 3. Расстояния до окружности.
| Для того, чтобы выбрать один из двух возможных пикселов, будем сравнивать расстояния от них до окружности, где расстояние меньше - тот пиксел и будет искомым. В примере на Рис. 3 сравниваются расстояния от точек S и Dдо окружности с радиусом R.Из евклидовой метрики получаем:
DRs= 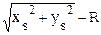 DRd=
DRd= 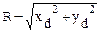 Но вычисление квадратного корня - вычислительно трудоемкая операция, поэтому при достаточно больших Rмы будем заменять сравнение расстояний сравнением приближенных значений их квадратов (см. Рис. 2):
Но вычисление квадратного корня - вычислительно трудоемкая операция, поэтому при достаточно больших Rмы будем заменять сравнение расстояний сравнением приближенных значений их квадратов (см. Рис. 2):
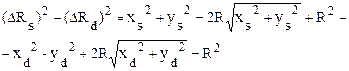 Уменьшим два слагаемых на приблизительно одинаковые величины:
Уменьшим два слагаемых на приблизительно одинаковые величины:
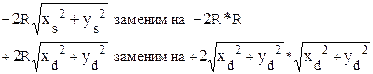 ,получим: ,получим:
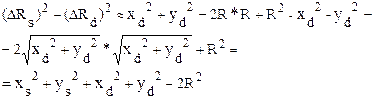 1) D ближе к окружности, чем S Û
(xs)2 + (ys)2 +(xd)2 + (yd)2 - 2*R2 > 0
2) S ближе к окружности, чем D Û
(xs)2 + (ys)2 +(xd)2 + (yd)2 - 2*R2 < 0
1) D ближе к окружности, чем S Û
(xs)2 + (ys)2 +(xd)2 + (yd)2 - 2*R2 > 0
2) S ближе к окружности, чем D Û
(xs)2 + (ys)2 +(xd)2 + (yd)2 - 2*R2 < 0
| ||
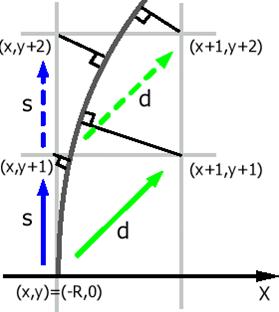 Рис. 4. Алгоритм Брезенхема.
Рис. 4. Алгоритм Брезенхема.
| Пусть (x,y) - текущий пиксел. Обозначим FS=f(x,y+1)= x2+(y+1)2 - R2 >0 Fd=f(x+1,y+1)= (x+1)2+(y+1)2 - R2 <0 F= FS+Fd DF(s) = (DFпри переходе s: (x,y)->(x,y+1)) = f(x,y+2)+ + f(x+1,y+2) - f(x,y+1) - f(x+1,y+1)=4y+6 DF(d) = (DFпри переходе d: (x,y)->(x+1,y+1)) = f(x+1,y+2) + f(x+2,y+2) - f(x,y+1) - f(x+1,y+1)=4x+4y+10 | ||
Тогда из двух возможных смещений d и s мы выберем:
1) F=FS+Fd > 0 Û FS > -Fd,т.е. (x+1,y+1) ближе к окружности,чем (x,y+1):
d: Переходим в (x+1,y+1) и придаем соответствующие приращения F, DF(s), DF(d)
F=F+DF(d); DF(s)=DF(s) +4; DF(d)=DF(d) + 8;
2) F=FS+Fd < 0 Û FS < -Fd,т.е. (x,y+1) ближе к окружности,чем (x+1,y+1):
s: Переходим в (x,y+1) и придаем соответствующие приращения F, DF(s), DF(d)
F=F+DF(s); DF(s)=DF(s) +4; DF(d)=DF(d) + 4;
Если мы начинаем из (-R,0), то начальные значение будут следующими:
F = FS + Fd = ((-R)2+12 - R2)+ ((-R+1)2+12 - R2) = 1+(-2*R+1+1)=3-2*R;
DF(s)=4*0+6=6;
DF(d)=4*(-R)+4*0+10=10 - 4*R;
Легко видеть, что в алгоритме все величины, связанные с F, кроме F начального, будут кратны 2. Но, если мы поделим все эти величины на 2 (в дальнейшем, значения всех величин уже понимаются в этом смысле), то Fнач = 1/2+1-R. Т.к. приращения F могут быть только целочисленными, то F=1/2+T, где TÎ Z; т.е. если отнять 1/2 от всех значений, то знак F не изменится для всех T, кроме T =0. Для того, чтобы результат сравнения остался прежним, будем считать, что F=0 теперь соответствует смещению s.
Алгоритм:
x=-r;
y=0;
F=1-r;
dFs=3; // DF(s)
dFd=5-2*r; // DF(d)
while (x+y <=0)
{
plot8 (x,y);
if(F>=0)
{
// d: Диагональное смещение
F+=dFd;
x++; y++;
dFs+=2;
dFd+=4;
}
else
{
// s: Вертикальное смещение
F+=dFs;
y++;
dFs+=2;
dFd+=2;
}
}
Размерность вычислений этого алгоритма (т.е. отношение максимальных модулей значений величин, с которыми он оперирует к модулям исходных данных (в данном случае R)) равна 2.
Алгоритм Кузьмина. [Kuzmin, 1990]
Быстрее, использует всего 3 переменные и имеет размерность вычислений 1. Данный алгоритм фактически является модификацией алгоритма Брезенхема и получен из него делением соответствующих переменных еще раз на 2, что привело к необходимости использовать понятие четности для определения точки старта. Подробнее смотри [Kuzmin, 1990].
Алгоритм:
x=R;
y=0;
e=-R/2;
if(R & 1) { e--; goto odd; }
even:
plot8(x,y);
if(y>=x) return;
e+=y++;
if(e>=0) e-=--x;
odd:
plot8(x,y);
if(y>=x) return;
e+=++y;
if(e>=0) e-=--x;
goto even;
 2014-02-24
2014-02-24 766
766








