Предел функции в точке

Лекция № 6

Список используемой литературы

Вопросы для самопроверки

1. Функция.

2. Область определения функции

3. Способы задания функции

4. Основные элементарные функции и их графики

1 Ухоботов, В. И. Математика: Учебное пособие.- Челябинск: Челяб. гос. ун-т, 2006.- 251 с.

2 Ермаков, В.И. Сборник задач по высшей математике. Учебное пособие. –М.: ИНФРА-М, 2006. – 575 с

3 Ермаков, В.И. Общий курс высшей математики. Учебник. –М.: ИНФРА-М, 2003. – 656 с.

Тема «Предел функции»

Цель: рассмотреть понятие предела функции, связь между бесконечно большими и бесконечно малыми функциями, основные теоремы о пределах, некоторые замечательные пределы.

Ключевые слова: предел, бесконечно малые, бесконечно большие функции, замечательные пределы.

Вопросы:

1. Предел функции в точке
2. Предел функции при стремлении аргумента к бесконечности
3. Основные теоремы о пределах
4. Бесконечно малые функции
5. Бесконечно большие функции и их связь с бесконечно малыми.
6. Сравнение бесконечно малых функций
7. Свойства эквивалентных бесконечно малых
8. Некоторые замечательные пределы
9. Решение примеров

y f(x)

A + e

A

A - e

0 a - D a a + D x

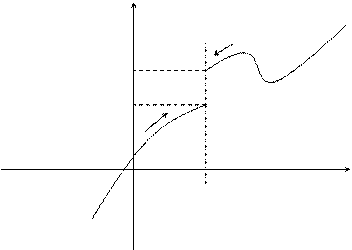
Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)

Определение. Число А называется пределом функции f(x) при х®а, если для любого e>0 существует такое число D>0, что для всех х таких, что

0 < ïx - aï < D

верно неравенство ïf(x) - Aï< e.

То же определение может быть записано в другом виде:

Если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.

Запись предела функции в точке: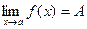

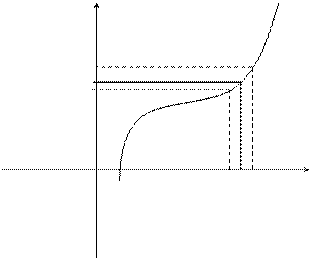
Определение. Если f(x) ® A₁ при х ® а только при x < a, то 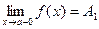- называется пределом функции f(x) в точке х = а слева, а если f(x) ® A₂ при х ® а только при x > a, то 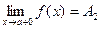называется пределом функции f(x) в точке х = а справа.

у

f(x)

А₂

А₁

0 a x

Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы А₁ и А₂ называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x).

2. Предел функции при стремлении аргумента к бесконечности.

Определение. Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство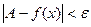

При этом предполагается, что функция f(x) определена в окрестности бесконечности.

Записывают: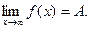

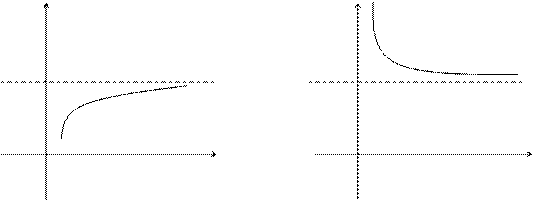
Графически можно представить:

y y

A A

0 0

x x

y y

A A

0 0

x x

Аналогично можно определить пределы 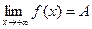для любого х>M и

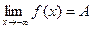для любого х<M.

3. Основные теоремы о пределах.

Теорема 1. 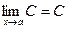, где С = const.

Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а.

Теорема 2.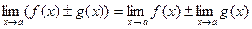

Теорема 3.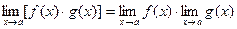

Следствие.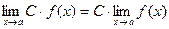

Теорема 4. 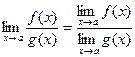при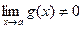

Теорема 5. Если f(x)>0 вблизи точки х = а и 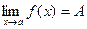, то А>0.

Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.

Теорема 6. Если g(x) £ f(x) £ u(x) вблизи точки х = а и 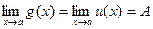, то и .

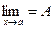Определение. Функция f(x) называется ограниченной вблизи точки х = а, если существует такое число М>0, что ïf(x)ï<M вблизи точки х = а.

Теорема 7. Если функция f(x) имеет конечный предел при х® а, то она ограничена вблизи точки х = а.