Раздел IV. ОСНОВЫ ГЕОДЕЗИЧЕСКИХ ВЫЧИСЛЕНИЙ
Рис. 3.2
Лист карты масштаба 1:10000 получается путем деления листа карты масштаба 1:25000 на четыре части, обозначаемые арабскими цифрами 1, 2, 3, 4, которые приписываются к номенклатуре карты 1:25000, например, N-37-49-А-б-2.
Лист карты масштаба 1:5000 получают путем деления листов карты масштаба 1:100000 на 256 частей. Номенклатура этих листов образуется прибавлением к номенклатуре листа 1:100000 номера в скобках соответствующего листа карты масштаба 1:5000, например N-37-49-(253).
Для разграфки листа карты масштаба 1:2000 лист карты масштаба 1:5000 делят на девять частей, обозначаемых строчными буквами русского алфавита от а до и, записываемыми в круглых скобках после цифры, обозначающей номер листа карты масштаба 1:5000, например, N-37-49-(253-д).
В табл. 3.2 показаны разграфка и номенклатура топографических карт.
Таблица 3.2
| Масштаб карты | Размер листа | Пример номенклатуры | |
| по широте | по долготе | ||
| 1:1000000 1:500000 1:200000 1:100000 1:50000 1:25000 1:10000 1:5000 1:2000 | 40 20 40¢ 20¢ 10¢ 2¢ 2¢30² 1¢15² 25² | 60 30 10 30¢ 15¢ 7¢30² 3¢45² 1¢52,5² 37,5² | N-37 N-37-Г N-37-VI N-37-49 N-37-49-А N-37-49-А-б N-37-49-А-б-2 N-37-49-(253) N-37-49-(253-д) |
При выполнении геодезических работ производят измерения углов, расстояний, площадей, превышений и т.п. Под измерением некоторой величины X понимают ее сравнение с эталонной величиной q, принятой за единицу меры. Результатом измерения величины является число l, показывающее во сколько раз единица измерения укладывается в измеряемой величине. В общем случае число l может быть целым, дробным, большим или меньшим единицы.
Определения величин могут быть непосредственными и косвенными. В первом случае производиться непосредственное сравнение измеряемой величины с единицей меры. Во втором – необходимую величину получают при помощи вычислений, проводимых по другим непосредственно измеренным величинам. Примером косвенных определений может служить вычисление гипотенузы прямоугольного треугольника по измеренным катетам.
Если измерение некоторой величины производится в однородной среде одним наблюдателем, одним и тем же прибором, в одинаковых условиях, то их называют равноточными измерениями. В противном случае измерения называют неравноточными.
В количественном отношении измерения подразделяются на необходимые и избыточные (добавочные). Например, если некоторый отрезок прямой линии на местности измерен n раз, то необходимым является одно измерение, остальные n -1 измерения – избыточные. Избыточные измерения служат средством контроля и позволяют судить о качестве измерений, а также позволяют определять с большей точностью искомую величину.
Результаты измерений всегда содержат некоторую погрешность. Под погрешностью d результата измерений l понимают разность:
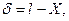
где X – точное значение измеренной величины.
Измерения, проводимые определенным прибором, не могут быть произведены с меньшей погрешностью, чем погрешность, обеспечиваемая измерительным прибором. Например, если измеряется расстояние мерным прибором (рулеткой), длина которого определена с погрешностью 0,1%, то нельзя получить конечный результат с погрешностью 0,01%.
На практике не следует производить измерения с наибольшей достижимой точностью, так как повышение точности измерений ведет к удорожанию измерительных приборов, поэтому точность измерений должна соответствовать поставленной задаче.
Погрешности, возникающие при измерениях, подразделяют на грубые, систематические и случайные.
При измерениях не должны появляться погрешности больше предела, установленного для данных условий. Однако иногда встречаются грубые погрешности, которые происходят от недостаточного внимания исполнителей при измерениях. Например, при измерении линии лентой имеют место случаи просчета лент, а при измерении углов – случаи просчета нескольких градусов или десятков минут. Грубые погрешности обнаруживают путем повторения измерения и сравнения их результатов. Если расхождения между результатами превосходят заданный допуск, то эти измерения выбраковывают и производят заново.
К систематическим погрешностям относят погрешности, вызываемые факторами, действующими одинаковым образом при нескольких повторных измерениях. Такие погрешности возникают в силу ряда причин: несовершенства приборов (инструментальные погрешности); действия внешних условий измерения (погрешности среды); действия личных качеств наблюдателя и др. При рациональной организации измерений (наблюдений) и технических усовершенствованиях систематические погрешности удается исключить или свести их до минимума.
К случайным погрешностям относятся все остальные погрешности, исключить которые не представляется возможным. Например, при отсчете по делениям линейки появляются случайные погрешности из-за неточности оценки на глаз долей интервалов между двумя штрихами линейки и др. Случайные погрешности носят такое название потому, что они в отдельных измерениях отличаются друг от друга, причем эти различия имеют случайный характер.
Точность проведенного измерения может быть оценена по абсолютной погрешности или по относительной погрешности. Например, при измерении углов удобной мерой точности является абсолютная величина погрешности, а при оценке измеренных расстояний более удобна относительная погрешность. Относительная погрешность d отн представляет собой отношение абсолютной величины погрешности d абс к измеряемой величине l, т.е.
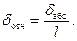
Относительная погрешность часто выражается в процентах:
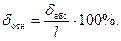
Рассмотрим два случая измерения расстояния: в первом – измерена линия длиной 100 м с абсолютной погрешностью 1 см и во втором – линия длиной 1000 м измерена с той же абсолютной погрешностью. Если судить по абсолютным погрешностям, то создается впечатление, что точности измерений одинаковы в обоих случаях. Если использовать относительные погрешности, то оказывается:
для первой длины
dотн = 1 см/10000 см = 1/10000;
для второй длины
dотн = 1 см/100000 см = 1/100000.
Таким образом, точность измерения во втором случае на порядок выше, чем в первом.
Случайные погрешности обладают четырьмя свойствами:
1) при измерениях равновероятно возникновение случайных погрешностей, равных по величине и противоположных по знаку;
2) малые по абсолютной величине случайные погрешности встречаются чаще, чем большие;
3) при данных условиях измерений случайные погрешности по абсолютной величине не могут превосходить известного предела;
4) среднее арифметическое из случайных погрешностей равноточных (одинаково точных) измерений стремится к нулю при неограниченном возрастании числа измерений.
 2014-02-09
2014-02-09 1229
1229
