Требования к математическим моделям, используемым при разработке метрологической службы предприятия

Место математических методов в метрологической системе (в системе метрологических процедур) предприятия

Все метрологические и квалиметрические процедуры, используемые на предприятиях и в организациях, в соответствии с международными стандартами ISO серии 9000 формируют систему менеджмента качества предприятий и организаций.

Формирование метрологической службы включает этапы:

-1. определяют перечень метрологических процедур, влияющих на результирующее качество работы организации или предприятия (качество выпускаемой продукции, предоставляемых услуг);

- 2.устанавливают последовательность этих процессов, их взаимное влияние, определяют обратные связи;

- 3. для каждого процесса формируется его обеспечение соответствующими материальными (сырьем, оборудованием, персоналом) и интеллектуальными (информацией, методическими материалами, программным обеспечением, методиками выполнения измерений, средствами измерений) ресурсами;

- 4. разрабатываются критерии оценки процессов и методы эффективного управления этими процессами; на окончательном этапе формируют критерии оценки и разрабатывают методики измерения, оценки, анализа всей совокупности процессов и их отдельных этапов.

Критериями классификации математических методов, используемых в рамках метрологической системы, могут быть цели применения того или много метода, место математического метода в метрологической системе, такие особенности применения метода, как возможность использования сложных аналитических зависимостей, удобство и простота, универсальность или специфика метода и т.д.

Очевидно, что при формировании и разработке метрологической системы предприятия наиболее эффективным математическим методом является математическое моделирование [60,61], т.е. процесс замещения объекта исследования некоторой его моделью и проведение исследований на модели с целью получения информации об объекте.

При функционировании уже разработанной метрологической службы необходимо использовать математические методы, позволяющие оценивать точность проводимых измерительных и контрольных процедур, стабильность точностных параметров средств и методов измерений; позволяющие оценивать эффективность проводимых изменений в технологических процессах, в системе управления, а также методики, позволяющие обнаруживать и устранять дефекты, реагировать на требования рынка, на рекламации потребителей, оценивать результативность проводимых мероприятий [60-64].

При разработке структуры процессов, составляющих метрологическую систему предприятия, можно использовать различные математические модели:

Выбор зависит от:

- 1. степени детализации анализируемой системы (декомпозиции);

- 2. уровня иерархии анализа (обобщенный или подробный анализ отдельных процессов, чем ниже уровень анализа, тем более подробной и детальной должна быть используемая математическая модель);

- 3. этапа разработки (предварительный, промежуточный, заключительный).

Разнородность кинематографических предприятий и организаций, очевидно, не способствуют разработке однотипных универсальных методов построения математических моделей, описывающих метрологические и квалиметрические системы.

Тем не менее, следует сформулировать общие требования к этим моделям:

1. Адекватность - способность отражать исследуемые свойства с необходимой точностью. Погрешность модели Е по всей совокупности m исследуемых выходных параметров системы может быть оценена как

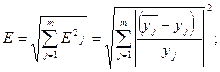
где Е_j - относительная погрешность модели по j -му параметру;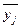- значение j -го параметра, определенного с помощью математической модели, у_j - значение этого же параметра, полученное экспериментально либо определенное с помощью более точной математической модели.

2. Объективность - соответствие выводов, сделанных с помощью модели, реальным условиям. Называя это свойство, необходимо иметь в виду, что никакая модель не может адекватно отражать свойства реальных процессов и объектов, необходимо учитывать предварительные условия, предположения, ограничения и т.д.

3.Простота – незасоренность модели малозначащими факторами. Стремление к простоте модели продиктовано, прежде всего, ограниченными возможностями вычислительной техники, стремлением получить практические результаты при решении сложных и неоднозначных задач и т.д.

4.Чувствительность– способность модели реагировать на изменение исходных условий (начальных параметров). 5.Устойчивость- способность модели выдавать стабильные выходные характеристики при незначительном (предельно допустимом) изменении влияющих факторов.

Требования чувствительности и устойчивости отражают объективные характеристики производственных и внепроизводственных процессов.

6.Универсальность– возможность использования данной модели для различных условий и применительно к различным объектам.

Следует отметить, что перечисленные свойства противоречат друг другу. При выборе конкретной модели необходимо выделить более важные и пренебречь незначительными. Для того чтобы математическая модель удовлетворяла приведенным требованиям, ее разработка должна проводится после предварительного изучения предметной области, которую эта модель описывает.

Только в результате предварительного изучения предметной области (метрологической системы предприятия или организации, измерительная процедура, измерительного прибора) можно отличить цели от средств их достижения, следствия от причин, основные факторы от второстепенных и т.д.