Кластерный анализ. Кластерный анализ позволяет проводить классификацию измеряемых объектов на группы, классы, кластеры одновременно по всем наиболее существенным признакам

Кластерный анализ позволяет проводить классификацию измеряемых объектов на группы, классы, кластеры одновременно по всем наиболее существенным признакам. Термин впервые ввел Tryon в 1939 г., в дальнейшем его развил Hartigan [76].

В отличие от метода группировок, в котором сначала выделяются группы объектов с определенными признаками, а затем проводится классификация по признакам, кластерный анализ предполагает определение количественных критериев по комплексу признаков и теоретическое обоснование качественного отличия выделенных групп объектов.

К достоинствам метода следует отнести формулирование единой количественной меры для всех признаков и чисто количественное определение границ групп объектов.

Можно сформулировать алгоритм проведения кластерного анализа.

1.Исходные данные:

- измеряемые объекты (1,…, j,…,m),

- каждый объект характеризуется 1, …,i,…,k признаками,

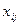- - значение i –го признака у j -го объекта.

Объекты необходимо классифицировать по совокупности характеристик.

2. Поскольку характеристики могут иметь различную размерность, их нормируют:, т.е. находят их относительные нормированные отклонения от средних значений (отклонения i -ой характеристики для j -го объекта относительно среднего значения i -ой характеристики для всех объектов)

,

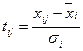где 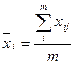- среднее значение характеристики для всех объектов;

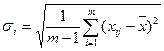- среднеквадратическое отклонение характеристики для объектов.

3.Определяется какая-либо функция расстояния между кластерами (объектами), показывающая, насколько j -ый объект удален по i- му признаку относительно j +1 –го объекта,

Используются следующие функции расстояния:

- евклидово расстояние ,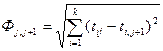

- функция расстояния, учитывающая весомость каждого отдельного признака, характеризуемую коэффициентом весомости 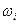, который может быть определен на основании результатов экспертного опроса, корреляционно- регрессионного анализа, факторного анализа и т.п., то .

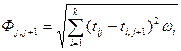- квадрат евклидова расстояния, когда хотят придать больший вес удаленным объектам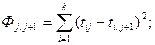

- «расстоянием городских кварталов» (манхэттенским расстоянием), соответствующим среднему значению разностей координат, в меньшей степени учитывающему большие отклонения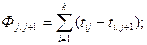

- расстоянием Чебышева ;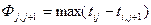

- степенным расстоянием 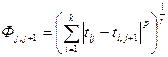, в котором p – коэффициент, учитывающий вес отдельных параметров; r – значимость больших отклонений между объектами; при p=r=2 функция становится евклидовым расстоянием и т.д.!!!

4.Выбор количества кластеров.

Количество кластеров может быть известно заранее или нет.

Если количество кластеров известно заранее:

устанавливаются типичные представители кластеров и по ним определяют значения характеристик. Остальные объекты относят к тому из классов, с которым они имеют минимальную функцию расстояния.

Если количество кластеров заранее неизвестно, это количество определяется методом перебора, используя пороговое расстояние.

Для этого сначала определяется функция расстояния для пар объектов. Устанавливается пороговое значение функции расстояния. Объединяют в кластеры такие объекты, расстояние между которыми меньше порогового расстояния. При этом получают определенное количество кластеров, но некоторые объекты в них не входят. Центры тяжести сформированных кластеров считают реперными точками на измерительной оси. Расстояния между этими точками сравнивают с расстояниями между объектами, затем меняют пороговые значения, чтобы все объекты вошли в определенные кластеры. Процесс объединения заканчивают, когда все функции расстояния становятся меньше пороговых значений. Можно без изменения пороговых значений расстояний объединить в один кластер объекты, имеющие минимальные функции расстояния.