Основные операции над отношениями

Способы задания отношений.

Пара элементов a и b отношения обозначается (а, b), где a — первый, b — второй элемент пары. Если а 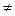b, то (а, b) 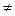(b, а) — такая пара называется упорядоченной. Отношения обычно обозначают греческими буквами 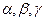и т. д. Если а и b находятся в отношении 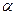, то записывают (а, b) 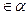или а 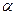b. Отношения можно задать тремя способами:

1. Бинарные отношения можно задать перечислением пар элементов, находящихся в рассматриваемом отношении

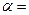{(a₁, b₁),..., (a_n, b_n)}

2. Отношения можно задать графически или аналитически

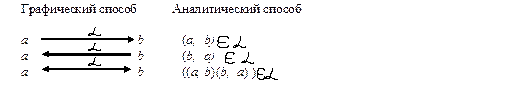
3. Матричный способ задания отношения

Пусть имеются два множества элементов А и В. Пусть m, n — мощности этих множеств (количество элементов в них). Запишем таблицу С размером mxn, в которой строки соответствуют элементам множества А, столбцы — элементам множества В.

Пусть в этой таблице элементы Сij=1, если аi 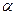bj;

Cij=0, если аi, bj не находятся в отношении .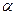

Такая таблица, состоящая из 0 и 1, называется булевой матрицей отношений.

Пример:

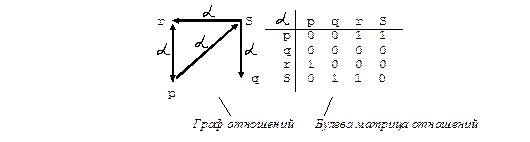
Бинарные отношения — это множества пар элементов, связанных этими отношениями, поэтому к отношениям применимы все операции, выполняемые над множествами:

· обьединение;

· пересечение;

· равенство;

· включение;

· дополнение.

Пусть 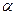и 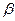два разных отношения, тогда:

1. Включение 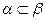обозначает, что все пары (а, b), находящиеся в отношении 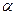, находятся также в отношении 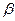, но не наоборот

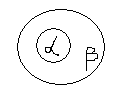
Пример: если 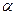- отношение доминирования,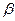- отношение предпочтения, то все пары элементов (а, b), находящиеся в отношении доминирования, находятся также и в отношении предпочтения, но не наоборот.

2. Равенство 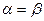означает, что эти отношения состоят из одних и тех же упорядоченных пар.

Пример: если 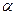- отношение равенства первого элемента пары второму, 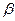- отношение равенства второго элемента пары первому, то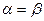

3. Пересечение 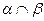— это множество упорядоченных пар, одновременно принадлежащих отношениям 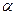и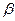

Пример: если 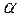- отношение доминирования или безразличия между первым элементом пары и вторым, а

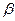- отношение доминирования или безразличия между вторым элементом пары и первым, то, 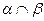- это множество пар, находящихся в отношении безразличия.

4. Объединение 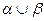— это множество упорядоченных пар, принадлежащих хотя бы одному 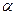или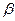

Пример: если 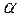- отношение безразличия, 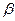- отношение доминирования, то все пары элементов (а, b), находящиеся в отношении сравнения, находятся либо в отношении доминирования, либо в отношении безразличия. Все эти пары принадлежат объединению 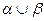указанных отношений.

5. Разность 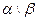— это множество пар, принадлежащих множеству 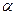, но не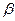

Пример: в предыдущем примере пары, в которых первый элемент только доминирует над вторым, но не находится с ним в отношении безразличия, находятся в отношении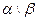

Операции обьединения, пересечения отношений и другие могут относиться не только к двум отношениям, но и к их группам.