Определение условий эффективного производства
Функция производства может быть разбита на три стадии.
Стадия 1 начинается с 0 и заканчивается в точке, в которой средний продукт (АРv) по переменному ресурсу максимален.
Стадия 2 начинается с АРv мах. до точки, в которой выработка максимальная, МР = 0.
Стадия 3 начинается с точки, когда совокупная выработка начинает падать, а предельный продукт МР меньше 0.
На сколько эффективно используются ресурсы на этих стадиях? Эффективность ресурса лучше всего измерять средним продуктом по ресурсу, так как он показывает количество выработки на единицу ресурса.
Так как на стадии 1 средний продукт по переменному ресурсу растет. То ясно. Что этот ресурс используется с увеличивающейся эффективностью. Максимальная эффективность переменного ресурса достигается на границе 1-ой и 2-ой стадий, где АР максимален.
Так как общая выработка растет до границы 2-ой и 3-ей стадий, то эффективность постоянного ресурса достигается на границе стадий 2 и 3.
При возрастании эффективности постоянного и переменного ресурсов себестоимость единицы продукции падает. Иными словами, с точки зрения повышения эффективности производства и снижения издержек на единицу продукции фирме следует пройти стадии 1, по крайней мере до границы со стадией 2, прежде чем прекратить увеличивать использование переменного ресурса..
На стадии 2 рост выработки замедляется. На стадии 2 происходит падение среднего продукта по переменному ресурсу. Однако средний продукт по постоянному ресурсу продолжает возрастать, так как продолжает возрастать выработка.
На стадии 3 снижается АРv, а МР становится отрицательным. При снижении общей выработки снижается также АРf по постоянному ресурсу. Иными словами после перехода границы стадии 3 снижается эффективность использования как постоянного, так и переменного ресурсов.
Таким образом, оптимальная эффективность производства всегда находится в пределах стадии 2.
Для определения точки стадии 2, в которой ресурсы используются максимально эффективно, а себестоимость продукции минимальна, следует рассмотреть стоимость ресурсов.
Рассмотрим комбинацию 2-х видов ресурсов – труда (L) – переменного и капитала (С) – постоянного (рис).
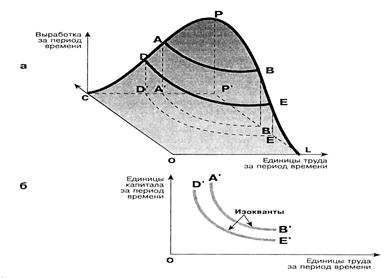 |
Изменения капитала и труда дают поверхность производства СДАР. При С = const изменение количества труда L дают функцию производства СДАР. При L = const изменение количества капитала дает функцию LЕВР.
Соединим все точки поверхности производства соответствующие выработке АА¢ (АА¢ =ВВ¢) и получим контурную линию АВ, проекция которой на горизонтальную плоскость даст линию А¢ В¢. При выработке ДД¢ получим проекцию Д¢Е¢. Этим линии называются изоквантами, которые представляют собой все комбинации ресурсов, позволяющие достичь данного объема выработки. Они показаны на рисунке.
Изокванте А¢ В¢ соответствует большая выработка, чем изокванте Д¢ Е¢, т.е. она находится дальше от начала координат. Весь набор изоквант называется картой изоквант.
Один и тот же объем производства можно получить при различном сочетании факторов производства. Это положение базируется на действии принципа замещения. Обратимся к рисунку.
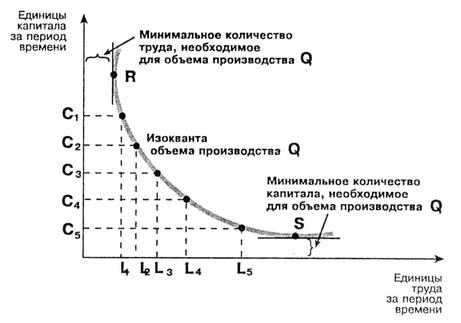 |
Степень замены капитала трудом (при Q = const) называется предельной степенью технического замещения капитала (MRTS)
MRTS = С2 – С1 / L2 –L1 = - D C/ D L
“Потеря” выработки от сокращения затрат капитала в точности возмещается «прибавкой» выработки за счет увеличения затрат труда.
Потеря выработки от снижения затрат капитала равна
DQc = -DC*MPc
Прибавка выработки от увеличения затрат труда
DQc =DL*MPl
или
-DC*MPc = DL*MPl
MRTS = - D C/ D L = МРl / МРс
D C/ D L характеризует наклон касательной. Следвательно, в любой точке изокванты предельная степень технического замещения одного ресурса другим равна наклону касательной к изокванте в этой точке.
Как следует из приведенного рисунка один ресурс заменяется другим в прогрессивных количествах
C1С2= С2С3 = С3С4 = С4С5
L1L2= L2L3 = L3L4 = L3L5
Оптимальная комбинация ресурсов должна определяться с учетом стоимости этих ресурсов.
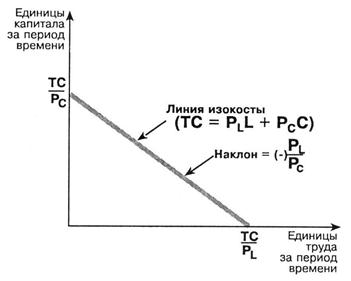
Кривая изокосты показывает альтернативные комбинации ресурсов, которые фирма может купить с учетом действующих цен и своего бюджета (ТС).
Обозначим через Рl цену труда, а через Рс цену капитала. Расходы фирмы на труд составят Рl*L; расходы на капитал Рl*C. Тогда
ТС = Рl *L + Рс*С
При бюджете ТС и цен на капитал Рс максимальное количество капитала составит ТС/Рс; аналогично, если использовать все деньги на труд, то фирма сможет приобрести ТС/L единиц труда.
 |
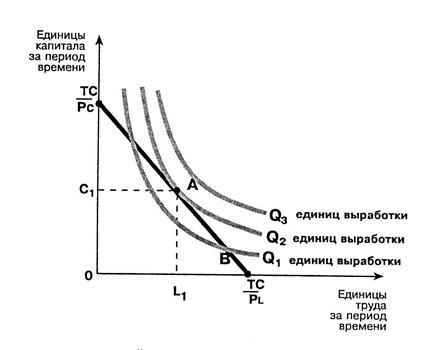 |
Цель повышения эффективности производства состоит в том, чтобы получить максимальную выработку от данного количества используемых ресурсов. На языке анализа изокванты-изокосты это означает достижение максимально высокой кривой изокванты (рис.)
Точка касания изокванты и изокосты определяет оптимальную комбинацию ресурсов при максимальной выработке при данных совокупных затратах на ресурсы и данных ценах. При комбинации C1 и L1 обеспечивается минимальные издержки по ресурсам.
В точке касания изокосты и максимально достижимой изокванты наклон линии изокосты равен наклону изокванты:
наклон изокванты = (-) МРl / МРc
наклон изокосты = (-) Рl / Рс или
(-) МРl / МРс = Рl /Рс
Откуда
МРс/Рс = МРl /Рl
Таким образом, оптимизация ресурсов для любой пары ресурсов требует равенства между предельной степенью технического замещения и соотношением цен этих ресурсов.
Производство, эффективное по издержкам, требует, чтобы фирма так распределяла средства на приобретение ресурсов, чтобы получить одинаковые количества дополнительной выработки от последней денежной единицы, затраченной на каждый ресурс.
Эти выводы справедливы, если используются более двух ресурсов. При использовании ресурсов Ха,Хв,Хс,…Х n и ценах Рха,Рхв,Рхс,…Рхn
Рха*Ха + Рхв*Хв + Рхс*Хс +…+ Рх n*Хn =ТС
Мрха/Рх = МРхв/Рхв =МРхс/Рс = … =МРхn/Рхn
IВопросы к теме:
1. Раскройте содержание термина «функция производства»
2. Что показывает краткосрочная функция производства?
3. Что показывает предельный и средний продукт по переменному и постоянному ресурсам?
4. На какой стадии функции производства обеспечивается оптимальная эффективность использования переменного ресурса?
5. Что представляют собой изокванты?
6. Как определяется предельная степень технического замещения капитала?
7. Что показывает кривая изокосты?
8. Сформулируйте правило оптимального сочетания ресурсов.
 2014-02-24
2014-02-24 775
775








