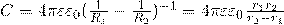
Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:
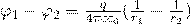
Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:
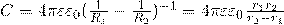
При малой величине зазора, то есть  , а следовательно можно считать, что
, а следовательно можно считать, что 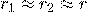 емкость сферического конденсатора будет равна
емкость сферического конденсатора будет равна 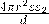 . Площадь сферы
. Площадь сферы  следовательно формула будет совпадать с формулой емкости плоского конденсатора
следовательно формула будет совпадать с формулой емкости плоского конденсатора 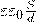
Так же есть:
Энергия конденсатора: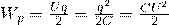
Ёмкость конденсатора: 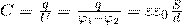
Ёмкость цилиндрического конденсатора: 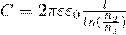
Емкость плоского конденсатора: 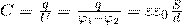 ;
;
В Формуле мы использовали:
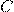 — Электроемкость сферического конденсатора
— Электроемкость сферического конденсатора
 — Относительная диэлектрическая проницаемость
— Относительная диэлектрическая проницаемость
|
|
|
 - Электрическая постоянная
- Электрическая постоянная
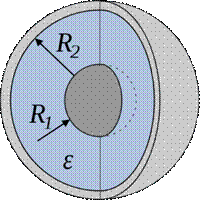
 — Больший радиус (от центра, до края конденсатора)
— Больший радиус (от центра, до края конденсатора)
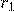 — Малый радиус (Его может и не быть — это пустота)
— Малый радиус (Его может и не быть — это пустота)
Ёмкость цилиндрического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.
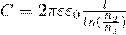
Для определения емкости цилиндрического конденсатора, который состоит из двух полых коаксиальных цилиндров с радиусами r1 и r2 (r2 > r1), один вставлен в другой, считаем поле радиально-симметричным и действующим только между цилиндрическими обкладками, так же пренебрегаем краевыми эффектами. Разность потенциалов между обкладками считаем по формуле для разности потенциалов поля равномерно заряженного бесконечного цилиндра с линейной плотностью τ =Q/l. При наличии диэлектрика между обкладками разность потенциалов
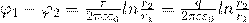
Подставим в формулу электроемкости конденсатора и у нас получится формула для цилиндрического конденсатора:
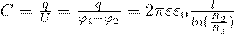
Так же есть:
Энергия цилиндрического конденсатора: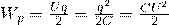
Ёмкость конденсатора: 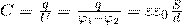
Ёмкость плоского конденсатора: 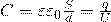
Емкость сферического конденсатора: 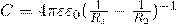
В формуле мы использовали:
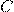 — Ёмкость цилиндрического конденсатора
— Ёмкость цилиндрического конденсатора
 — Линейная плотность
— Линейная плотность
 — Относительная диэлектрическая проницаемость
— Относительная диэлектрическая проницаемость
 - Электрическая постоянная
- Электрическая постоянная
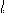 — Длина цилиндрического конденсатора
— Длина цилиндрического конденсатора
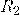 — Больший радиус (от центра, до края конденсатора)
— Больший радиус (от центра, до края конденсатора)
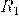 — Малый радиус (Его может и не быть — это пустота)
— Малый радиус (Его может и не быть — это пустота)
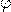 — Потенциал проводника
— Потенциал проводника
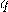 — Точечный заряд
— Точечный заряд
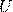 — Напряжение
— Напряжение
 2014-02-24
2014-02-24 4041
4041








