2014-02-24
1620
Однородно намагниченное тело:
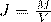
Любое вещество, помещенное в магнитное поле, приобретает некоторый магнитный момент. Намагниченность J – это магнитный момент единицы объема.
В несильных полях намагниченность прямо пропорциональна напряженности поля, вызывающего намагничивание::
Если же тело намагничено неоднородно (состоит из нескольких частей), то намагниченность определяется для каждого физически малого объема dV
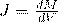
Намагниченность тел зависит от внешнего магнитного поля и температуры. У ферромагнетиков зависимость J от напряженности внешнего поля Н выражается кривой намагничивания. В изотропных веществах направление J совпадает с направлением Н, в анизотропных направления J и Н в общем случае не совпадают.
Единица измерения намагниченности в Международной системе единиц — ампер на метр (1 А/м — это такая намагниченность, при которой 1 м3 вещества обладает магнитным моментом 1 Ам2)
В формуле мы использовали:
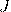— Намагниченность магнетика
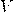— Объем тела
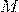— Магнитный момент тела
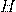— Магнитная восприимчивость вещества
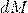— Магнитный момент в объеме тела dV
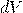— Маленькая часть объема
Первый закон Кирхгофа — Алгебраическая сумма токов, сходящихся в узле, равна нулю.
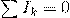
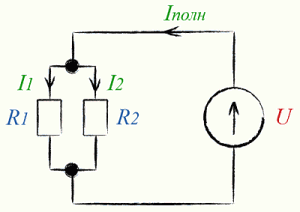
Первый закон Кирхгофа оперирует понятием узел. Узлом называется точка, в которой сходится более чем два проводника. Ток, текущий к узлу, считается положительным, текущий от узла имеет противоположный знак.
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов.
На нашем рисунке два узла, следовательно уравнений будет всего одно. Суммарный ток мы определим, используя первый закон Кирхгофа:
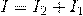
Давайте решим более сложную задачу на первое правило Кирхгофа.
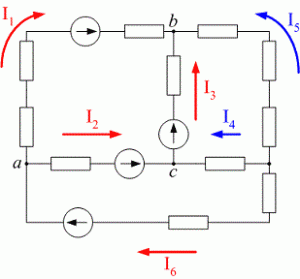
В данной схеме у нас четыре узла, следовательно у нас будет всего три уравнения.
Первый узел (а):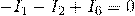 
Второй узел (b):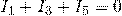 
Третий узел (c):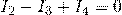 
Зная некоторые токи, с помощью данного закона, мы можем найти остальные (неизвестные) токи.
В формуле мы использовали:
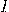— Ток в цепи
Плотностью потока энергии — средняя по времени энергия, которую электромагнитная или звуковая волна переносит в единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны
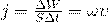
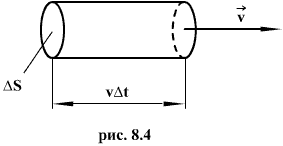
Через площадку S за время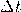 
будет перенесена энергия 
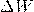заключенная в цилиндре с основанием S и высотой 
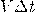. Если размеры цилиндра достаточно малы (за счет малости S и 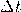) для того, чтобы плотность энергии во всех точках цилиндра можно было считать одинаковой, то можно найти как произведение плотности энергии w на объем цилиндра, S и 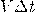и тогда получается, что энергия равна:
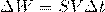
Подставим данную энергию в первоначальное уравнение и у нас получится:
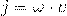
В Формуле мы использовали:
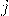— Интенсивность электромагнитной волны (плотностью потока энергии)
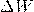— Энергия волны
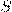— Площадь поверхности
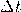— Время
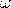— Плотность энергии
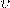— Скорость волны
