Закон Ома в дифференциальной форме — физический закон, определяющий связь между Электродвижущей силой источника или напряжением с силой тока и сопротивлением проводника

Закон Ома — сила тока в электрической цепи будет прямо пропорциональна напряжению приложенному к этой цепи, и обратно пропорциональна сумме внутреннего сопротивления источника электропитания и общему сопротивлению всей цепи.

Закон Ома для полной цепи — физический закон, определяющий связь между Электродвижущей силой источника или напряжением с силой тока и сопротивлением проводника.

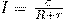
Из закона Ома для полной цепи вытекают следующие следствия:

Следствие 1: При r < < R Сила тока в цепи обратно пропорциональна её сопротивлению. А сам источник в ряде случаев может быть назван источником напряжения

Следствие 2: При r > > R Сила тока от свойств внешней цепи (от величины нагрузки) не зависит. И источник может быть назван источником тока.

Электродвижущая сила в замкнутой цепи, по которой течёт ток равняется:

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

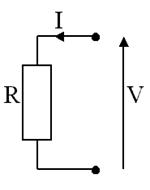
Так же изучите:

Закон Ома в дифференциальной форме: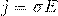

Закон Ома для переменного тока:

В Формуле мы использовали:

— ЭДС источника напряжения

— Внутреннее сопротивление источника напряжения

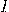— Сила тока в цепи

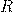— Сопротивление

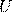— Напряжение в цепи

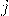— Вектор плотности тока

— Удельная проводимость

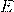— Вектор напряжённости электрического поля

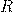— Сопротивление

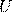— Напряжение в цепи

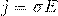
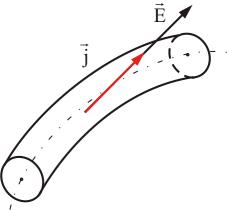
Вывод формулы Закона Ома в дифференциальной форме

Предположим, что напряженность поля не изменяется. Тогда под действием поля электрон получит постоянное ускорение равное

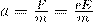
К концу пробега скорость упорядоченного движения достигнет значения

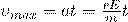
Тут t — среднее время между двумя последовательными соударениями электрона с ионами решетки. Друде не учитывал распределение электронов по скоростям и приписывал всем электронам одинаковое значение средней скорости. В этом приближении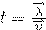

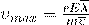
Скорость изменяется за время пробега линейно. Поэтому ее среднее (за пробег) значение равно половине максимального

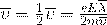
Полученную формулу подставим в

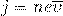
И у нас получилось

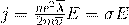
В Формуле мы использовали:

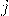— Вектор плотности тока

— Удельная проводимость

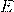— Вектор напряжённости электрического поля

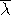— среднее значение длины свободного пробега

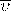— скорость теплового движения электронов

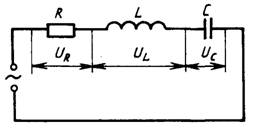
Закон Ома для переменного тока — Если ток является синусоидальным с циклической частотой ω, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается

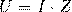
Полное сопротивление: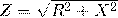

Сила переменного тока определяется при заданном напряжении не только сопротивлением R, которым обладает данная цепь при постоянном токе, но и наличием в этой цепи конденсаторов или катушек индуктивности. Поэтому, величины R и Z различны, т. е. одна и та же цепь будет иметь различное сопротивление для постоянного и для переменного тока.

В Формуле мы использовали:

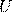— Напряжение (разность потенциалов)

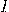— Сила тока

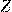— Полное сопротивление

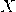— Реактивное сопротивление

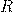— Активное сопротивление

Индуцированным магнитный момент

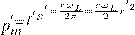
Среднее значение индуцированного магнитного момента

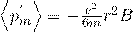
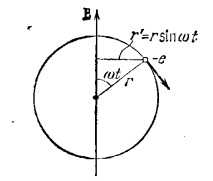
Тут мы использовали:

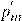— Индуцированным магнитный момент

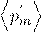— Среднее значение индуцированного магнитного момента

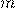— Масса электрона

— Заряд электрона

— Радиус орбиты

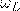— Ларморовая частота

Коэрцитивная сила — Это такое значение магнитного поля напряженностью H, которое необходимо приложить к ферромагнетику, предварительно намагниченному до насыщения, чтобы довести до нуля его намагниченность или индукцию магнитного поля

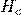— Коэрцитивная сила

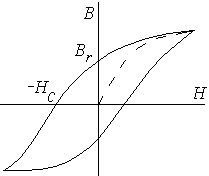
По величине коэрцитивной силы 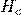магнитные материалы разделяются на магнитомягкие 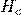и магнитотвердые 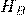. Граница этого раздела условная.

Величина коэрцитивной силы определяется механизмом перемагничивания и является структурно-чувствительной характеристикой материала. На 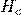влияют суммарная удельная поверхность зерен, остаточные механические напряжения, дефектность материала. Чем больше дефектность материала и меньше однородность структуры, тем больше Коэрцитивная сила 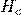, и соответственно меньше магнитная проницаемость. Это связано с тем, что наличие в образцах различных примесей, дефектов кристаллической решетки — все это затрудняет движению границ магнитных доменов.

Ларморова частота — угловая частота прецессии магнитного момента, помещенного в магнитное поле.

В формуле Ларморова частота учитывается то магнитное поле, которое действует на месте нахождения частицы. Это магнитное поле состоит из внешнего магнитного поля B и других магнитных полей, которые возникают из-за электронной оболочки или химического окружения.

В формуле мы использовали:

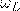— Ларморова частота

— Заряд электрона

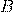— Вектор магнитной индукции

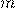— Масса электрона