ЗАТВЕРДЖУЮ
Оо
Оо
Оо оо
Оо оо
Оо
Оо
Оо
Оо оо
Оо
Оо
Оо
Оо
Y x
ИЗ
Dy
| y 3 |
x 7 · dx.
3. Возьмем неопределенные интегралы от обеих частей:
или
/ y~'^ dy = x^ • dx.
в результате вычисления этих интегралов получается соотношение
представляющее собой общи - нтеграл.
4. Из этого соотношения выразим y через x и C:
- 2 x C
y
| x 8 |
2 1
 + C 1
+ C 1
Эту формулу записываем в ответ. П
Задача 62. Найдите общее решение дифференциального уравнения
y (1 + x)dx + x(1 - y2)dy = 0.
Решение. 2. Это уравнение уже записано в терминах дифференциалов. Поэтому сразу разделим неременные, т. е. все, что содержит y и dy, перенесем в одну сторону, а все, что содержит x и dx, — в другую (в этом месте предполагается, что y = 0] очевидно, y (x) = 0 является решением):
1 - y 2 1 + x
dy = dx.
3. Возьмем пеонределенные интегралы от обеих частей:
/ dy = - dx.
y x
Вычислим эти интегралы:
/ -------- dy = - ------ dx,
y J x
I - dy - I ydy = - I — dx - I dx,
y x
ln\y\ - — = - ln \x\ - x + C.
Это — общий интеграл.
4. Из него выразить y через x невозможно. Поэтому в ответ запи
сываем формулу ln |y|- 2 = - ln |x|-x + C и специальное решение
y(x) = 0. П
10.5 Однородные дифференциальные уравнения
{Нелинейным) однородным, дифференциальным уравнением называют дифференциальное уравнение вида
y = f x
и нриводягциеся к нему.
Однородное дифференциальное уравнение с помощью замены
y (x)
| x |
z (x)
сводится, к уравнению с разделяющимися, перем,енным,и,. При этом используют формулы:
y (x) = x · z (x),
y'(x) = z(x) + x · z'(x),
dy = z (x) dx + x dz.
Замена неизвестной функции в общем виде выглядит так:
z(x) + x · z'(x) = f(z), z + xz' = f(z), xz' = f(z) - z, dz
dz
dx
Таким образом, для z(x) неременными
| f(z)-z
y(x)
= | x lacTC |
| dz | dx. x |
| = f (z) - z |
Отличительным свойством однородных уравнений является следующее. Если переменным x и y иринисать некоторую размерность (например, рубли), то правая часть уравнения окажется безразмерной.
Задача 63. Решите дифферепциальиое уравпепие
(x + 2y) dx — xdy = 0.
Решение. Это однородное дифференциальное уравнение. Поэтому сделаем замену z = f, используя формулы y = xz, dy = zdx + xdz. После замены получаем
(x + 2xz)dx — x(z dx + x dz) = 0.
Сократим на x:
dx + 2z dx — z dx — x dz = 0.
Или
dx + zdx — xdz = 0.
Получилось уравнение с разделяющимися перемеппыми. Решаем его но стандартной схеме:
(1 + z) dx — x dz = 0,
dx dz
x 1 + z, f dx f dz
x 1 + z
ln |x|+ C = ln | 1 + z|.
В конце возвращаемся к старой неизвестной функции:
y
| 1+ x |
ln |x| + C = ln
10.6 Линейные дифференциальные уравнения
Линейным дифференциальным уравнением (первого порядка) называют уравнение
y' = a (x)y + f(x)
а также его частный случай
y' = a (x)y.
Последнее уравнение называют линейным, однородным.^ оно может быть решено методом разделения переменных.
Теорема 55. Общее решение уравнения (10.2) имеет вид
y ор(x) = eA (x) e-A ( x)f(x)dx,
где A — любая первообразная функции a:
/ a (x) dx = A (x) + C.
В этой теореме индекс ор У функции yор является сокращением слов "общее решение".
Задача 64. Найдите общее решение линейного дифференциального уравнения
y' + 2y = e 3 x.
Решение. Решение будем искать в соответствии с теоремой 55. Запишем уравнение в нормальном виде:
| 3 x |
y
2 y + e
Из этой записи видно, что a(x) = - 2, а f(x) = e 3 x. Сначала найдем A. Имеем
| a (x) dx |
2 dx = - 2 x + C = A (x) + C.
Из этой формулы видим, что в качестве A можно взять функцию
A(x) = -2x. Далее находим решение но формуле из теоремы 55:
y ор(x) = eA (x) (e-A ( x ) f(x)dx =
| 2 x 2 x 3 x |
| 2 x 5 x |
e- e 2 x e 3 x dx = e- 2 x e 5 x dx
2x 1 e 5 x + C\= 1 e 3 x + Ce- 2 x.
Итак, в ответ записываем: yор(x) = 1 5 e 3 x + Ce 2 x.
Задача 65. Найдите общее решение линейного дифференциального уравнения
(1 + x2)y' = 2xy + (1 + x2)2.
Решение. Решение будем искать в соответствии с теоремой 55.
Чтобы понять, какие здесь a и f, перепишем уравнение в нормальном виде:
1 + x 2
Из этой записи видно, что a(x) = 1 + 2 ^f, а f(x) = 1 + x 2.
Правило: a — то, что умножается на y, а f — то, что ни на что не умножается (свободный член).
Сначала найдем A. Имеем
f f 2 x f dx
a(x) dx =----------- dx
1 + x 2 1 + x 2
= {z = x 2 }= f 1+ z = ln(1 + z) + C =
= ln(1 + x2) + C= A(x) + C. Из этой формулы видим, что в качестве A можно взять функцию
A(x) = ln(1 + x 2). Далее находим решение по формуле:
yо^(x)=e'' ( ^) j e-'' ( ^ ) f(x)dx =
= e ln(1+^^) I e - ln (1 + ^" (1 + x 2) dx =
= (1 + x2) /---------- (1 + x2) dx =
J 1 + x 2
= (1 + x2)(x + C).
Otbf.T: yо^(x) = (1 +x2)(x + C). и
10.7 Как определить тип дифференциального уравнения
Чтобы решить дифференциальное уравнение, совершенно необходимо правильно определить его тип, поскольку разные типы дифференциальных уравнений решаются разными методами. Решение любого дифференциального уравнения начинается с определения его типа. В нашей программе изучаются три типа дифференциальных уравнений.
1. Дифференциальное уравнение с разделяющимися пере.менны.ми при
водится к виду
y' = f(x) ■ g (y)
или
fi(x) • gi(y) dy = f 2(x) • g2 (y) dx.
Его характерная особенность: правая и левая часть представляют собой произведение функции, зависящей только от x, на функцию, зависящую только от y.
2. Однородное дифференциальное уравнение приводится к виду
Его характерная особенность: если x м y приписать какую-либо размерность, например, метры, секунды, рубли, то размерность должна сократиться.
3. Линейное дифференциальное уравнение приводится к виду
y' = a(x)y + f(x).
Его характерная особенность: y входит в уравнение только в первой степени.
Задача бб. Определите тип дифференциальных уравнений:
e 5 dy =dx,
x
(x 2 + 2xy) dy = (x 2 - y 2) dx, (x2 - 1) y ' + 2xy 2 = 0 .
Глава 11
Числовые ряды
11.1 Основные определения
Числовой ряд или просто ряд — это сумма бесконечного числа слагаемых или, аккуратнее, бесконечная последовательность чисел, соеди-пеппых знаками +:
^ un = u 1 + u 2 + ------------- +
n =1
Например,
^11111
n =1
^ 1 = 1 1 1 1
n=0
^(- 1) n = - 1 + 1 - 1 + 1 - 1 +
n =1
Пусть дай числовой ряд
оо n =1
Числа
n
Sn = u 1 + u2 + --------------------- un = ^uk
k=1
называют частичными суммами числового ряда. Они образуют последовательность.
Сум.мой числового ряда называют предел lim sn последовательности sn- Если ОН равен S, т. е.
lim sn = S,
| оо n=1 |
n
то пишут
Если lim sn существует (и конечен), то ряд называют сходящимся, ес-ли — нет, то — расходящимся.
Теорема 56 (свойства сходящихся рядов).
(a) Пусть ^ un = S, тогда
n=1
у ^ αun = αS.
n= 1
(b) Пусть J2un = SHj2vn = T. Тогда.
n=1 n=1
J2(un + vn) = S + T.
n =1
11.2 Геометрический ряд
Геомет,рическим рядом или суммой {бесконечной) геометрической прогрессии называют ряд вида
^qn = 1 + q + q^ + q + ■ ■ ■ + qn 1 +
n =0
Пример 33. Примеры геометрических рядов:
| n- 1 n- 1 1) p + |
| + .... |
1 - p + p 2 - p 3 + ··· + (- 1 + 1 + 1 + ··· + 1 + ..., 1 - 1 + 1 - ··· + (- 1) n +1
Теорема 57. Для того чтобы геометрический ряд сходился, необходимо и достаточно, чтобы выполнялось неравенство
q <1
в этом случае
q
n=0
Доказательство. Выведем сначала вспомогательную формулу:
sn = 1 + q + q2 + q3 + ■■■+ qn-1 =
= 1 1-((1 -q)-(1 + q + q 2 + q 3 + --- + qn- 1)) =
q
= ------------ (1-q + q-q2 + q2 -q3 + ■■■+ qn-1 - qn) =
1-q
= 1 - qn
1-q.
Рассмотрим теперь конкретные случаи.
Если \q\ > 1, то lim qn = oo. Поэтому предел sn = 1 - -q не существует.
Если \q\ < 1, то lim qn = 0. Поэтому
1 -qn 1
lim s = lim
n ^оо n ^оо 1 - q 1 - q
в частности, этот предел существует.
Случаи q = =Ы будут рассмотрены в следующем параграфе. П
11.3 Необходимый признак сходимости
Теорема 58 (необходимый признак). Рассмотрим ряд ^ un- Если un
n= 1
не стремится к нулю (т. е. стремится к другому числу или вовсе не имеет предела), то ряд расходится.
Доказательство. Пусть ряд сходится. Заметим, что
sn - sn-1 = (u 1 + u 2 +------------------)
- (u 1 + u 2 +----------- un-1) = un.
Перейдем к пределу в равенстве sn - sn- 1 = un- Здесь sn стремится к S, и sn-1 тоже стремится к S. Поэтому если ряд сходится, то un стремится к S-S = 0.
Пусть теперь un не стремится к нулю, а ряд сходится. Тогда но пер
вому утверждению un должен стремится к нулю. Получается противо
речие! П
Закончим теперь доказательство теоремы 57. Пусть q = 1. Тогда ряд будет таким: 1 + 1 + 1 + 1 + .... Здесь un = 1 стремится к единице. Ряд расходится, так как un = 1 не стремится к нулю.
Пусть q = -1. Тогда un = (- 1) n - Эта последовательность не имеет предела. Ряд расходится, так как un не стремится к нулю.
11.4 Интегральный признак сходимости
Теорема 59 (интегральный признак). Пусть выполнены условия
(a) f(x) > 0;
(b) функция f убывает.
ОО +00
Тогда ряд ^ f(n) и несобственный интеграл J f(x)dx сходятся или
n=1 1
расходятся одновременно.
11.5 Гармонический ряд
(Обобщенным) гармоническим, называют ряд
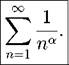
|
При α = 1 он превращается в обычный гармонический ряд ^ 1. Отсюда
n =1
— название.
Теорема 60. При \ α > 1 \ обобщенный гармонический ряд сходится, а
при α < 1 — расходится.
Задача 67. Какие из следующих рядов сходятся:
ОО 1 ОО 1 ОО 1
V2 V- V—
n n n
n=1 n= 1 n=1
11.6 Признак сравнения
Теорема 61. Даны два ряда
n =1 n =1
состоящие из неотрицательных слагаемых. Пусть
C = lim un.
Тогда если C = 0, оо, то оба ряда сходятся или расходятся одновременно. Пример 34. Исследовать на сходимость ряд
n =1 n =1
Решение. Сравним ряд со вспомогательным рядом ^ vn = ^ n 1 2 '.
n=1 n=1
C = lim u = lim ^ =
n ^ОО vn n^ОО 1
n2 г оо ^ n 2
= lim , = < — = lim
| n ^оо |
V n 4 + 1 OO n n 4(1 + n 1 4
n 2 1
lim =lim
| n 4 |
n 2 1+ 1 4 n→∞ 1+ n 1 4
1.
11.7 Признак Даламбера
Теорема 62 (признак Даламбера). Пусть дан ряд ^ un, в котором un >
n= 1
0, пусть сугцествует предел
q = lim.
n ^оо un
Тогда
(а) Если \q < 1
, то ряд сходится.
(Ь) Если q > 1, то ряд расходится, причем общий член un стремится к бескоиечиости.
Пример 35. Рассмотрим ряд Yl'^=1 2 n • Здесь un = 2 n, un+1 = 2 n + + 1 1. Имеем
un+1 (n + 1)-2 n (n + 1)-2 n
q = lim ------ = lim------------------ = lim
n^оо un n^оо 2 n +1 • n n^оо n • 2 n +1
1 n + 1 1 1
= - lim = -•1 = -.
2 n ^оо n 2 2
Правило: При вычислении предела
lim
n ^oo un
удобно располагать однотипные слагаемые друг над другом.
11.8 Знакочередующиеся ряды и признак Лейбница
В признаке сравпепия и в признаке Даламбера ряды состоят из неотрицательных слагаемых. Теперь будем рассматривать ряды, состоящие из слагаемых разных знаков. Наиболее часто знаки слагаемых чередуются. При этом ряды выглядят так:
| ^ (- 1) nwn, 5Z(- 1) n +1 |
∞∞
wn
n =1 n =1
где wn > 0. Такие ряды называют знакочередующимися.
Теорема 63 (признак Лейбница). Пусть дай знакочередующийся ряд и выполнены условия
(a) lim wn = 0;
n ^oo
(b) w1 > w2 > w 3 >....
Тогда ряд сходится.
Если условие (а) не вынолнено, то ряд расходится.
^ (- 1)" Задача 68. Исследовать на сходимость ряд 22 —
n n =1
Решение. Это знакочередующийся ряд, причем wn = 1 ■ Очевидно, условия
(а) lim wn = 0;
(Ь) w1 > w2 > w 3 >...
признака Лейбница выполнены. Поэтому ряд сходится. П
Замечание 5. В качестве приближенных значений к сумме S ряда обычно берут частичную сумму sn с большим n, т. е. S ~ sn- Оценка точности такого приближения в случае ряда, удовлетворяющего условиям признака Лейбница, решается просто. А именно,
Она позволяет оцепить, сколько слагаемых ряда надо взять, чтобы посчитать его сумму с заданной точностью.
Отсюда правило: Если хотят иметь точность 0,001, то выписывают члены ряда до тех пор, пока не появится слагаемое wn+1 меньшее 0,001. После этого все вьшисанпые слагаемые складывают — это и есть sn, обеспечивающее нужную точность.
11.9 Как выбрать признак для проверки числового ряда па сходимость
0. Универсальным способом проверки числового ряда на сходимость является только следующее: надо последовательно попробовать применить все 5 признаков (необходимый, Даламбера, Лейбница, сравнения и интегральный). По обычно выбор признака удается осуществить, пользуясь последующими правилами.
1. Если ряд является геометрическим или гармоническим, надо применить соответствующие теоремы {\q\ < 1 и α > 1).
2. Если ряд знакочередующийся, т. е. содержит (—1) n, то следует начать с признака Лейбница. Если условие (а) признака Лейбница не выполнено, то ряд расходится.
3. Если слагаемые ряда содержат геометрическую прогрессию и/или факториал, следует начать с признака Даламбера.
4. Если слагаемые ряда образованы только с помощью операций сложения, умножения и деления, т. е. являются отношением многочленов,
а также операции извлечения корня, то следует начать с признака сравнения, взяв в качестве второго (эталонного) ряда обобщенный гармонический ряд с подходящим (1.
5. Интегральный признак применяется неносредственно только к ря-
∞
дам тина V" l 1 n.
n=2
6. Если предыдущие правила пе подходят, следует применить необхо
димый признак.
11.10 Абсолютно и условно сходящиеся ряды
∞ ∞
Теорема 64. Если ряд ^|un| сходится, то ^ un тоуке сходится.
n=1 n=1
∞
Ряд ^ un называют абсолютно сходящим,ся, если сходится оп сам и
n =1
∞
сходится ряд Y^ |
n =1
Ряд Yn=1 "^п называют условно сходящимся., если сам ряд сходится,
| Е |
ОО I ∞n =1 |un| ^ расходится.
∞ ^ (- 1)" Задача 69. Исследовать па абсолютную и условную сходимость ряд 2_]—
n=1
Решение. Рассмотрим исходный ряд и ряд из модулей:
^(- 1) n ^1
/_^ п ' ^--1 п
n= 1 n =\
Второй ряд является гармоническим с а = 1; он расходится. Про пер
вый ряд из задачи 68 известно, что он сходится. Вывод: исходный ряд
сходится условно. П
| 2 n n =1 |
| Решение. Рассмотрим исходный ряд и ряд из модулей: ^(- 1) n ^1 |
| 2 n 2 n n =1 n =1 |
| Второй ряд является геометрическим с q = 1 2. Поскольку q < 1, on сходится. По теореме 64 первый ряд тоже сходится. Выво || сходный ряд сходится абсолютно. П |
(- 1)" Задача 70. Исследовать на абсолютную и условную сходимость ряд ∞ —
Глава 12
Степенные ряды
12.1 Факториалы
Факториалом, натурального числа п называют произведение всех натуральных чисел от 1 до п:
п! = 1 • 2 • ... • п.
По определению полагают
1! = 1, 0! = 1.
Пример 36.
(п + 1)! 1 •2- ... -п-(п + 1)
= п + 1.
п! 1 • 2 • ... • п
12.2 Определение степенного ряда
Степенным, рядом называют ряд вида
оо У^ СnХn = С0 + C 1 X + С2Ж2 + ..., n =0
где числа с n, называемые коэффициентами, являются заданными. Подчеркнем, что суммирование, как правило, начинается с нуля.
Пример 37. Например, степепной ряд ^ x n ! сходится к функции у = ex.
12.3 Теорема Абеля
Если в степенной ряд вместо х подставить конкретное число, то получится числовой ряд. Он может сходиться или расходиться. Множество
тех x, для которых степенной ряд сходится, называют множест.вом или областью сходимости степенного ряда.
Теорема 65 (теорема Абеля).
(а) Если степенной ряд в точке x^ сходится, то он сходится во всех точках \x\ < \x^\.
-I ^*1 О \х^\
(Ь) Если стеиенной ряд в x* расходится, то он расходится во всех точках
\x\ > \x*\.
-\х*\ о |;^*|
12.4 Интервал и радиус сходимости
Теорема 66. Для каясдого стененного ряда существует такое R G [0, +оо]. что при \x\ < R стеиенной ряд сходится, причем абсолютно, а при \x\ > R стеиенной ряд расходится, причем общий член стененного ряда не стремится к нулю. Таким образом, область сходимости стененного ряда представляет собой одно из четырех миоукеств: 1. (-R;R), 2. [-R;R), 3. (-R;R], 4. [-R;R].
Число R называют радиусом сходи,мост,и, а интервал (-R;R) — интервалом. сходимост^и степепного ряда. Интервал сходимости отличается от области сходимости пе более, чем на две крайние точки.
Сформулируем явно определение радиуса сходимости. Радиус сходимости — такое число R, что при \x\ < R степенной ряд сходится, а при \x\> R степеппой ряд расходится.
12.5 Нахож:дение радиуса сходимости
с помощью признака Даламбера
Теорема 67 представляет собой вариант признака Даламбера.
∞
Теорема 67. Радиус сходимости степенного ряда, ^ с^ж"^ можно найти
п=0
НО формуле
c
R = lim
| cn +1 |
n→∞
при условии, что этот предел существует.
Задача 71. Найти область сходимости степенного ряда
п+1
п=1
x
Решение. Найдем радиус сходимости. Воспользуемся для этого теоремой 67.
| ∞ ( 1)П+1 п=1 |
| n +1 |
| n 3 n 1 |
xn,cn
| (n + 1)3 n +1 1 (n + 1)3 n +1 |
"" = п3", ""+
c
| lim n 3 n n→∞ |
R = lim
| cn +1 |
n→∞
(n + 1)3 n +1 n + 1
| n 3 n |
| n n→∞ |
lim =3lim =3.
Итак, R = 3. Значит, (- 3,3) — интервал сходимости. Концами интервала сходимости являются точки ± 3. Проверим сходимость ряда на концах.
Подставим в степенной ряд первую концевую точку ж = 3:
| А^ - 3" п=1 |
| n 3 n x→ 3 n =1 |
у- (- 1) " +13,. = у- (- 1) ' +1
п=1 п=1
Это знакочередующийся ряд, для пего выполнены (задача 68) условия признака Лейбница. Поэтому он сходится.
Подставим в степенной ряд вторую концевую точку ж = - 3:
| n +1 |
А^ - 3"
п=1
v(- 1
x 3 n 3 n
n =1
3)
^ (- 1)-+1 2^ п3"
п=1
1) n 3 n
∞ 1 п=1
с точностью до знака это гармонический ряд с а = 1. По теореме 60 он расходится.
Ответ: Область сходимости (—3,3]. П
12.6 Ряд Маклбрена
Пусть дана функция у = f(x). Если удалось подобрать степенной ряд так, чтобы
п=0
ТО говорят, что функцию f разложили в степенной ряд.
Теорема 68. Если существует степенной ряд, сходящийся к функции f, то его коэффициенты Сп обязательно совпадают с числами
Сп = f ( )(0)- (12-1)
п!
Числа (12.1) называют коэффициентами Маклорена функции f, а степенной ряд
cnx
у- f (!)(0) xп
п=0
— рядом Маклорена функции f.
Замечание 6. Ряд Маклорена называют также рядом Тейлора в окрестности точки x 0 = 0.
К сожалению, ряд Маклорена функции f может не сходиться к функции f или сходиться не к функции f. Поэтому после выписывания ряда Маклорена функции f надо проверять, действительно ли он сходится к функции f. Это можно делать, например, с помощью следуюгцей теоремы.
Теорема 69 (условие разложимости). Если на отрезке [—г, г] функция f и все ее производные ограничены {по абсолютной величине) одной и той же копстаптой, то ряд Маклорена функции f сходится к f во всех точках отрезка [—г, г].
12.7 Ряд Маклорена функции y = ex
Теорема 70. Ряд Махлорена^ функции y = ex имеет вид
x 2 x 3 xn
| 2! 3! |
| n |
1+ x + + + ··· + +
Е
n= 0
xn
n!
и СХОДИТСЯ к ней на (—оо, +оо). Доказательство. Вытекает из теоремы 69.
12.8 Ряд Маклорена функции y = sin x
Теорема 71. Ряд Маклорена функции y = sin x имеет вид
| Е n= 0 |
x 3 x 5 sin x = x - 3! + 5!
+
| x |
2 n +1
(2 n + 1)!
+
2 n +1 ∞ x
(2 n + 1)!
и СХОДИТСЯ к ней на (—оо, +оо). Доказательство. Вытекает из теоремы 69.
12.9 Ряд Маклорена функции y = cos x
Теорема 72. Ряд Маклорена функции y = cos x имеет вид
| Е n= 0 |
2 n
| x |
x 2 x 4 cos x = 1 - 2! + 4! + ··· + (2 n)
+
2 n ∞ x
(2 n)
и СХОДИТСЯ к ней на (—оо, +оо). Доказательство. Вытекает из теоремы 69.
12.10 Ряд Маклорена функции y = l n (1 + x
Теорема 73. Ряд Маклорена функции y = ln(1 + x) имеет вид
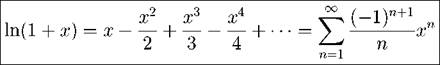
и сходится к ней на (—1,1
12.11 Ряд Маклорена функции y = (1 + x
α
Теорема 74. Ряд Маклореяа функции y = (1 + x) α имеет вид
| 2! |
| 3! |
1 + x) α = 1 + αx + α (α - 1) x 2 + α (α - 1)(α - 2) x 3 +
| Е α (α - 1)(α - 2) ... (α - n +1) xn n=0 |
И СХОДИТСЯ к ней на (- 1,1).
Этот ряд называют биномиальным.
12.12 Применение степенных рядов в приближ:енных вычислениях
Задача 72. Посчитать \ 29 с точностью до 0,001. Решение. Представим \ 29 в виде
29 = лУ27 + 2 = ^27(1 + 2) = 3у 1 +
2 27
и воспользуемся биномиальным рядом
| α (α - 1) 2 α (α - 1)(α - 2)3 1 + αx + ^ x + -------------------------------- x +... |
2! 3!
После подстановки α ^ и умножения на 3 получаем
3(1 + x)1 / 3 = 3 +
x
x 5 3
81 243
x
Для этого подставим в ряд x = 2 2 7:
з 2 2 4 40
371 + —= 3 +----------------- +-------------- ...
27 27 2187 531441
= 3 + 0,07408 - 0,00183 + 0,0000753 -....
В соответствии с правилом, описанным в замечании 5, выписанные сла
гаемые обеспечивают точность не менее 0,0000753. Просуммировав их,
получаем ответ: ^^29 f«3 + 0, 07408 - 0,00183 = 3,07232. П
Задача 73. Вычислить
f 1 /2 dt
л/ 1 + t
с точностью до 0,001.
Решение. Разложим сначала в степенной ряд функцию y =
1+ t
л/1+ t 2! 3!
= 1+ 2t+ 2! + 3!
1 3 2 5 3 35 4 63 231
= 1 --t + -t------ r +---- t-------- t 5 +---- 6 -
2 8 16 128 256 1024
Проинтегрируем этот ряд:
| dt 121354 75 -- x ------ x__ + _ x -- - x_ + ------ x |
| л/ |
| 216 337 x + x |
| 512 1024 tndt |
x t n+1 x x n+1 0 n+1 x n+1
0 n + 10 n + 1 n + 1 n + 1
Подставим в него x = 2'-
0 -^^ = 0,5 - 0,0625 + 0, 015625 - 0,004883+
+ 0, 001710 - 0, 0006409 + ....
В соответствии с правилом из замечания 5 эти слагаемые обеспечивают точность не менее 0,0006409. Просуммировав их, получаем ответ: 01 / 2 1 dt^ 0,5-0, 0625 + 0,015625 - 0,004883 + 0,001709 = 0,449951.
1+ t
 2014-02-24
2014-02-24 451
451