Под действием вертикальной рефракции визирный луч искривляется и вместо отсчета по рейке в точке а (b), когда отсутствует рефракция, получают отсчет в другой точке a’(b’). Превышение h, свободное от влияния нивелирной рефракции равно
h = a – b = (a’ – b’) + (aa’ – bb’) = h’ + δh,
где h’ = (a’ – b’) – измеренное превышение, δh = aa’ – bb’ – поправка за рефракцию. В солнечную жаркую погоду летом при низком прохождении визирного луча над почвой и сравнительно больших расстояниях от нивелира до реек нивелирная рефракция может существенно искажать результаты нивелирования, особенно на наклонных трассах большой протяженности.
Теоретически строгая формула для вычисления поправок за рефракцию в отсчеты по рейкам при нивелировании имеет вид
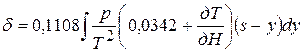 .
.
Значение р / Т2 = 0,009 практически постоянно на всем пути визирного луча в каждый фиксированный момент времени. Поэтому давление и температуру достаточно измерить на высоте визирного луча вблизи трубы нивелира в период наблюдений на станции. Гораздо сложнее определить градиенты температуры воздуха на всем пути визирного луча в момент производства отсчетов по рейке. Не зная реальных значений градиентов на пути визирного луча в момент отсчета по рейке, нельзя вычислить поправку за рефракцию. В нижнем трехметровом слое воздуха градиенты температуры непрерывно изменяются в пространстве и во времени даже при незначительном изменении высоты элементарного слоя воздуха над почвой. Наибольшей величины градиенты достигают в полуденное время, а также после полуночи, причем днем они существенно больше по модулю, чем ночью. В суточном ходе градиенты температуры утром и вечером переходят через нуль, изменяя при этом всякий раз знаки на противоположные.
Для получения количественных оценок влияний рефракции на отсчеты по рейкам и на превышения на станциях преобразуем формулу (1) к более простому виду, полагая при этом, что в момент отсчетов по рейкам известны средние значения Е вертикальных градиентов температуры воздуха (град/м) на пути визирного луча между нивелиром и рейкой:
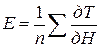 ,
,
а также средние значения температуры и давления. Формула (1) после интегрирования, с учетом средних на пути луча значений Е, р и Т, примет вид
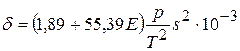 .
.
Обозначим среднее значение градиентов температуры на пути визирного луча до задней рейки ЕЗ, а до передней рейки ЕП. Тогда поправка в превышение на станции будет равна
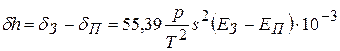 .
.
 2014-02-24
2014-02-24 1353
1353
