Задача численного дифференцирования состоит в приближенном вычислении производных функции u(x) по заданным в конечном числе точек значениям этой функции. Пусть на [a,b] введена сетка:
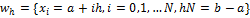 ,
,
И определены значения ui=u(xi) функции u(x) в точках сетки. В качестве приближенного значения u’(xi) можно взять, например, любое из следующих разностных отношений:
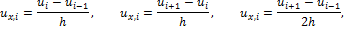
В качестве примера рассмотрим функцию
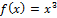 ,
,
для которой производная равна 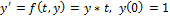 .
.
Это уравнение имеет точное решение 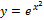 .
.
Код для реализации метода Эйлера показан в листинге
Листинг 15.5. Решение уравнения методом Эйлера
a = 0; b = 2; m = 50;
dx = (b - a) / m;
x = 0, y = 1;
for (int i = 1; i <= m; i++)
{
y += dx*F(x,y);
x += dx;
g.DrawEllipse(Pens.Black, II(x) - 2,
JJ(y) - 2, 4, 4);
}
Для симметричной схемы уравнение (6) принимает вид:
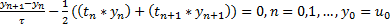
и его удается решить явно:
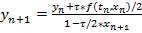 .
.
Код для решения уравнения по симметричной схеме представлен ниже:
Листинг 15.6. Решение уравнения по симметричной схеме
a = 0; b = 2; m = 50; dx=(b-a)/m; x = 0; y = 1;
for (int i = 1; i <= m; i++)
{
y = (y+dx/2*F(x,y))/(1-(x+dx)*dx/2);
x += dx;
g.FillEllipse(myBrush,II(x)-3, JJ(y)-3,6,6);
}
В следующем листинге 15.7 представлен код для реализации метода Рунге-Кутта:
Листинг 15.7. Решение уравнения методом Рунге-Кутта
a = 0; b = 2; m = 50;
dx = (b - a) / m;
x = 0; y = 1; yt = 0;
for (int i = 1; i <= m; i++)
{
yt = y + dx / 2 * F6(x, y);
y = y + dx / 2 * F6(x + dx / 2, yt);
x += dx;
g.FillEllipse(myBrush,II(x)-2,JJ(y) - 2, 4, 4);
}
На рис. 15.6 на интервале [0,2] представлено точное решение (сплошная линия), приближенное решение по методу Эйлера (маленькие черные точки), по симметричной схеме (большие черные точки) и методом Рунге-Кутта (белые точки).
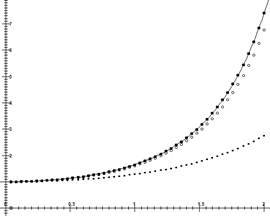
Рис. 15.6. Сравнение точного и приближенных решений линейного уравнения
Из рис. 15.6 видно, что метод приближенного решения по симметричной схеме дает более точное решение.
 2014-02-24
2014-02-24 674
674







