Обратное резерфордовское рассеяние

По-русски иногда сокращают ОРР и приводят с расшифровкой. В английском языке устоялось сокращение RBS (Rutherford Backscattering). Название метод получил в честь знаменитого опыта Резерфорда с α-частицами.

В данном методе образец бомбардируют легкими высокоэнергетическими ионами Н⁺, Не⁺, которые теряют свою энергию преимущественно за счёт электронного торможения. Вклад в энергетические потери со стороны ядерного торможения связан в первую очередь с эффектами рассеяния налетающих ионов. Изучение энергетического спектра обратно рассеянных легких высокоэнергетических ионов и составляет основу метода обратного резерфордовского рассеяния.

Поскольку энергия рассеянного иона зависит как от природы атома в образце, на котором произошло рассеяние, так и от того, на какой глубине произошло рассеяние, т.е. от пути, пройденного в твердом теле сначала налетающим, а затем – рассеянным ионом, то открывается возможность в неявном виде установить, как абсолютный элементный состав образца, так и получить информацию об изменении состава образца по глубине.

Под номером 1 – ускоритель ионов, роль которого выполняет либо электростатический генератор, либо в случае высокой энергии циклотрон. Энергия ионов велика и лежит в диапазоне 0,5 – 6 МэВ. Для большинства опытов достаточно 2 – 2,5 МэВ. Пучок ионов 2 попадает на поверхность образца 3, рассеивается под углом θ и регистрируется барьерным детектором 4. К диодной структуре барьерного детектора (золото – кремний) приложено внешнее напряжение, что приводит к искривлению зон в кремнии и создает условия для разделения электронно-дырочных пар, образующихся в кремнии при поглощении ионов.

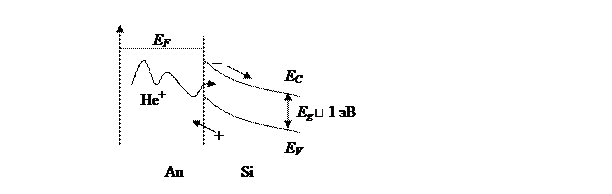
Число образующихся электронно-дырочных пар равно отношению энергии налетающего иона к ширине запрещенной зоны (около 1 эВ). В результате, при поглощении ионов во внешней цепи регистрируются импульсы тока импульсы тока, интенсивность которых пропорциональна энергии поглощенных ионов. Подсчёт этих импульсов при помощи многоканального анализатора даёт распределение ионов по энергии.

Геометрия эксперимента выбирается таким образом, чтобы потери энергии при рассеянии максимальны (чтобы было что мерить), поэтому стремятся, чтобы угол θ был близок к 180°. Вследствие конечных размеров детектора это невозможно и, как правило, θ = 160-170°. Для интерпретации данных обратного резерфордовского рассеяния принципиально то, что эффекты рассеянии описываются простейшими кинематическими уравнениями, причем в силу малости эффектов ядерного торможения рассеяние можно считать однократным и потеря энергии налетающим и рассеянным ионом может быть представлена в виде двух аддитивных вкладов, соответствующих рассеянию на ядрах и торможению на электронных оболочках, т.е. за счёт электронного возбуждения.

Итак, мы бомбардируем поверхность образца ионами с энергией Е_{0 .} Потери энергии при рассеянии будут включать потерю энергии на пути к точке рассеяния 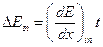, где t – глубина вхождения, а также потери, связанные с рассеянием , К – кинематический фактор, а именно отношение энергий иона до и после рассеяния, которое зависит только от массы взаимодействующих частиц и от угла рассеяния. Величины кинематического фактора табулированы и являются индивидуальной характеристикой химического элемента. Вторая составляющая (энергия налетающего иона на глубине t) находится следующим образом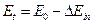. Потери энергии при выходе .

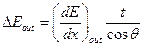Энергия покидающего образец иона равна:

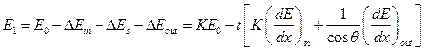
Пользоваться этим уравнением сложно, поскольку значения тормозных факторов в целом меняются по мере торможения иона, однако можно показать, что для абсолютного большинства химических задач хорошим является так называемое поверхностное приближение. Это значит, что фактор торможения на траектории входа приравнивается к фактору торможения в точке непосредственного входа. На выходе же – как начальная энергия, умноженная на кинематический фактор. Иначе говоря, считается, что рассеяние происходит лишь в точке входа.

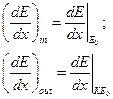
Тогда

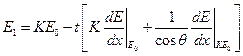
Для удобства расчётов была введена величина сечения торможения, табулированная в расчёте на один атом.

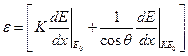
Но поскольку это величина на один атом, конечное значение энергии выразится:

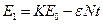
Значения ε также табулированы для различных энергий. (N – величина концентрации атомов элемента)

Это уравнение устанавливает связь как с элементным составом образца (через кинематический фактор), так и с количественным составом. Это уравнение также отражает основные особенности процесса рассеяния легких ионов, а именно: торможение и рассеяние на электронных оболочках и на ядрах протекают как независимые процессы.

Спектры ОРР имеют сложную форму, и при их анализе принимают во внимание ряд характерных параметров, а именно:

· положение краев в спектре, связанных с рассеянием на атомах различных элементов

· выходы рассеяния

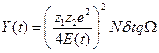
Y(t) – выход на глубине рассеяния, z_i – атомные номера для налетающих ионов и атомов образца, E(t) – энергия налетающего иона в момент столкновения, N – концентрация атомов элемента, на которых происходит рассеяние, δt – тонкий слой, выделенный на глубине, q – число налетающих ионов, т.е. заряд, Ω – телесный угол детектора.

1) 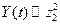, чем выше порядковый номер элемента в образце, тем интенсивнее он рассеивает налетающие ионы;

2) , выход рассеяния растет по мере проникновения ионов вглубь образца.

Пример. Однородный одноэлементный массивный образец.

Ионы налетают на образец, рассеиваются и имеют энергию 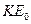– максимально возможная энергия – край спектра. Ионы, рассеянные с глубины t₁ будут иметь энергию 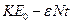, но интенсивность будет выше (см. 2).

Пример. Двухкомпонентный массивный образец, причем оба элемента распределены однородно. Спектр является суммой спектров, соответствующих рассеянию на атомах разных элементов.

Обозначим

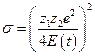
Тогда величина поверхностного рассеяния для элементов А и В может быть найдена следующим образом:

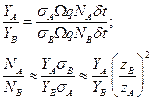
Это позволяет найти состав образца в виде соотношения концентраций атомов входящих в его состав элементов. Понятно, что были введены некоторые допущения, однако это позволяет добиться точности выше 0,95.

До сих пор мы рассматривали образцы, не имеющие внутренней структуры, хотя и отмечали, что поскольку налетающие частицы проникают в образец, можно изучать изменение состава по глубине.

Пример. Двухслойная система, в которой на подложку из более легкого элемента В нанесена пленка элемента А.

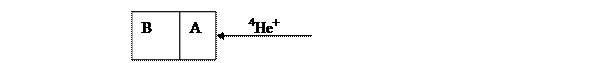
Элемент А проявится в виде интенсивного пика (зарядовое число выше, чем для В). Положение края этого спектра соответствует 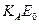. Ионы гелия, прошедшие через пленку, начинают рассеиваться на В, однако в силу больших потерь энергии при прохождении через плёнку А край спектра будет лежать в области более низких энергий.

В данном спектре

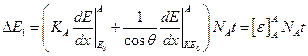
Т.е. измеряя данную величину из спектра, можно определить толщину нанесенной пленки, точнее, количество элемента А, нанесенного на поверхность элемента В, т.е. величину 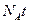. Геометрическую же толщину мы можем найти только на основании допущений о плотности пленки А.

На выходе из пленки А энергия зондирующих электронов составит

Именно такую энергию будут иметь ионы, когда начнут рассеиваться на атомах В. Тогда энергия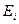, связанная с положением края спектра В, выразится так:

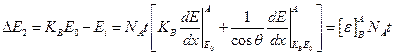
Подобная краткая запись показывает, что рассеяние происходит на атомах В, а торможение – на атомах А.

Пример. Подложка из TiO₂, на поверхность нанесена Pt. Спектр ОРР имеет вид:

Метод ОРР особенно эффективен для определения малых количеств тяжелого элемента. При этом надо иметь в виду, что с ростом зарядового числа атомов образца постепенно теряется возможность к точному определению природы тяжелого элемента. Дело в том, что значения кинематического фактора при больших z отличаются уже незначительно, и отличить, например, пик от платины и пик от палладия в спектрах РР оказывается затруднительно. Т.е. элементная чувствительность растет, а возможность качественного определения элементного состава снижается.

Количественный анализ в методе ОРР базируется на использовании формулы Резерфорда:

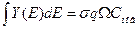
Площадь пика даёт поверхностную концентрацию элемента. Метод позволяет определять количества элементов в долях монослоя (до 0,1 монослоя). Монослой – условная величина для конкретного элемента, обозначающая плотнейшее заполнение.

Если нанесена ещё и медь, то она проявится в виде отдельного пика с интенсивностью, пропорциональной зарядовому числу в квадрате.

Если поверхностную концентрацию увеличивать, то график будет меняться:

Пример. Предположим, что у нас имеется алюминиевая фольга, на поверхность которой напылено золото.

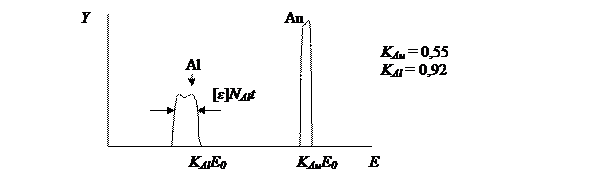
Различие кинематических факторов довольно велико.

Если золото напылить на обе поверхности, можно рассчитать толщину фольги на основании данных спектра.

Пример. Рассмотрим поверхностное окисление кремния. Пусть имеется кремниевая пластинка, которую мы окислили с поверхности так, что образовалась пленка SiO_2­.

Концентрация кремния в оксиде меньше, чем в кремнии, образуется выбоина, которая соответствует SiO₂. Она увеличивается при увеличении толщины плёнки оксида.

Может показаться, что в спектре присутствует три пика, а значит, три компонента. Это неправда, просто один из компонентов имеет неравномерное распределение.

Следующий пример показывает, что ОРР позволяет зондировать образец на глубину 1000 нм и получать информацию о трансформации образца в пределах этого слоя.

Пример. Ограничимся высокоэнергетической частью спектра оксида висмута на висмуте, не рассматривая вклад кислорода. Было установлено, что пленка оксида висмута может восстанавливаться при приложении соответствующего потенциала. Можно предположить три механизма восстановления. На практике реализуется механизм 3.

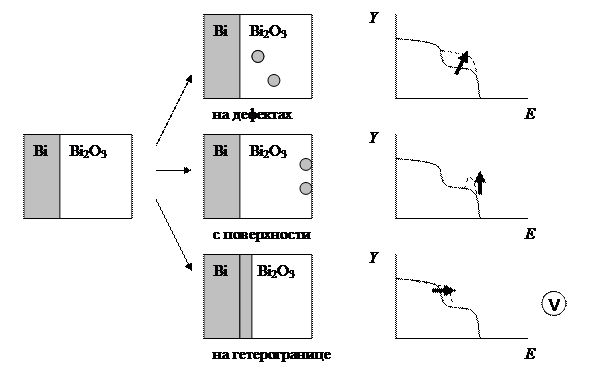
Пример. Исследование многослойных систем. На подложку из кремния напыляют никель, затем нагревают и на гетерогранице происходит образование силицида никеля.

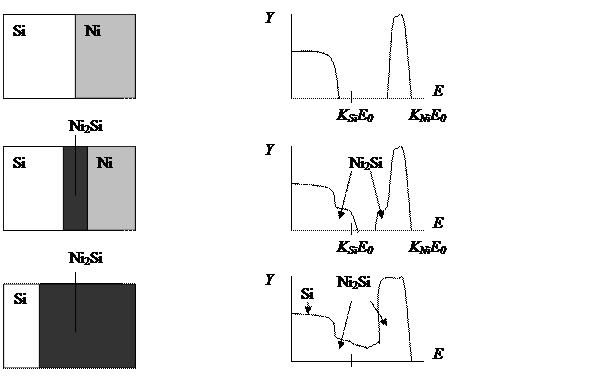
Поскольку на поверхности сохраняется тонкая плёнка никеля, то край спектра кремния не достигнет значения 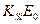. Общая площадь пика, соответствующая никелю, останется при этом неизменной. Если греть дальше, то в результате вжигания никеля в подложку, образуется слой силицида никеля на слое кремния. Пик рассеяния для никеля теряет структуру, т.к. в пределах слоя силицида никель распределен равномерно. Край рассеяния для кремния достигает значения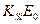, поскольку кремний в составе силицида выходит на поверхность. Таким образом, с помощью ОРР можно исследовать кинетику процесса, каковым является синтез силицида в результате прогрева кремния и никеля.

Одним из крупнейших достоинств метода является то, что он не разрушает образец. В частности, он широко использовался для исследования археологических образцов.

Среди задач ОРР имеется возможность определения профилей распределения примесей по глубине образца. Эти измерения можно выполнять в том случае, когда примесь тяжелого элемента распределена в относительно более легкой матрице.

Предположим, что в результате облучения внутри полимера возникли поры, в которые затем адсорбировали молекулярный йод, который распределился внутри пор. Анализируя форму спектров такого рода, можно установить пространственное распределение примеси по глубине.

Система А_хВ_1-х, в которой распределение меняется вглубь.

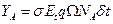(1)

Мы можем проводить определение концентрации в пределах некоторого тонкого слоя.

, (2)

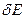– разрешение, с которым определяется энергия налетающих ионов.

Вводится рекуррентное (возвратное, периодическое) соотношение. Примем во внимание правило Брэгга: для многокомпонентных образцов вклад в тормозную способность аддитивно зависит от состава.

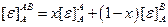
Итак,

Из уравнения (1) на основании данных об интенсивности рассеяния мы рассчитываем х. Потом по уравнению (2) рассчитываем 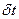– шаг движения вглубь. Затем мы сдвигаемся вглубь: 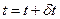, а затем рассчитываем величину ­– это энергия зондирующих частиц после передвижения вглубь на .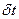

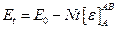
Затем процедура повторяется ещё и ещё раз, пока не исчерпаются данные об эффективности рассеяния компонента А.

Если речь идёт о выполнении аналитических измерений, нас будет интересовать предельная чувствительность, которая определяется очень слабыми, но всё же имеющими место эффектами распыления поверхности образца при бомбардировке ионами. Теоретически и экспериментально было показано, что абсолютный предел обнаружения по тяжелым элементам (в данном случае, золото) составлял 5·10¹¹ ат/см². В целом, реально достижимая предельная величина в случае золота составляет 5·10¹² ат/см², что составляет 1/1000 монослоя.

Если учитывать, что чувствительность метода зависит от зарядового числа определяемых элементов, то усреднено можно считать, что чувствительность метода составляет единицы – сотые монослоя.

Надо иметь в виду, что возможность по проведению качественного определения, как уже отмечалось, уменьшается при переходе к тяжелым элементам.

Важнейшим достоинством ОРР является возможность определения абсолютных концентраций. Значения концентрации, определенные путем интегрирования пиков, находятся без использования эталонов. Поэтому метод ОРР является важным источником калибровочной информации для других методов исследования.

ОРР позволяет также эффективно определять соотношение элементов как на поверхности образца, так и на внутренних границах раздела. При этом стехиометрический состав может быть определен с точностью до 5% с использованием простейшего соотношения

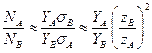
Имеются методы учета всех отброшенных при выводе этого метода факторов, которые позволяют определить х с точностью до сотых. Так можно выяснять степень стехиометричности полупроводниковых соединений и материалов.

При построении профилей глубинного распределения примесей из спектров ОРР разрешение по глубине составляет 10-20 нм.

Поскольку

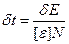и ,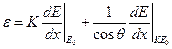

выполняя метод с помощью геометрии скользящих углов, можно увеличить разрешение до 2 нм, если этому не препятствует высокая шероховатость поверхности. При этом энергетические потери уменьшаются, уменьшается и глубина зондирования.

Достоинства метода ОРР:

· возможность определения очень малых концентраций, особенно в случае тяжелых элементов;

· возможность определения абсолютных концентраций;

· возможность исследования химических процессов в твердом теле и построения глубинных профилей распределения примесей;

· возможность определения толщин тонких пленок из спектров, однако, с точностью, определяемой допущениями по поводу плотности материала;

· метод является неразрушающим методом качественного и количественного анализа.

Ограничения метода:

· низкая чувствительность при определении легких элементов;

· потеря возможности проведения качественного анализа в случае тяжелых элементов;

· сложности и неоднозначности в интерпретации спектров (требуется привлечение дополнительной информации);

· невозможность получения профилей распределения лёгкой примеси в тяжелой матрице.