Перемещение частицы материала в потоке воздуха

Скорость витания твердой частицы в воздухе. Рассмотрим свободное падение твердой частицы в неподвижном воздухе. Частица, имеющая массу m, свободно, без толчка, падает из точки О, которую примем за начало координат. Ось х направим вертикально вниз (рис XIII.1.).

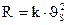
Р = тg

Рис. XIII.1. Падение материальной точки в неподвижном воздухе.

Под действием силы тяжести P = mg частица будет падать, все время оставаясь на оси х. В первый момент времени частица будет падать с ускорением g, но так как воздух оказывает сопротивление ее движению, через некоторое время частица станет падать без ускорения - с постоянной скоростью. Таким образом, скорость падения частицы в вязкой среде не может беспредельно возрастать, а с течением времени достигает некоторого наибольшего значения 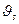, которое и сохраняется во все последующее время падения.

Очевидно, что если твердую частицу поместить в восходящий поток воздуха, то при определенной скорости этого потока частица "зависнет" в нем, т.е. будет витать.

Скорость восходящего потока воздуха, при которой твердая частица не будет иметь вертикального перемещения, равна постоянной скорости падения частицы в неподвижном воздухе. Такую скорость называют скоростью витания.

На твердую частицу действуют две силы: сила тяжести P=mg, направленная вниз, и сила сопротивления воздуха 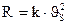(k — коэффициент пропорциональности), пропорциональная квадрату скорости и направленная вверх.

При достижении падающей частицей постоянной скорости Р = R и 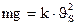, откуда

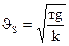, (31.1)

где g — ускорение свободного падения, м/с².

Сопротивление среды движущемуся в ней телу можно представить в виде зависимости

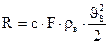, (31.2)

где с — коэффициент, являющейся функцией числа Re; F — площадь проекции тела на плоскость, перпендикулярную вектору скорости, м²; 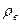— плотность среды (воздуха), кг/м³.

Следовательно, коэффициент пропорциональности k будет равен:

,

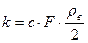а скорость 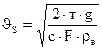. (31.3)

Коэффициент с может быть определен по формуле Л.С. Клячко, дающей хорошую сходимость с экспериментами до значений числа Rе = 2000:

.

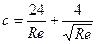Для значений числа Rе < 1 с достаточной для практики точностью можно принимать с = 24/ Rе.

Подставляя это значение с при развернутом виде числа 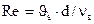в формулу (31.3) получим:

,

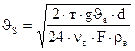или

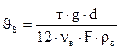. (31.4)

Для частицы имеющей форму шар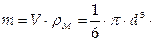а:

, а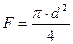

и следовательно, выражение (15.4) примет вид

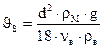или 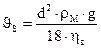, (31.5)

где d — диаметр частицы, м; 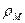— плотность материала, кг/м³; 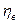— динамическая вязкость воздуха, Па ^ос.

Формула (31.5) справедлива лишь для частиц, имеющих форму шара, и при значениях числа Re <l. Для частиц иной формы вид зависимости для массвой скорости значительно усложняется; формула (15.5) может применяться только для пыли с шаровидной формой частиц размером не более 100 мкм.

Скорость витания частиц, отличающихся по форме от шара и имеющих большие размеры, определяется по эмпирическим формулам, справедливым лишь для определенной формы частиц данного материала.

Для определения скорости витания древесных материалов или отходов существует несколько эмпирических формул, одна из которых, предложенная Ленинградской лесотехнической академией имени С. М. Кирова, имеет вид

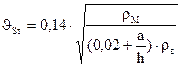, (31.6)

где а — коэффициент, зависящий от формы частиц: при квадратном поперечном сечении а =1,1, при прямоугольном поперечном сечении а =0,9; h — толщина частицы, мм; r_в- плотность воздуха, кг/м³.

Скорость трогания. Одиночная частица, лежащая на внутрен­ней поверхности горизонтального участка воздуховода, при некоторой скорости воздушного потока сдвигается со своего места и начинает перемещаться по длине воздуховода. Минимальную скорость движения воздуха, при которой частица начнет сдвигаться, называют скоростью трогания.

Л.С. Клячко для скорости трогания рекомендует следующую формулу:

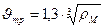, (31.7)

где 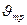— скорость трогания частицы, м/с; r_м-плотность материала, кг/м³.

В момент трогания на лобовой поверхности частицы, обращенной в сторону вектора скорости движения воздуха, создается некоторое давление, причем на нижней ее части оно будет больше, чем на верхней.

При скорости движения воздуха, большей скорости трогания, подъемная сила может превысить силу тяжести, и тогда частица оторвется от поверхности стенки воздуховода и окажется в потоке воздуха. Когда давление снизу и сверху частицы сделается одинаковым, частица начнет опускаться и вновь окажется на поверхности стенки воздуховода - коснется ее. Далее картина движения частицы повторится. Дальнейшее увеличение скорости потока при­ведет к увеличению расстояния от одного касания до другого.

Относительная скорость. Находясь в потоке воздуха, твердая частица перемещается со скоростью, меньшей, чем скорость движения воздуха. Отношение скорости движения частицы, находящейся в потоке воздуха, к скорости движения воздуха называют относительной скоростью:

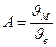, (31.8)

где 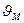— скорость движения твердой частицы материала, м/с, 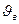— скорость движения воздуха, м/с.

В момент трогания частицы относительная скорость равна нулю. При скорости движения воздуха, большей скорости трогания, относительная скорость А всегда меньше единицы. Увеличение скорости движения воздуха приводит к увеличению относительной скорости и к более устойчивому

движению частицы в потоке воздуха.

При некоторой скорости движения воздуха в горизонтальном участке воздуховода, называемой критической скоростью, относительная скорость А приобретает максимальное значение.

Критическая скорость движения воздуха для горизонтального участка воздуховода зависит от формы и размера частиц, их плотности, от концентрации смеси и плотности воздуха.

Транспортирующая скорость. Скорость движения воздуха в воздуховоде, при которой происходит транспортирование материала, называют транспортирующей скоростью. Эта скорость должна быть несколько больше критической скорости.

Для нахождения транспортирующей скорости древесных материалов и отходов ЛТА имени С.М. Кирова предложена следующая эмпирическая формула:

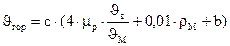, (31.9)

где 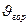— транспортирующая скорость движения воздуха в горизонтальном участке воздуховода, м/с; с — коэффициент, учитывающий снижение скорости перемещения материала в местных сопротивлениях системы (отводы, тройники и другие элементы системы); для внутрицеховых систем с частым расположением отводов с =1,1...1,15, для межцеховых систем длиной до 30 м с =1, 05... 1,1, длиной более 30 м с =1; 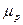— массовая расходная концентрация смеси, равная G_M / G_в; 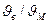— величина, обратная средней относительной скорости 1/ А; b — коэффициент, зависящий от вида транспортируемого материала.

Формула (31.9) применима только для измельченной древесины при .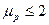

При транспортировании смеси воздуха и материала по вертикальным участкам системы воздуховодов с такой же скоростью, как и по горизонтальным, действие силы тяжести перемещаемых частиц приводит к увеличению концентрации смеси в вертикальных участках. Увеличение здесь концентрации смеси будет происходить непрерывно. При этом концентрация может значительно превысить расчетную, в результате чего вертикальные участки воздуховода забьются транспортируемым материалом. Чем больше высота вертикального участка, тем больше вероятность его забивания. Забиванию вертикальных участков способствует еще и то, что каждому из них предшествует отвод, в котором происходит снижение скорости движения

материала.

Для предотвращения закупорки вертикальных участков воздуховодов скорость движения смеси в них, должна быть больше скорости ее движения в горизонтальных участках на значение скорости витания

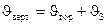. (31.10)

Увеличение скорости движения в вертикальных участках достигается путем уменьшения их сечения. Переход с большего сечения на меньшее следует устраивать в конце горизонтального участка, предшествующего вертикальному, с таким расчетом, чтобы после перехода до отвода оставался участок стабилизации длиной, равной пяти-шести диаметрам воздуховода.

Затраты энергии потока на подъем транспортируемого материала. При прохождении транспортируемого материала снизу вверх по вертикальным участкам воздуховодов на подъем материала затрачивается работа.

Напишем уравнение мощности:

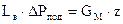, (31.11)

где L_в — объемный расход воздуха, м³/ч; 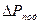— потери давления на подъем материала. Па; G_М — массовый расход материа­ла, кг/ч; z - высота подъема, м.

Отсюда потери давления на подъем материала

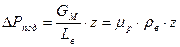, (31.12)

где 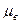— массовая расходная концентрация смеси;

Так как скорость подъема материала меньше скорости движения воздуха и равна 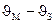то в формулу следует ввести поправку на различие скоростей движения материала и воздуха. С поправкой на скорости формула (31.12) примет вид

,

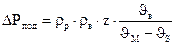где 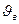— скорость движения воздуха в вертикальном восходящем потоке, м/с; 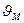— расчетная скорость движения материала, м/с; 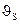— скорость витания, м/с.