2014-02-09
347Пусть стержень нагружен произвольной поперечной нагрузкой. Вырежем на некотором расстоянии z бесконечно малый элемент dz (рис.47). На данный элемент действует внешняя нагрузка и внутренние поперечные силы и изгибающие моменты в сечениях, по которым вырезан элемент.
 | |||
 |
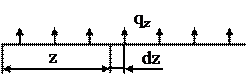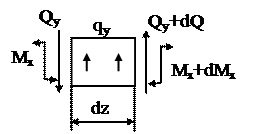Рис.47
Составим уравнения равновесия вырезанного элемента.
Уравнение равновесия всех сил на вертикальную ось.
- Qy + qy×dz + Qy + dQy = 0,
,
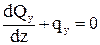Qy’ + qy = 0. (96)
Уравнение равновесия моментов относительно центра тяжести правого сечения вырезанного элемента.
- Мх + qy×dz×dz/2 + Мх + dМх - Qy×dz = 0,
слагаемое, выражающее момент от распределенной нагрузки, второго порядка малости, поэтому им можно пренебречь
,
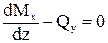Мх’ = Qy. (97)
Объединяя дифференциальные уравнения (96) и (97), получим:
Мх'' = - qy (98)
Решение данного дифференциального уравнения с правой частью состоит из двух частей общего и частного решения и имеет вид
Мх(z) = C1+С2z – Фм,
где Фм – частное решение, отражающее внешнюю приложенную нагрузку.
Определим физический смысл постоянных интегрирования. При z=0
Мх(0) = C1,
Мх’(0) = Qy(0) = С2.
Рассмотрим подробнее частное решение. Пусть стержень нагружен произвольной распределенной нагрузкой (рис.48). Определим величину поперечной силы и изгибающего момента для точки с координатой z.
 |
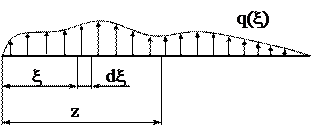Рис.48
Qy =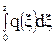 
,
Мх =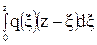 
. (99)
Значения интегралов зависят от внешней приложенной нагрузки. Рассмотрим значения нагрузочных функций для наиболее часто встречающихся нагрузок.
а) сосредоточенная сила (рис.49):
 |
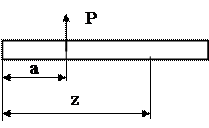Рис.49
при z£a ФQ(z)=0
ФМ(z)=0
при z³a ФQ(z)=-P
ФМ(z)=-P(z-a)
б) распределенная нагрузка (рис.50):
 |
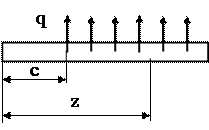Рис.50
при z£c ФQ(z)=0
ФМ(z)=0
при z³c ФQ(z)=-q(z-c)
ФМ(z)=-q(z-c)2/2
в) сосредоточенный момент (рис.51):
 |
Рис.51
при z£b ФQ(z)=0
ФМ(z)=0
при z³b ФQ(z)=0
ФМ(z)=-L
