2014-02-09
1212
Опыт и теория показывают, что в разных прозрачных средах свет распространяется с различными скоростями, меньшими скорости света в вакууме.
Среда, во всех точках которой скорость распространения света одинакова, называется оптически однородной. Рассмотрим, используя волновую теорию, явление отражения и преломления монохроматического света на плоской границе раздела двух различных, оптически однородных сред. Монохроматическому свету соответствует какая-либо одна длина волны или, говоря о субъективном восприятии, какой-либо один цвет.
|
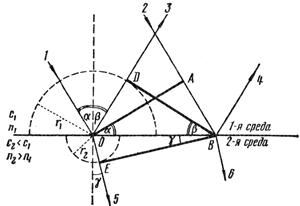Пусть плоский фронт световой волны ОА падает на границу раздела двух сред, скорости света в которых с 1 и с 2 < с 1 (рис. 3.1). Связанные с этим фронтом лучи 1 и 2 составляют с нормалью к границе раздела угол α. На границе раздела свет частично отражается (лучи 3 и 4), и частично проходят (преломляются) во вторую среду (лучи 5 и 6). Применяя принцип Гюйгенса, построим фронт отраженной и преломленной волны. В точку В 2 луч приходит позднее, чем 1 луч в точку О, на время t = | АВ |/ с 1. За это же время из точки О (как из вторичного источника света) в первой среде успевает распространиться полусферическая волна радиусом r 1 = c 1 t = | АВ |, а во второй среде – полусферическая волна радиусом r 2 = с 2 t = | АВ | c 2/ c 1.
|
Из рис. 3.1 видно, что ∆ ОАВ = ∆ ВDО (как прямоугольные, имеющие общую гипотенузу и по одному одинаковому катету: ОD = r = АВ). Поэтому угол АОВ = углу DВО. Но угол АОВ = α, а угол DВО = β (как углы со взаимно перпендикулярными сторонами), следовательно,
α = β, (3.1)
где β – угол отражения.
Падающий и отраженный лучи лежат в одной плоскости с перпендикуляром, проведенным к границе раздела сред в точке падения; угол падения равен углу отражения (закон отражения света).
Возвращаясь к рис.3. 1, учтем, что
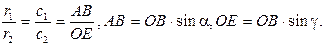
Тогда
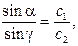(3.2)
где γ – угол преломления.
Падающий и преломленные лучи лежат в одной плоскости с перпендикуляром к границе раздела сред, проведенным в точку падения; отношение синуса угла падения к синусу угла преломления равно отношению скорости света в первой среде к скорости света во второй среде (закон преломления света).
Из формулы (3.2) следует, что при α = 0 будет и γ = 0 (так как с 1/ с 2 ≠ 0), т. е. луч, падающий нормально на границу раздела сред, не преломляется. Обозначим
с 1 = с / n 1 и c 2 = c / n 2,
где с – скорость света в вакууме, а n 1 и n 2 – безразмерные величины, называемые абсолютными показателями преломления первой и второй сред. Абсолютный показатель преломления показывает во сколько раз скорость света в данной среде меньше скорости света в вакууме. Очевидно, что абсолютный показатель преломления вакуума равен единице.
Учитывая, что показатели преломления двух сред обратно пропорциональны скоростям распространения света в этих средах, можно записать закон преломления в виде
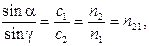(3.3)
где n 21– относительный показатель преломления второй среды относительно первой.
Из двух сред, имеющих различные показатели преломления, среда с меньшим показателем называется оптически менее плотной, а среда с большим показателем – оптически более плотной.
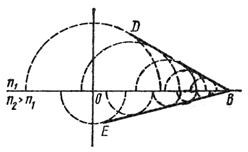
Если свет проходит из оптически более плотной среды в оптически менее плотную среду, например, из стекла в воду, то, согласно формуле (3.3), угол падения αбудет меньше угла преломления γ (рис. 3.3 а). Поэтому при некотором угле падения (α = А) угол преломления окажется равным 90°, т. е. преломленный луч будет скользить вдоль границы раздела сред, не входя во вторую среду (рис. 3.3б). Угол А называется предельным углом падения. При α > А свет полностью отражается в первую среду (рис. 3.3 в). Это явление называется полным внутренним отражением света.
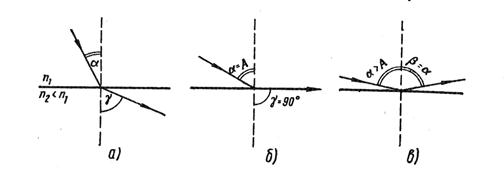
Рис. 3.3
Согласно формуле (3.3)
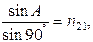откуда sin A = n 21.
|
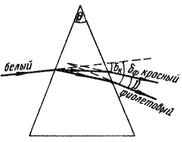
Угол отклонения δ зависит от преломляющего угла Ө и показателя преломления призмы n. Эта зависимость легко устанавливается для призмы с малым преломляющим углом Ө в случаях малого угла падения α.Для призмы находящейся в воздухе
δ = (n – 1) Ө. (3.4)
