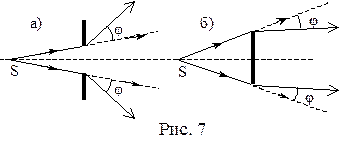 Закон прямолинейного распространения света известен с давних времен. Об этом, в частности, свидетельствует и наш повседневный опыт. Кто из нас не наблюдал, как при освещении непрозрачных предметов за ними образуется тень, т.е. область, куда свет не заходит. Однако обнаруживается, что волны на краях препятствий не подчиняться закону прямолинейного распространения. Они могут проникать в область геометрической тени (рис.7). Явление отклонения световых волн от прямолинейного распространения при прохождении света мимо края препятствия получило название дифракции света.
Закон прямолинейного распространения света известен с давних времен. Об этом, в частности, свидетельствует и наш повседневный опыт. Кто из нас не наблюдал, как при освещении непрозрачных предметов за ними образуется тень, т.е. область, куда свет не заходит. Однако обнаруживается, что волны на краях препятствий не подчиняться закону прямолинейного распространения. Они могут проникать в область геометрической тени (рис.7). Явление отклонения световых волн от прямолинейного распространения при прохождении света мимо края препятствия получило название дифракции света.
Объяснить явление дифракции можно исходя из принципа Гюйгенса-Френеля. Этот принцип представляет собой правило, объясняющее, как, исходя из положения волнового фронта в данный момент, найти новое положение волнового фронта в последующий момент времени.
Гюйгенс предложил рассматривать каждую точку среды, которой достигла волна, как источник вторичных сферических волн, распространяющихся по всем направлениям со скоростью, присущей данной среде. Поверхность, огибающая вторичные волны, представляет собой фронт волны в данный момент времени.
Изложенное правило позволяет определить направление распространения волнового фронта, но не затрагивает вопроса о количественном распределении энергии дифрагировавшей волны. Этот недостаток был устранен Френелем, который дополнил изложенный принцип следующим положением: вторичные сферические волны являются когерентными и колебания в любой точке пространства, которой вторичные волны достигнут в момент времени t, представляют собой результат интерференции этих вторичных волн. Т.о., правило распространения огибающей поверхности было заменено расчетом взаимной интерференции вторичных волн.
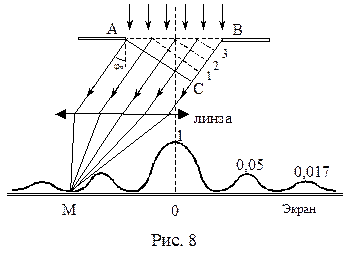 В качестве примера практического использования принципа Гюйгенса–Френеля рассмотрим дифракцию плоской волны (дифракцию Фраунгофера) на щели (рис.8). Выберем за щелью произвольное направление распространения света, которое образует с направлением падающего пучка угол φк (угол дифракции). Проведем АС перпендикулярно выбранному направлению дифракции. Разобьем ВС на отрезки длиной l/2. Параллельно АС через точки разбиения (1, 2, 3) проведем линии, которые разделят открытую часть волновой поверхности АВ на участки равной ширины – зоны Френеля,параллельные краям щели. По построению АМ = СМ, а ∆ – разность хода лучей от краев зон Френеля равна l/2. Это означает, что волны, идущие от двух соседних зон при наложении погасят друг друга. Т.о., если на открытой части волновой поверхности для данного направления наблюдения уложится целое четное число зон Френеля, то для данного направления будет наблюдаться min интенсивности, т.к. зоны попарно друг друга погасят. Если число зон Френеля целое и нечетное, то в этом направлении будет наблюдаться max.
В качестве примера практического использования принципа Гюйгенса–Френеля рассмотрим дифракцию плоской волны (дифракцию Фраунгофера) на щели (рис.8). Выберем за щелью произвольное направление распространения света, которое образует с направлением падающего пучка угол φк (угол дифракции). Проведем АС перпендикулярно выбранному направлению дифракции. Разобьем ВС на отрезки длиной l/2. Параллельно АС через точки разбиения (1, 2, 3) проведем линии, которые разделят открытую часть волновой поверхности АВ на участки равной ширины – зоны Френеля,параллельные краям щели. По построению АМ = СМ, а ∆ – разность хода лучей от краев зон Френеля равна l/2. Это означает, что волны, идущие от двух соседних зон при наложении погасят друг друга. Т.о., если на открытой части волновой поверхности для данного направления наблюдения уложится целое четное число зон Френеля, то для данного направления будет наблюдаться min интенсивности, т.к. зоны попарно друг друга погасят. Если число зон Френеля целое и нечетное, то в этом направлении будет наблюдаться max.
Определим эти направления. Из построения видно, что ширина одной зоны Френеля – l0 будет:
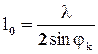 ,
,
а число зон, укладывающихся в щели АВ шириной b:
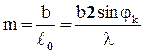 .
.
Т.к. минимум наблюдается при m = 2k, то условие минимума –
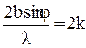 , откуда bsinφ = 2kl/2. (18)
, откуда bsinφ = 2kl/2. (18)
При m = (2k +1) наблюдается максимум и условие максимума –
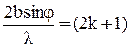 , откуда bsinφ = (2k+1)l/2. (19)
, откуда bsinφ = (2k+1)l/2. (19)
Т.о., на экране за щелью мы будем наблюдать систему чередующихся светлых и темных полос, симметричных относительно середины щели. Отметим, что для направлений, в которых на открытую часть волнового фронта уложится не целое число зон Френеля, интенсивность будет иметь некоторое промежуточное значение. Это значит, что переходы от max к min и от min к max будут плавными.
Дифракционный спектр может быть использован для изучения состава излучения. Однако при дифракции на щели энергия, переносимая в направлении max невелика и наблюдения затруднены.
4.4 ЯВЛЕНИЕ ПОЛЯРИЗАЦИИ
 В пучке естественного света результирующий световой вектор
В пучке естественного света результирующий световой вектор 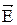 быстро и беспорядочно меняет направление своих колебаний (рис.9а). Однако при определенных условиях можно получить пучок света, в котором колебания светового вектора
быстро и беспорядочно меняет направление своих колебаний (рис.9а). Однако при определенных условиях можно получить пучок света, в котором колебания светового вектора 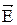 будут совершаться только вдоль одного единственного направления. Такой пучок называется плоско- или линейно поляризованным.
будут совершаться только вдоль одного единственного направления. Такой пучок называется плоско- или линейно поляризованным.
Плоскость, проходящая через вектор 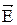 и направление распространения волны, т.е. через вектор скорости
и направление распространения волны, т.е. через вектор скорости 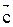 получила название плоскости поляризации пучка (рис. 9б).
получила название плоскости поляризации пучка (рис. 9б).
Световой пучок, в котором колебания 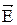 вдоль какого-то одного направления преобладают над колебаниями в других направлениях, называется частично поляризованным.
вдоль какого-то одного направления преобладают над колебаниями в других направлениях, называется частично поляризованным.
Поляризация достаточно распространенное явление природы. Однако мы этого не замечаем, т. к. глаз человека не в состоянии отличить поляризованный свет от неполяризованного. По этой причине поляризацию света и явления с ней связанные, можно наблюдать только с помощью специальных приборов, которые называются поляризаторами. Эти устройства свободно пропускают колебания, параллельные одной определенной плоскости, которую можно выделить в каждом поляризаторе, и не пропускают колебания перпендикулярные этой плоскости. Эту плоскость мы будем называть главной плоскостью поляризатора.
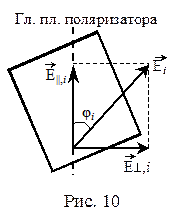 Пусть направление колебаний напряжённости электрического поля i -ой волны образует с главной плоскостью поляризации угол φ i (рис.10). Тогда составляющая
Пусть направление колебаний напряжённости электрического поля i -ой волны образует с главной плоскостью поляризации угол φ i (рис.10). Тогда составляющая 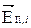 , прошедшая через поляризатор, имеет амплитуду:
, прошедшая через поляризатор, имеет амплитуду: 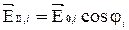 . Так как в пучке естественного света все значения φ i равновероятны, а интенсивность I ~ Е2, то доля интенсивности, прошедшей через поляризатор будет равна доле не прошедшей, т. е.
. Так как в пучке естественного света все значения φ i равновероятны, а интенсивность I ~ Е2, то доля интенсивности, прошедшей через поляризатор будет равна доле не прошедшей, т. е.
I = Σ · I0, i · cos2φi = I0/2. (20)
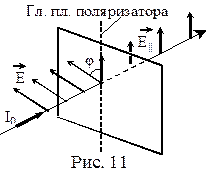 Рассмотрим случай, когда на поляризатор падает плоскополяризованное излучение (рис.11). Ясно, что если плоскость поляризации пучка параллельна главной плоскости поляризатора, то пучок проходит полностью, а если перпендикулярна, то не проходит совсем.
Рассмотрим случай, когда на поляризатор падает плоскополяризованное излучение (рис.11). Ясно, что если плоскость поляризации пучка параллельна главной плоскости поляризатора, то пучок проходит полностью, а если перпендикулярна, то не проходит совсем.
В произвольном случае (для одной волны) через поляризатор пройдет составляющая колебаний с амплитудой 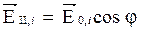 . Интенсивность поляризованного пучка света, прошедшего через поляризатор определяется законом Малюса. Учитывая, что для всех волн пучка угол φ имеет одно и то же значение, для интенсивности получим:
. Интенсивность поляризованного пучка света, прошедшего через поляризатор определяется законом Малюса. Учитывая, что для всех волн пучка угол φ имеет одно и то же значение, для интенсивности получим:
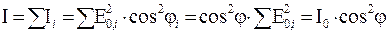 . (21)
. (21)
4.5 ЯВЛЕНИЯ, ПРИВОДЯЩИЕ К ПОЛЯРИЗАЦИИ СВЕТА
ЯВЛЕНИЕ ДВУЛУЧЕПРЕЛОМЛЕНИЯ
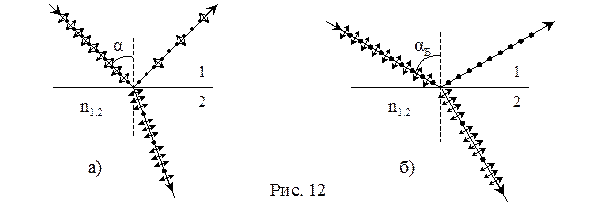
Как показывает опыт, явление частичной, а при определенных условиях и полной поляризации, имеет место при отражении, преломлении, рассеянии и поглощении естественного света. Например: при падении света на границу раздела двух диэлектриков под углом не равным нулю отражённый и преломленный лучи оказываются частично поляризованными. Причём, в отражённом луче преобладают колебания, перпендикулярные плоскости падения, а в преломлённом – параллельные ей (рис.12а). Степень поляризации в этом случае зависит от угла падения α. При угле падения αБ, удовлетворяющему условию:
 , (22)
, (22)
отражённый луч оказывается полностью поляризованным, а преломлённый достигает максимума поляризации (рис.12б). Это закон Брюстера (n1,2 – показатель преломления среды 2 относительно среды 1). Можно показать, что при выполнении закона Брюстера, отраженный и преломленный лучи взаимноперпендикулярны.
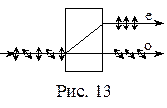 Для поляризации света обычно используют явление двойного лучепреломления. Явление состоит в том, что при преломлении света на границе анизотропной среды (кристаллы исландского шпата – СаСО3, турмалина, кварца и др.) наблюдается раздвоение преломленного светового пучка (рис.13). Это происходит вследствие зависимости скорости световых волн, а значит и показателя преломления, от направления колебаний вектора
Для поляризации света обычно используют явление двойного лучепреломления. Явление состоит в том, что при преломлении света на границе анизотропной среды (кристаллы исландского шпата – СаСО3, турмалина, кварца и др.) наблюдается раздвоение преломленного светового пучка (рис.13). Это происходит вследствие зависимости скорости световых волн, а значит и показателя преломления, от направления колебаний вектора 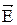 . Для одного луча выполняются законы преломления, и он называется обыкновенным – о. Для другого они не выполняются. Этот луч называется необыкновенным – е. Необыкновенный луч может не лежать в плоскости падения, а отношение синуса угла падения к синусу угла преломления (sinα/sinβ) для него не постоянно. Оно зависит от значения угла падения α. Оба луча являются полностью поляризованными.
. Для одного луча выполняются законы преломления, и он называется обыкновенным – о. Для другого они не выполняются. Этот луч называется необыкновенным – е. Необыкновенный луч может не лежать в плоскости падения, а отношение синуса угла падения к синусу угла преломления (sinα/sinβ) для него не постоянно. Оно зависит от значения угла падения α. Оба луча являются полностью поляризованными.
В двулучепреломляющих кристаллах существуют направления, для которых скорости распространения обыкновенного и необыкновенного лучей одинаковы 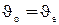 . Для этих направлений, которые называются оптическими осями кристалла, явление двойного лучепреломления не наблюдается. Плоскости, проходящие через оптические оси и падающий луч, являются главными плоскостями таких кристаллов. Колебания вектора
. Для этих направлений, которые называются оптическими осями кристалла, явление двойного лучепреломления не наблюдается. Плоскости, проходящие через оптические оси и падающий луч, являются главными плоскостями таких кристаллов. Колебания вектора 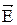 обыкновенного луча перпендикулярны главной плоскости, а необыкновенного – лежат в этой плоскости.
обыкновенного луча перпендикулярны главной плоскости, а необыкновенного – лежат в этой плоскости.
Самостоятельно двулучепреломляющие кристаллы как поляризаторы не используются, т. к. обыкновенный и необыкновенный лучи пространственно расходятся очень мало. Из таких кристаллов изготавливают специальные поляризационные призмы – николи. Николь представляет собой параллелепипед, разрезанный по диагонали и склеенный канадским бальзамом (смола пихты) с nо > nбальзама > nе (рис.14). Подбирая соответствующим образом огранку николя, добиваются полного отражения обыкновенного луча от границы кристалл – канадский бальзам (рис.14).
В некоторых двулучепреломляющих кристаллах один из лучей испытывает аномально большое поглощение. Это явление получило название – дихроизм. Сильным дихроизмом в видимых лучах обладают кристаллы турмалина. Поляризаторы на основе этого явления представляют собой прозрачную полимерную пленку толщиной около 0,1 мм, в которую введено большое количество одинаково ориентированных кристалликов, например, сульфата йодистого хинина – герапатита. Такие поляризаторы называются поляроиды.
4.6 ОПТИЧЕСКАЯ АКТИВНОСТЬ ВЕЩЕСТВ
При прохождении плоскополяризованного света через некоторые вещества наблюдается вращение плоскости поляризации вокруг направления распространения луча. Вещества, обладающие такой способностью, называются оптически активными (кварц, скипидар, никотин, водные растворы сахара и винной кислоты и др.). Это явление обусловлено особенностями структуры молекул этих веществ. Различают левовращающие и правовращающие оптически активные вещества.
В общем случае, для всех оптически активных веществ угол поворота Δφ плоскости поляризации для данной длины волны прямопропорционален толщине слоя l, через который проходит поляризованный пучок света:
Δφ = α · l. (23)
Коэффициент α называется постоянной вращения или вращательной способностью вещества. Значение α зависит от температуры, природы вещества и длины волны излучения λ. Так, например, для кварца при λ = 0,5890 мкм – α = 21,7 град/мм, а если λ = 0,4047 мкм – α = 48,9 град/мм. Зависимость α = f (λ) получила название дисперсии оптической активности. Для растворов оптически активных веществ вращательная способность прямопропорциональна концентрации вещества с – α = [α0] c. В этом случае:
Δφ = [α0] c l. (24)
Коэффициент [α0] называется удельным вращением. Его значение зависит от природы оптически активного вещества, длины волны, температуры и свойств растворителя.
Соотношение (24) лежит в основе концентрационной поляриметрии – метода измерения концентрации растворенных веществ. В медицине этот метод используется для определения содержания сахара в моче. Соответствующие приборы для измерения концентрации называются поляриметрами.
Явление поляризации нашло применение и в других практических случаях: в поляризационной микроскопии, исследовании структурных превращений веществ, молекулярной биофизике и т. д.
 2014-02-09
2014-02-09 9298
9298